Практическая работ4. Практическая работа 60 Расчет надежности сложных систем
 Скачать 85.96 Kb. Скачать 85.96 Kb.
|
|
Практическая работа № 60 «Расчет надежности сложных систем» Цель: научить студентов определять показатели надежности объектов, представляющих сложные системы. Задачи обучения: ознакомить с методами резервирования; привить навыки построения структуры сложной системы; научить рассчитывать показатели надежности системы без резервирования; научить рассчитывать показатели надежности системы с резервированием. Задания и методические указания к их выполнению (алгоритм, форма, сроки отчетности, критерии оценивания): Пример 6.1. Определить вероятность безотказной работы и вероятность отказа основной системы, состоящей из пяти элементов, если вероятности безотказной работы элементов равны P1(t)=0,98, P2(t)=0,97, P3(t)=0,99, P4(t)=0,98, P5(t)=0,96. Решение: вероятность безотказной работы системыPс(t) определяем по формуле (3.1): 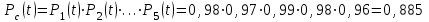 , , вероятность отказа Qc(t) системы определяется по формуле (3.5): 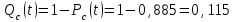 . . Ответ: 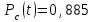 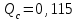 . .Пример 6.2. Определить среднее время безотказной работы системы, если система состоит из трех элементов, среднее время безотказной работы которых равны 400, 200 и 500 часов, закон распределения – экспоненциальный. Решение: Определим интенсивности отказов элементов по формуле (2.11) 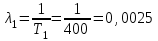 1/час; 1/час; 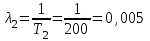 1/час; 1/час; 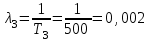 1/час. 1/час.Интенсивность отказа системы определяем по формуле (3.7) 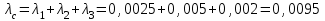 1/час. 1/час.Наработку до отказа системы рассчитаем по формуле (3.8) 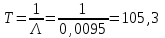 час. час.Ответ: 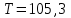 час. час. Пример 6.3. Система состоит из трех элементов, вероятность безотказной работы которых в течении 100 часов равны Р1(100) = 0,95; Р1(100) = 0,99; Р3(100) = 0,97. Найти среднее время безотказной работы системы, закон распределения – экспоненциальный. Решение: Определим вероятность безотказной работы системы 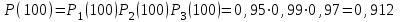 . .Выразим интенсивность отказа системы из формулы (3.6) 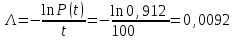 . .Среднее время безотказной работы системы определяем по формуле (3.8) 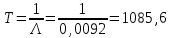 час. час.Ответ: 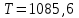 час. час.Пример 6.4. Система состоит из 6000 элементов, средняя интенсивность отказов которых ср=5,4*10-7 1/час. Определить вероятность безотказной работы, вероятность отказа, плотность вероятности времени безотказной работы за время 100 часов, и среднее время безотказной работы. Решение: Интенсивность отказов системы определяем по формуле (3.7) 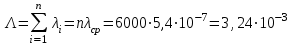 . . Вероятность безотказной работы рассчитаем по формуле (3.6) 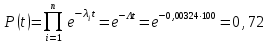 , , Вероятность отказа системы 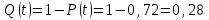 Наработка до отказа системы 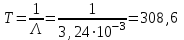 час. час.Плотность вероятности времени безотказной работы 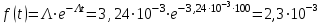 1/час. 1/час.Пример 6.6. Система состоит из трех элементов с равной вероятностью безотказной работы равной 0,9. Определить вероятности безотказной работы системы при различных вариантах резервирования. Решение: а) расчет показателей надежности системы без резервирования: Вероятность безотказной работы системы без резервирования определяется по формуле (2.1): 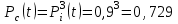 , , Вероятность отказа системы без резервирования определяем по формуле (2.5) 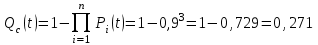 . .б) расчет показателей надежности системы при общем резервировании: Структурная схема системы с общим резервированием показана на рисунке 3.3. 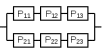 Рисунок 6.1 – Схема системы с общим резервирование: Р11, Р12, Р13 – вероятности безотказной работы элементов основной системы; Р21, Р22, Р23 – вероятности безотказной работы элементов резервной системы Вероятность отказа системы с общим резервированием определяется по формуле (2.6): 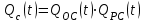 , , где QOC(t) – вероятность отказа основной системы; QPC(t) – вероятность отказа резервной системы. Вероятность отказа основной системы определяем по формуле (2.5) 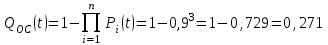 . .Вероятность отказа резервной системы равна 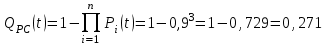 . .Вероятность отказа системы: 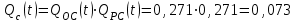 . .Вероятность безотказной системы с общим резервированием определяем по формуле (2.8) 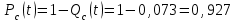 . .в) расчет показателей надежности системы при поэлементном резервировании: Структурная схема системы с поэлементным резервированием показана на рисунке 3.4. 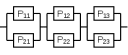 Рисунок 6.2 – Схема системы с поэлементным резервирование: Р11, Р12, Р13 – вероятности безотказной работы основных элементов; Р21, Р22, Р23 – вероятности безотказной работы резервных элементов Вероятность безотказной работы системы с поэлементным резервированием определяем по формуле (2.6): 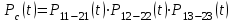 , , где Р11-21(t) – вероятность безотказной работы группы из первого основного и резервного элементов; Р12-22(t) – вероятность безотказной работы группы из второго основного и резервного элементов; Р13-23(t) – вероятность безотказной работы группы из третьего основного и резервного элементов. 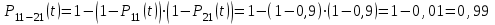 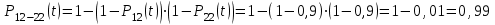 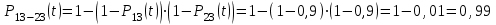 Вероятность безотказной работы системы с поэлементным резервированием: 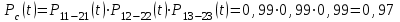 , , Так как вероятности безотказной работы групп элементов близки к единице, можно было воспользоваться формулой для приближенного расчета (2.3): 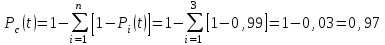 . . Вероятность отказа основной системы определяем по формуле (2.5) 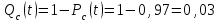 . .Ответ: для системы без резервирования: 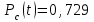 , ,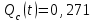 ; для системы с общим резервированием ; для системы с общим резервированием 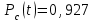 , , 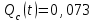 ; для системы с поэлементным резервированием: ; для системы с поэлементным резервированием: 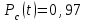 , , 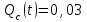 . Таким образом, максимальная надежность достигается при поэлементном резервировании. . Таким образом, максимальная надежность достигается при поэлементном резервировании.Задания для самостоятельной работы студентов Задача 7.1. Определить вероятность безотказной работы системы, состоящей из 500 элементов, если вероятность безотказной работы каждого элемента в течение времени tравна P(t) = 0,998. Задача 7.2. Вероятность безотказной работы системы, состоящей из 150 равнонадежных элементов, в течение времени t равна Рc(t)=0,95. Найти вероятность безотказной работы элемента. Задача 7.3. Блок управления состоит из 5000 элементов, средняя интенсивность отказов которых равна 2,3·10-6 1/час. Определить вероятность безотказной работы в течении t = 100 час и среднее время безотказной работы. Задача 7.4. Система состоит из пяти элементов, среднее время безотказной работы которых равно: Т1=104 час; Т2=200 час; Т3=185 час; Т4=350 час; Т5=620 час. Показатели распределены по экспоненциальному закону. Определить среднее время безотказной работы системы. Задача 7.5. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени t = 50 час равна: P1(50)=0,98; P2(50)=0,99; P3(50)=0,998; P4(50)=0,975; P5(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора. Задача 7.6. Установка состоит из 3000 элементов, средняя интенсивность отказов которых 3,8·10-6 1/час. Определить вероятность отказа установки в течении t = 300 час и среднее время безотказной работы аппаратуры. Задача 7.7. Объект состоит из 200000 элементов, средняя интенсивность отказов которых 0,2·10-6 1/час. Определить вероятность безотказной работы системы в течение 240 часов и среднее время безотказной работы. Задача 7.8. Прибор состоит из 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t , которая равна: P1(t)=0,98; P2(t)=0,99; P3(t)=0,998; P4(t)=0,975; P5(t)=0,985. Необходимо определить вероятность безотказной работы прибора. Задача 7.9. Определить количество равнонадежных резервных элементов с вероятностью безотказной работы Pi(t)=0,9,необходимых для того, чтобы обеспечить вероятность безотказной работы системы равную Pс(t)=0,99. Задача 7.10. Система состоит из четырех элементов, имеющих интенсивность отказов равную λ1 = 2,7·10-7 1/час, λ2 = 3,2·10-7 1/час, λ3 = 2,1·10-7 1/час, λ4 = 4,3·10-7 1/час. Изобразить структурную схему системы и определить вероятность безотказной работы и вероятность отказа в течение 60 часов при общем резервировании системы. Задача 7.11. Система состоит из четырех элементов, имеющих интенсивность отказов равную λ1 = 2,7·10-7 1/час, λ2 = 3,2·10-7 1/час, λ3 = 2,1·10-7 1/час, λ4 = 4,3·10-7 1/час. Изобразить структурную схему системы и определить вероятность безотказной работы и вероятность отказа в течение 60 часов при Задача 7.16 Система состоит из трех элементов с вероятностью безотказной работы равной P1(t)=0,9, P2(t)=0,92, P3(t)=0,87. Определить время безотказной работы системы при поэлементном резервировании. Контрольные вопросы: Дайте характеристику сложной системы. Как рассчитываются показатели надежности системы без резервирования (основной системы)? Что такое резервирование? Какие используются виды резервирования? Дайте определение и характеристику общему и поэлементному резервированию. Дайте определение и характеристику постоянному резервированию и резервированию замещением. Дайте определение и характеристику резервированию с восстановлением и без восстановления. Вероятность отказа основной системы определяем по формуле (2.5) |
