Практическая. Практическая работа ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Практическая работа однофакторный дисперсионный анализ

• Название: Практическая работа однофакторный дисперсионный анализ
• Анкор: Практическая
• Дата: 31.03.2023
• Размер: 125.07 Kb.
• Имя файла: Практическая работа ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ.docx
• Тип: Практическая работа; #1028099

Практическая работа

ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Цель работы: Научиться выявлять влияние отдельного фактора на пара-метр оптимизации.

Задачи работы:

1. Выбрать задание, включающее серию выборок с разными значениями фактора, оказывающим влияние на параметры технологического процесса.

2. Рассчитать внутригрупповую и межгрупповую суммы квадратов отклонений и соответствующие им дисперсии.

3. Провести проверку гипотезы об отсутствии влияния фактора на параметр оптимизации с помощью критерия Фишера.

4. Сделать вывод о влиянии фактора (или об отсутствии такового) на параметр оптимизации.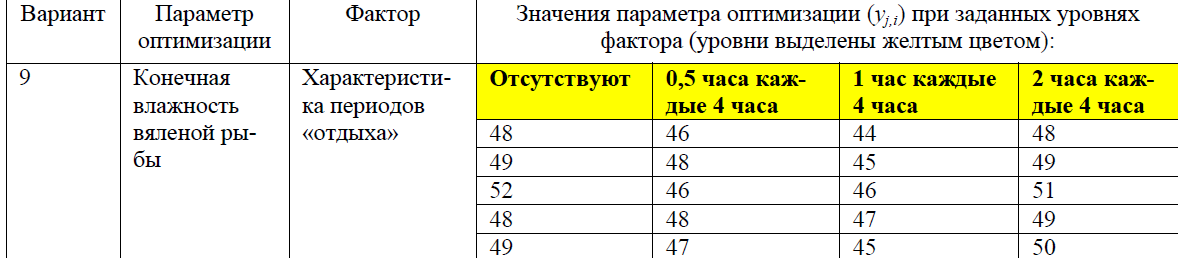



Находим групповые средние:

N	П1	П2	П3	П4
1	48	46	44	48
2	49	48	45	49
3	52	46	46	51
4	48	48	47	49
5	49	47	45	50
∑	246	235	227	247
xср	49.2	47	45.4	49.4

Обозначим р - количество уровней фактора (р=4). Число измерений на каждом уровне одинаково и равно q=5.

В последней строке помещены групповые средние для каждого уровня фактора.
Общая средняя вычисляется по формуле:


Для расчета Sобщ по формуле (4) составляем таблицу 2 квадратов вариант:

N	П21	П22	П23	П24
1	2304	2116	1936	2304
2	2401	2304	2025	2401
3	2704	2116	2116	2601
4	2304	2304	2209	2401
5	2401	2209	2025	2500
∑	12114	11049	10311	12207

S_общ = 12114 + 11049 + 10311 + 12207 - 5 • 4 • 47.75² = 79.75

Находим S_ф по формуле (5):

S_ф = 5(49.2² + 47² + 45.4² + 49.4² - 4 • 47.75²) = 54.55

Получаем S_ост: S_ост = S_общ - S_ф = 79.75 - 54.55 = 25.2

Определяем факторную дисперсию:


и остаточную дисперсию:


Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.

Оценка факторной дисперсии больше оценки остаточной дисперсии, поэтому можно сразу утверждать не справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.

Иначе говоря, в данном примере фактор Ф оказывает существенное влияния на случайную величину.

Проверим нулевую гипотезу H₀: равенство средних значений х.

Находим f_набл.


Для уровня значимости α=0.05, чисел степеней свободы 3 и 16 находим f_кр из таблицы распределения Фишера-Снедекора.

f_кр(0.05; 3; 16) = 3.24

В связи с тем, что f_набл > f_кр, нулевую гипотезу о существенном влиянии фактора на результаты экспериментов принимаем (нулевую гипотезу о равенстве групповых средних отвергаем). Другими словами, групповые средние в целом различаются значимо.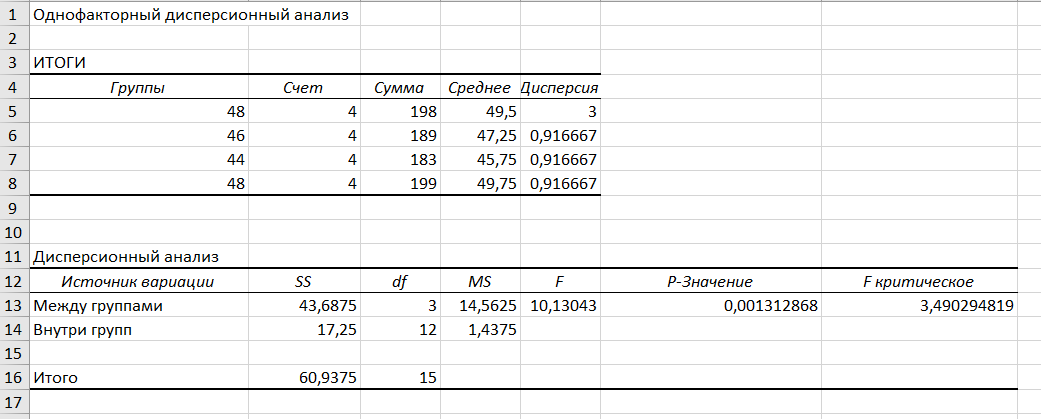