Основы теории выбора средств реализации информационно-вычислительных систем. Практическая работа по дисциплине Основы теории выбора средств реализации информационновычислительных систем по теме Разработка цифрового автомата

• Название: Практическая работа по дисциплине Основы теории выбора средств реализации информационновычислительных систем по теме Разработка цифрового автомата
• Анкор: Основы теории выбора средств реализации информационно-вычислительных систем
• Дата: 25.04.2022
• Размер: 367.64 Kb.
• Имя файла: Variant_21_SemenovEP_19iv1bzi.docx
• Тип: Практическая работа; #494974
• страница: 1 из 3

М ИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Пензенский государственный технологический университет»

(ПензГТУ)

Кафедра «Вычислительные машины и системы»
Практическая работа
по дисциплине «Основы теории выбора средств реализации информационно-вычислительных систем»

по теме «Разработка цифрового автомата»

Вариант №21

Выполнил:

студент группы 19ИВ1бзи

Семенов Е.П.

Проверил:

Доцент каф. “ВМиС”, к.т.н. Мартышкин А.И.

Пенза 2020

Задание №1

1. По заданной совмещенной таблице переходов и выходов автомата Мили построить:

1. 
   прямую таблицу переходов;
   
2. 
   обратную таблицу переходов;
   
3. 
   граф;
   
4. 
   записать СКУ и СВФ.
   

Вариант 21

	a1	a2	a3	a4
z1	a1/w4	a4/w1	a1/w2	a2/w3
z2	a3/w5	a4/w5	a4/w1	a3/w5

Решение.

1. 
   Составим прямую таблицу переходов автомата Мили (табл. 1.1), в которой последовательно перечислим все переходы сначала из первого состояния, затем из второго и т.д.
   

Таблица 1.1. Прямая таблица переходов автомата Мили

am(t)	zf(t)	as(t+1)	wg(t)
a1	z1	a1	w4
	z2	a3	w5
a2	z1	a4	w1
	z2	a4	w5
a3	z1	a1	w2
	z2	a4	w1
a4	z1	a2	w3
	z2	a3	w5

2. 
   Составим обратную таблицу переходов автомата Мили (табл. 1.2), в которой сначала запишем все переходы в первое состояние, затем во второе и т.д.
   

Таблица 1.2. Обратная таблица переходов автомата Мили

am(t)	zf(t)	as(t+1)	wg (t)
a1	z1	a1	w4
a3	z1		w2
a4	z1	a2	w3
a1	z2	a3	w5
a4	z2		w5
a2	z1	a4	w1
a2	z2		w5
a3	z2		w1

3. 
   Построим граф автомата Мили (рис. 1.1), вершины которого соответствуют состояниям, а дуги – переходам между ними. В начале каждой дуги запишем входной сигнал z_fZ, вызывающий переход: a_s= (a_m, z_f), а в конце дуги – выходной сигнал w_gW, формируемый на переходе.
   

Рис. 1.1. Граф автомата Мили

4. 
   Составим СКУ и СВФ, которые определяют функции переходов и выходов автомата соответственно.
   

Система канонических уравнений (СКУ):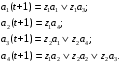


Система выходных функций (СВФ):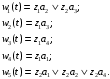

2. Преобразовать заданный в п.1 автомат Мили в эквивалентный ему автомат Мура. Для полученного автомата Мура построить:

1. 
   отмеченную таблицу переходов;
   
2. 
   прямую таблицу переходов;
   
3. 
   обратную таблицу переходов;
   
4. 
   граф;
   
5. 
   СКУ и СВФ;
   

Решение.

Для автомата Мура: Z ^/ = Z = {z₁, z₂};

W ^/ = W = {w₁, w₂, w₃, w₄, w₅}.

Построим множество А^/. Для этого найдем множество пар, порождаемых каждым состоянием автомата Мили S. Каждую пару обозначим символами b₁, b₂, ...:

A₁ = {(a₁, w₂), (a₁, w₄)} = {b₁, b₂};

A₂ = {(a₂, w₃)} = {b₃};

A₃ = {(a₃, w₅)} = {b₄};

A₄ = {(a₄, w₁), (a₄, w₅)} = {b₅, b₆}.

A ^/={b₁, b₂, b₃, b₄, b₅, b₆}.

Для определения функции ^/ с каждым состоянием вида (a_s, w_g), представляющим собой пару, отождествим выходной сигнал, являющийся вторым элементом этой пары:

 ^/(b₁) = w₂;

 ^/(b₂) = w₄;

 ^/(b₃) = w₃;

 ^/(b₄) = ^/(b₆) = w₅;

 ^/(b₅) = w₁.

1. 
   Для полученного автомата Мура построим отмеченную таблицу переходов (табл. 1.3).
   

Таблица 1.3. Отмеченная таблица переходов S ^/

W /	w2	w4	w3	w5	w1	w5
A /	b1	b2	b3	b4	b5	b6
z1	b2	b2	b5	b1	b3	b3
z2	b4	b4	b6	b5	b4	b4

2. 
   Составим прямую таблицу переходов автомата Мура (табл. 1.4), в которой последовательно перечислим все переходы сначала из первого состояния, затем из второго и т.д.
   

Таблица 1.4. Прямая таблица переходов автомата Мура

bm(t)	wg(t)	zf(t)	bs(t+1)
b1	w2	z1	b2
		z2	b4
b2	w4	z1	b2
		z2	b4
b3	w3	z1	b5
		z2	b6
b4	w5	z1	b1
		z2	b5
b5	w1	z1	b3
		z2	b4
b6	w5	z1	b3
		z2	b4

3. 
   Составим обратную таблицу переходов автомата Мура (табл. 1.5), в которой сначала запишем все переходы в первое состояние, затем во второе и т.д.
   

Таблица 1.5. Обратная таблица переходов автомата Мура

bm(t)	zf(t)	bs(t+1)	wg(t+1)
b4	z1	b1	w2
b1	z1	b2	w4
b2	z1
b5	z1	b3	w3
b6	z1
b1	z2	b4	w5
b2	z2
b5	z2
b6	z2
b3	z1	b5	w1
b4	z2
b3	z2	b6	w5

4. 
   Построим граф автомата Мура (рис. 1.2), вершины которого соответствуют состояниям, а дуги – переходам между ними. В начале каждой дуги запишем входной сигнал z_fZ, вызывающий переход: a_s= (a_m, z_f), а выходной сигнал w_gW укажем рядом с вершиной, отмеченной состоянием a_m, в котором он формируется.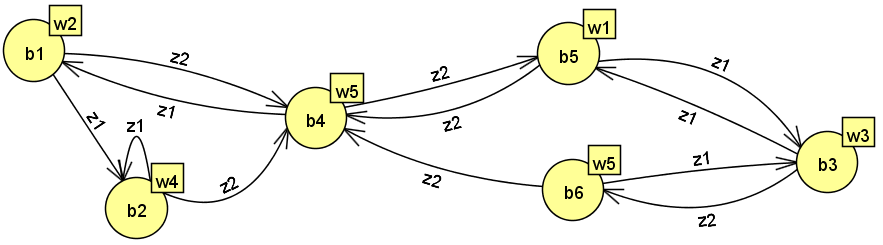
   

Рис. 1.2. Граф автомата Мура

5. 
   Составим СКУ и СВФ, которые определяют функции переходов и выходов автомата соответственно.
   

Система канонических уравнений (СКУ):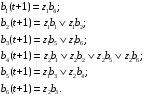



Система выходных функций (СВФ):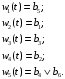

3. Преобразовать полученный в п.2 автомат Мура в эквивалентный ему автомат Мили и выполнить его минимизацию.
Решение.

Для автомата Мили: Z ^/ = Z = {z₁, z₂}; W ^/ = W = {w₁w₂, w₃, w₄, w₅};

B ^/ =B = {b₁, b₂, b₃, b₄, b₅, b₆}; ^/= ;b₁^/ = b₁.

На рис. 1.3 приведен граф автомата Мура S, эквивалентного автомату Мили S^/. Для преобразования выходной сигнал (w_g), записанный рядом с вершиной (b_s), переносим на все дуги, входящие в эту вершину.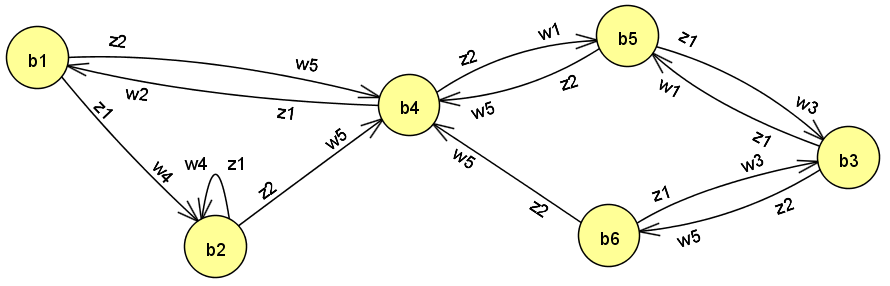







Рис. 1.3. Автомата Мили S^/, эквивалентный автомату МураS
Табл. 1.6 − совмещенная таблица переходов и выходов автомата Мили. Для её получения вместе с состояниями перехода a_s запишем отмечающие их выходные сигналы w_g.

Таблица 1.3. Отмеченная таблица переходов и выходов автомата Мура W w2 w4 w3 w5 w1 w5 B b1 b2 b3 b4 b5 b6 z1 b2 b2 b5 b1 b3 b3 z2 b4 b4 b6 b5 b4 b4

Таблица 1.6. Совмещенная таблица переходов и выходов автомата Мили B / b1 b2 b3 b4 b5 b6 z1 b2/ w4 b2/ w4 b5/ w1 b1/ w2 b3/ w3 b3/ w3 z2 b4/ w5 b4/ w5 b6/ w5 b5/ w1 b4/ w5 b4/ w5

Выполним минимизацию полученного автомата Мили с помощью треугольной таблицы.

По табл. 1.6 составляется треугольная таблица (табл. 1.7), столбцы и строки которой сопоставляются с состояниями автомата. Для упрощения записи в этой таблице вместо b_i будем писать i.

В треугольной таблице на пересечении строки mи столбца s поставим:

• 
  X (крест), если состояния b_m и b_s имеют разные выходные сигналы;
  
• 
  множество всех пар состояний, следующих за парой (b_m, b_s) и отличных от неё, эквивалентность которых необходима для эквивалентности пары (b_m, b_s).
  
• 
  V (птичка), если за парой (b_m,b_s), не следуют пары, отличные от (b_m, b_s).
  

Таблица 1.7. Треугольная таблица для автомата S

2 V 3 X X 4 X X X 5 X X X X 6 X X X X V 1 2 3 4 5

В результате получим эквивалентные пары состояний: 12, 56.
Выполним замену состояний b_i ≡ c_i, при этом учтем, что каждый класс эквивалентности {b₁, b₂} и {b₅, b₆} можно заменить одним состоянием:

{b₁, b₂} = c₁, b₃ = c₂, b₄ = c₃, {b₅, b₆} = c₄.

Построим совмещенную таблицу переходов и выходов минимального автомата Мили (табл. 1.8).
Таблица 1.8. Совмещенная таблица переходов и выходов

минимального автомата Мили

B	{b1, b2}	b3	b4	{b5, b6}
z1	b2/ w4	b5/ w1	b1/ w2	b3/ w3
z2	b4/ w5	b6/ w5	b5/ w1	b4/ w5

С	с1	с2	с3	с4
z1	c1/ w4	c4/ w1	c1/ w2	c2/ w3
z2	c3/ w5	c4/ w5	c4/ w1	c3/ w5