Основы теории выбора средств реализации информационно-вычислительных систем. Практическая работа по дисциплине Основы теории выбора средств реализации информационновычислительных систем по теме Разработка цифрового автомата
 Скачать 367.64 Kb. Скачать 367.64 Kb.
|
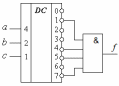
Задание №3Тема: Синтез комбинационных схем на основе дешифраторов1. Реализовать функцию трех переменных на основе дешифратора двумя способами. Вариант 21. Y = f (a, b, c) = ( 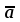 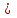 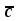 )( )(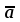 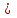 b)(b b)(b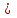 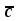 ). ).Решение. Составим таблицу истинности функции f(a, b, c) (табл. 3.1). Таблица 3.1. Таблица истинности функции f(a, b, c)
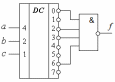
1 способ. f (a, b, c) = ( 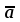 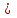 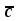 )( )(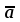 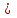 b)(b b)(b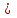 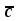 ) = &(1, 4, 5, 7) = y1 ) = &(1, 4, 5, 7) = y1 y4 y4 y5 y5 y7. y7.Для получения схемы достаточно определить выходы дешифратора (с активным нулем на выходах), соответствующие входящим в функцию конституентам нуля и соединить их с входами конъюнктора. Если на входы дешифратора будут поданы входные переменные, то на выходе конъюнктора сформируется значение функции (рис. 3.1,а). 2 способ. Найдем отрицание СКНФ функции Y (a, b, c): 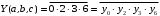 . . Для получения схемы достаточно выходы дешифратора соединить с помощью элемента И-НЕ (рис. 3.1.б).
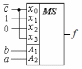
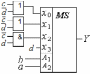
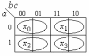
Рис. 3.1. Реализация логической функции f(a, b, c) = ( 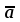 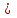 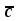 )( )(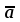 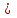 b)(b b)(b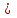 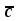 ) )на основе дешифратора Задание №4.Тема: Синтез комбинационных схем на основе мультиплексоров 1. Реализовать функцию трех переменных (см. задание 3) с помощью мультиплексора а) типа «8-1»; б) типа «4-1». Решение. a) Реализуем заданную логическую функцию трех переменных на мультиплексоре типа «8-1». Функция задана в СКНФ. По таблице 3.1 определили, что f (a, b, c)= &(1, 4, 5, 7). На адресные входы подадим входные переменные, а информационные входы, соответствующие входящим в функцию конституентам нуля, соединим с шинами земли (0), остальные информационные входы соединяются с шинами питания (1). На выходе мультиплексора формируется значение функции (рис. 4.1). 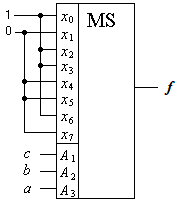 Рис. 4.1. Реализация функции f (a, b, c) на мультиплексоре типа «8-1» б) Для реализации функции f (a, b, c) = ( 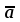 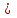 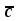 )( )(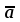 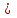 b)(b b)(b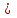 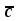 ) с помощью мультиплексора типа «4-1» используем карту Карно. Сначала выберем одно из сочетаний двух переменных ab, ac, bc, которые являются управляющими и подаются на адресные входы мультиплексора. На информационные входы в этом случае могут быть поданы четыре функции одной (третьей) переменной. ) с помощью мультиплексора типа «4-1» используем карту Карно. Сначала выберем одно из сочетаний двух переменных ab, ac, bc, которые являются управляющими и подаются на адресные входы мультиплексора. На информационные входы в этом случае могут быть поданы четыре функции одной (третьей) переменной. На рис.4.2а-б-в показано соответствие информационных входов мультиплексора x0, x1, x2, x3 определенным адресным входам мультиплексора «4-1».
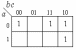
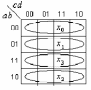
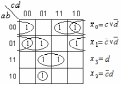
Рис. 4.2. Соответствие информационных входов мультиплексора «4-1» управляющим сигналам: а) a и b, б)а и с, в) b и с Таким образом, карта Карно на три переменные разбивается как бы на четыре двухклеточные карты на одну переменную. Затем минимизируется набор из четырех функций одной переменной и получаются необходимые значения сигналов на информационных входах мультиплексора для заданной функции (рис. 4.3 а-б-в-г).
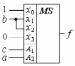
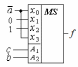
Рис. 4.3. Реализация функции f (a, b, c) на мультиплексоре типа «4-1» 2. Реализовать функцию четырех переменных (см. задание 2.1) с помощью мультиплексора а) типа «16-1»; в) типа «4-1». Решение. a) Функция Y= 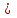 (0,2,3,4,5,6,9,13,15) задана номерами наборов переменных, на которых принимает значение единицы. Подадим на входы мультиплексора с указанными номерами значение 1, на остальные 0 (рис.4.4). (0,2,3,4,5,6,9,13,15) задана номерами наборов переменных, на которых принимает значение единицы. Подадим на входы мультиплексора с указанными номерами значение 1, на остальные 0 (рис.4.4).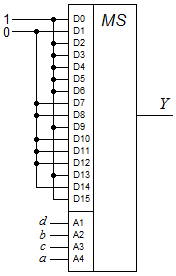 Рис. 4.4. Реализация функции Y(a, b, c, d) на мультиплексоре типа «16-1» в) Реализуем заданную логическую функцию четырех переменных Y(a,b,c,d) на мультиплексоре типа «4-1». Выберем в качестве управляющих сигналов переменные a и b. Покажем на карте Карно для функции четырех переменных (a,b,c,d) расположение информационных сигналов (x0,x1,x2,x3) мультиплексора «4-1» (рис. 4.5а). Отобразим на карте Карно заданную функцию (рис. 4.5б) и проведем для каждого xi минимизацию. Для реализации заданной функции на информационные входы мультиплексора «4-1» необходимо подать соответствующие значения переменных c и d (рис. 4.5в).
Рис. 4.5. Реализация функции Y (a, b, c, d) на мультиплексоре типа «4-1» |

 а)
а)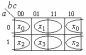 б)
б)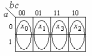 в)
в)