фм. Практическая работа по Финансовая математика

• Название: Практическая работа по Финансовая математика
• Дата: 11.05.2019
• Размер: 57.27 Kb.
• Имя файла: фм.docx
• Тип: Практическая работа; #76699

Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическая работа

по	«Финансовая математика»

дисциплине

Выполнил(а) студент(ка)	Лила Елена Алексеевна
			фамилия имя отчество
Идентификационный номер:		801-0701-6

Пермь 2019год

ВАРИАНТ 4
Задача 1
Банк выдал кредит на 6 месяцев в размере 150 тыс. руб. При ожидаемом месячном уровне инфляции в 1,5% реальная доходность операции равна 24% годовых. Определите ставку процентов по кредиту с учетом инфляции, погашаемую сумму и сумму начисленных процентов.
Решение:
Определим годовой уровень инфляции.

Инфляция является цепным процессом, следовательно, индекс цен за несколько периодов равен произведению цепных индексов цен.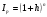

,

где I_р - индекс цен

h – постоянный темп инфляции

n – число периодов.
I_р = (1 + 0,024)¹² = 1, 3292

h_год = 1,3292 – 1 = 0,3292 = 32,92%.
Брутто–ставка процента – это ставка процента, индексированная с учетом роста уровня цен для учета инфляции (ставка при которой капитал действительно растет с необходимой доходностью).

Определяется по формуле Фишера:

r = + h + * h

где r – номинальная процентная ставка

- безинфляционная ставка, отражающая реальную доходность операции

h – уровень инфляции.
r = 0,24 + 0,3449 + 0,24 * 0,3449 = 0,6677 = 66,77%
Формула наращения по сложным процентам:

S = P * (1 + i)ⁿ ,

где S - наращенная сумма,

Р – начальная сумма,

n - число лет,

i - процентная ставка, выраженная десятичной дробью
S = 150000 * (1 + 0,6677)^0,5 = 193709,19 руб.
Величина полученного процента определяется по формуле:

I = S - P

где I – сумма процентов,

S – наращенная сумма,

P – первоначальная сумма
I = 193709,19 – 150000 = 43709,19 руб.

Ответ: ставка процентов по кредиту с учетом инфляции равна 66,77%, погашаемая сумма равна 193709,19 руб., сумма начисленных процентов равна 43709,19 руб.

Задача 2
При учете векселя на сумму 250 тыс. руб., до срока оплаты которого осталось 90 дней, банк выплатил его предъявителю 225 тыс. руб. Определите учетную ставку, которую использовал банк, если расчетное число дней в году равно 360.

Решение:

Определим учетную ставку, которую использовал банк по следующей формул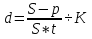е:

, где
d – учетная ставка в относительных единицах;

S – сумма по векселю;

t – количество дней от даты учета до даты погашения векселя;

Р – сумма полученная предъявителем векселя;

К - число дней в году.

Подставим значения в формулу:

d = = 0,3999 (39,99%)

Ответ: Учетная ставка, которую использовал банк =39,99%
Задача 3
Вклад в сумме 3000 руб. размещен в банке на полгода с ежемесячным начислением сложных процентов по ставке 8% годовых. Определите доход вкладчика по окончании срока договора.
Решение:

Определим доход вкладчика по окончании срока договора следующим образом:

Количество периодов начисления равно:

1*6=6

Следовательно, накопленная сумма составит:

S=3000 (1+)⁶ = 3184,6

Доход вкладчика по окончании срока договора будет равен:

I=3184,6 -3000 = 184,6 руб.

Ответ: Доход вкладчика по окончании срока договора =184,6 руб.
Задача 4
Депозитный сертификат номиналом 10000 руб. был куплен за девять месяцев до срока его погашения по учетной ставке 30% годовых и продан за три месяца до срока его погашения по ставке 15% годовых. Определите доход от операции купли-продажи и ее доходность в виде эффективной ставки простых процентов.

Решение:
Если вексель или другой вид долгового обязательства через некоторое время после его покупки и до наступления срока погашения продан, то эффективность этой операции можно измерить в виде простых или сложных процентов. Финансовая результативность операции здесь связана с разностью цен купли-продажи, которые в свою очередь определяются сроками этих актов до погашения векселя и уровнем учетных ставок. 

Цена в момент покупки составила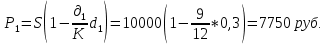



За 3 месяца до погашения сертификат был продан с дисконтированием по ставке 15%: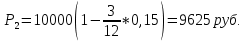



Инвестиции в начале операции составили, таким образом, 7750 руб., отдача от них 9625 руб. Операция продолжалась 6 месяцев. Наращение вложений за указанный срок по простой или сложной годовой ставке, которую принимают в качестве меры эффективности, должно дать конечный результат, т.е. 9625.

Доходность купли-продажи сертификата (в виде ставки простых процентов)


Задача 5


Банк установил следующий курс доллара США к рублю: • покупка -61,116; • продажа63,436. Определите: а) сколько долларов США клиент банка может купить за 5000 руб. (с учетом 1% налога на покупку наличной иностранной валюты)? б) сколько рублей клиент банка может получить за 500 долларов США?
Решение:

1. 
   Определим, сколько долларов США клиент банка может купить за 5000 руб. (с учетом 1% налога на покупку наличной иностранной валюты):
   

D = R / К_пр * (1 – Н / 100%),

где R – сумма денег в рублях;

К_пр – курс продажи доллара США к рублю;

Н – ставка налога на покупку наличной иностранной валюты.

D = 5000 / 63,436 * 0,99 = 78 долл.

2. 
   Рассчитаем, сколько рублей клиент может получить за 500 долларов США:
   

R = D * К_пок,

где К_пок – курс покупки доллара США к рублю.

R = 500 * 61,116 = 30558 руб.