Задачи финмат. Решение. В нашем случае для годовой ставки i простых процентов наращенная сумма s s p ( 1 n i ), (1)

• Название: Решение. В нашем случае для годовой ставки i простых процентов наращенная сумма s s p ( 1 n i ), (1)
• Анкор: Задачи финмат
• Дата: 25.04.2022
• Размер: 1.22 Mb.
• Имя файла: finmat3.doc
• Тип: Решение; #494861

Решение задач по финансовой математике.

Задача 1.1.

Ссуда в размере 225 тыс. $ выдана 16.01 по 10.11 включительно, под 5,75% простых годовых, год високосный. Насколько больше будет наращенная сумма ссуды при использовании обыкновенных процентов по сравнению с наращенной суммой при использовании точных процентов, если продолжительность пользования ссудой вычисляется точно?

Решение.

В нашем случае для годовой ставки i простых процентов наращенная суммаS:

S = P(1 + n∙i), (1)

где 1 + n∙i — множитель наращения, а годовая ставка i простых процентов (rateofinterest). В нашем случае срок финансового соглашения n измеряется не в годах, а в днях t, то в (1) в качестве n следует взять , где K — так называемая временная база, т.е. число дней в году, K = 360, 365(366). Если временная база K = 360 дней (12 месяцев по 30 дней), то говорят, что в формуле (1) используют обыкновенные, или коммерческие проценты.

а) точные проценты с точным числом дней ссуды. Этот вариант
(K = 365(366)) дает самые точные результаты.

S = 225∙(1+0,0575∙(285-16)/366) = 234,509 тыс. $.

б) обыкновенные проценты с точным числом дней ссуды. Этот метод (K = 360), иногда называемый банковским, распространен в ссудных операциях коммерческих банков. Он дает несколько больший результат, чем предыдущий метод.

S = 225∙(1+0,0575∙(285-16)/360) = 234,667 тыс. $.

Определим разницу наращенной суммы в первом и во втором случаях:

234,667 – 234,509 = 158 $.

Наращенная сумма при использовании обыкновенных процентов больше на 158$, нежели чем при использовании точных процентов.

Задача 2.1.

На годовом рублевом депозите ставка процентов составляет 195% годовых. Месячный темп инфляции в первом полугодии был постоянен и составил 4,7% в месяц, во втором полугодии — 5% в месяц. Во сколько раз возрастет реальная наращенная сумма депозита за год?

Решение.

Так как инфляция является цепным процессом, т.е. цены в период t повышаются на h_t процентов относительно уровня, сложившегося в периоде t–1, то индекс цен заn таких периодов равен произведению цепных индексов цен:

.

Найдем индекс цен за год:

J_p = (1+4,7/100)⁶∙(1+5/100)⁶ = 1,7653.

Тогда реальная ставка наращения:

I_r = I / J_p = 2,95 / 1,7653 = 1,6711.

Реальная ставка наращения составляет 67,11% годовых.
Задача 3.1.

На протяжении 25 лет создается резервный фонд. На поступающие в него средства начисляются сложные проценты по ставке 9,75% годовых. В течение первых 10 лет в конце каждого года в фонд вносили по 10 тыс. $, в течение последующих 10 лет – по 20 тыс. $ в конце года, а в последние 5 лет – по 25 тыс. $ в конце года. Чему будет равна сумма фонда через 25 лет?

Решение.

Найдем сумму фонда через 25 лет. Для этого воспользуемся формулой: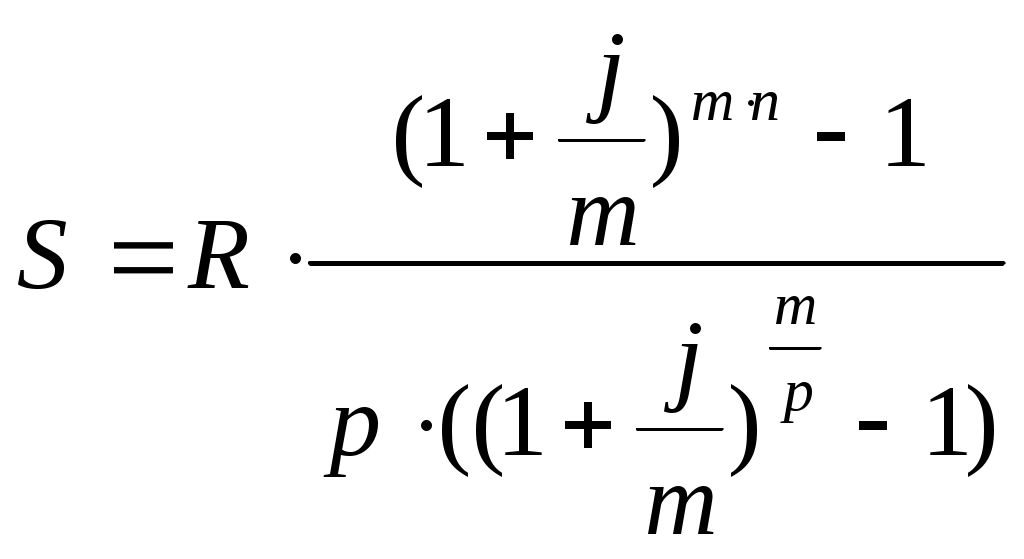

, где R – разовый рентный платеж , j – номинальная процентная ставка ренты , m и p число периодов начисления процентов и платежей в году , n – число лет. В нашем случае m=n=1.
Определим сумму фонда через 10 лет:



S₁₀ = 157,476 тыс.$.

Определим сумму через 20 лет: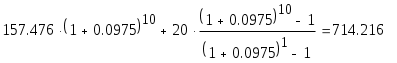



S₂₀ = 714,216 тыс.$.

Определим сумму через 25 лет:



Сумма фонда через 25 лет составит 1289 тыс.$.
Задача 4.1.

Какую сумму разовым платежом нужно положить в банк под 8 годовых мужчине в возрасте 40 лет, чтобы по достижении им пенсионного возраста в 60 лет в течение 20 лет в начале каждого месяца снимать по 200$, если проценты капитализируются: а) в конце года; б) в конце каждого полугодия?

Решение.

А) проценты капитализируются в конце года.

Определим сумму вклада мужчины когда ему исполнится 60 лет по формуле:

,

где р – число выплат (р=12), m – число раз присоединения процентов в году.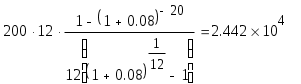



Следовательно в течении 20 лет мужчина должен накопить 24420$.

Тогда сумма на счету в возрасте 40 лет определяется из соотношения:




В возрасте 40 лет мужчина должен положить в банк 5239$.

Б) проценты капитализируются в конце полугодия.

Определим сумму вклада мужчины когда ему исполнится 60 лет по формуле:

,

где р – число выплат (р=12), m – число раз присоединения процентов в году.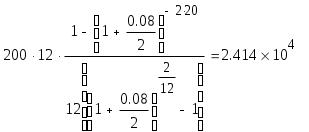



Следовательно в течении 20 лет мужчина должен накопить 24140$.

Тогда сумма на счету в возрасте 40 лет определяется из соотношения: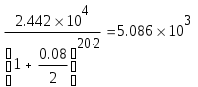




В возрасте 40 лет мужчина должен положить в банк 5086$.
Задача 5.1.

Кредит в сумме 280 тыс. $ выдан на 7 лет под 9,2% годовых и предусматривает погашение основного долга равными суммами, выплачиваемыми вместе с процентами в конце каждого полугодия. Намеченные к погашению восьмой и девятый платежи не были сделаны по каким-то причинам. В дальнейшем график выплат был восстановлен, но при этом пришлось увеличить равные выплаты, идущие в счет погашения основного долга. На сколько пришлось увеличить разовые выплаты по погашению основного долга?

Решение.

Определим величину годового запланированного платежа: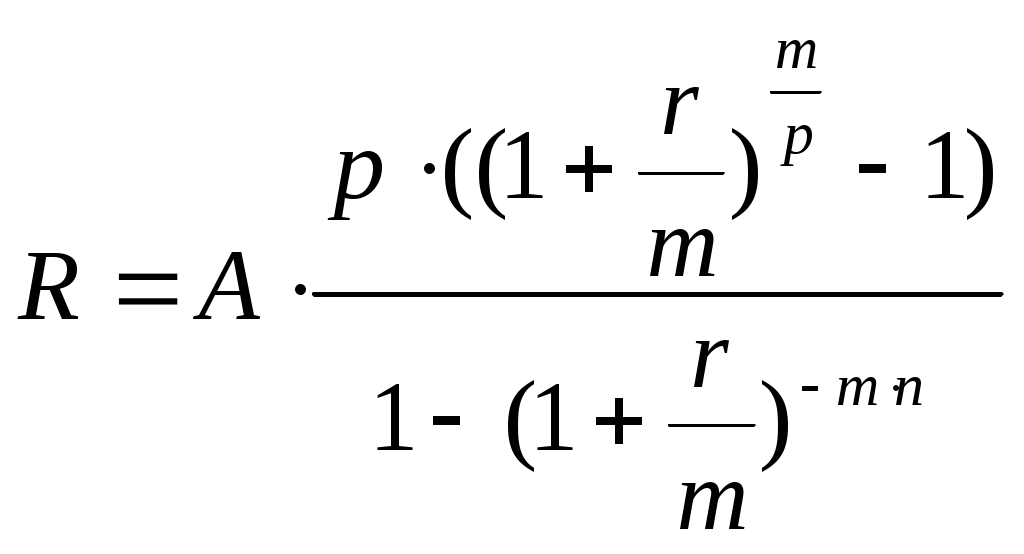

,

где р – число выплат (р=2), m – число раз присоединения процентов в году (m=2).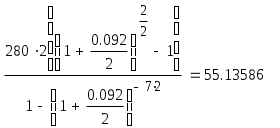



В год клиент должен был выплачивать 55135,86$ ежегодно.

В первую выплату в счет погашения суммы долга уйдет сумма:



Найдем суммы которые пойдут на погашения в остальных платежах.



Проверка:



Сумма погашения долга после 7-го платежа:



Тогда остаток долга:



Размер нового платежа определим по формуле:

,

Где t – количество лет, на которое отложена была рента.

Находим:



Увеличение разовых выплат по погашению долга составит:



Разовые выплаты по погашению долга увеличатся на 12884$.

Вариант 3.
Задание 1.

Банк принимает вклады на срочный депозит на следующих условиях : процентная ставка при сроке 35 дней – 45% ; при сроке 65 дней – 48% ; при сроке 90 дней – 50% . Рассчитайте доход клиента на указанные сроки . Год не високосный . Методика расчета: точные проценты с точным числом дней .

Решение.

Определим наращенную сумму вклада по формуле :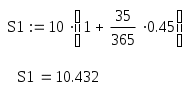

, где t – число дней ссуды ; К - продолжительность года в днях .



Наращенная сумма вклада составляет 10,432 млн. р.

Определим доход клиента :



Доход клиента составляет 0,432 млн. р.



Наращенная сумма вклада составляет 10,855 млн. р.

Определим доход клиента :



Доход клиента составляет 0,855 млн. р.



Наращенная сумма вклада составляет 11,233 млн. р.

Определим доход клиента :



Доход клиента составляет 1,233 млн. р.

Предприятие получило кредит на 3 года под годовую процентную ставку 40%.
Комиссионные составляют 5% от суммы кредита. Определите эффективную процентную ставку кредита, если: кредит получен под сложные проценты с начисление процентов : а) один раз в год , б) поквартально , в) ежемесячно .

Решение .

Для решения задачи воспользуемся формулой :

, где j-номинальная годовая ставка , m-число раз начисления процентов в году, n-число полных лет. Р – первоначальная сумма кредита , S – наращенная сумма кредита .

Определим эффективную процентную ставку кредита :

а)

Эффективная процентная ставка составляет 179,4%

б)



Эффективная процентная ставка составляет 218,8%

в)



Эффективная процентная ставка составляет 230,6%

Задание 3.

Четыре векселя номинальной стоимостью 50 млн. р. , 50 , 35 , 62 млн. р. со сроками погашения 25 , 62 , 50 , 110 дней требуется объединить в один со сроком погашения 95 дней . Объединение происходит : а) по ставке простых процентов – 60% , б) по ставке сложных процентов – 60% годовых . Определить стоимость объединенного векселя . Число дней в году принять за 360 .

Решение.

Если объединяются несколько платежей , то сумма нового платежа , исходя из простой процентной ставки , определяется по формуле :

,

где S₀ – сумма консолидированного платежа ; S_j – сумма платежей , у которых n₀n_j ; S_k – сумма платежей , у которых n₀<n_k ; n₀ – срок консолидированного платежа ; n_j , n_k – сроки отдельных платежей ; t_j , t_k – интервалы времени между сроками платежей и сроком консолидированного платежа ; i – процентная ставка .

а) по ставке простых процентов – 60% годовых .



Стоимость объединенного векселя по ставке простых процентов составляет 206,7 млн. р.

б) по ставке сложных процентов – 60% годовых .


Стоимость объединенного векселя по ставке сложных процентов составляет 207 млн. р.

Задание 4.

Инвестору с капиталом 600 млн. р. предлагают следующие независимые проекты :

Таблица 1 .

№проекта	Инвестиции, млн.р	Годовые поступления , млн.р.
		1	2	3	4	5	6
1	300	280	120	100
2	400	200	200	200	200
3	200	100	100	100	100	100
4	600	300	200	200	200	100	50

Цена денег – 18 % годовых . Какую оптимальную комбинацию выбрать , если проекты делимы ?

Решение .

Для каждого проекта определяем приведенную стоимость поступлений от инвестиций по формуле : , где S_i – поступления в i-ый период времени , r- рыночная процентная ставка .

Определяем чистую приведенную стоимость : , где Е- затраты на проект .

Рентабельность проекта R=NPV/E

Для удобства математических вычислений используем пакет Mathcad .

Для 1-го проекта :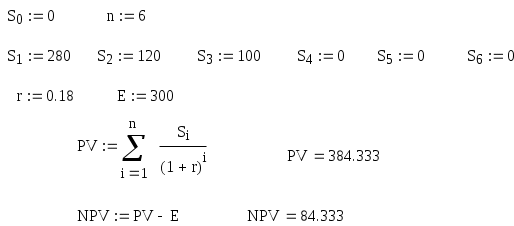



R=84.333/300=0.281 или 28,1%

Для 2-го проекта :



R=138.012/400=0.345 или 34,5%

Для 3-го проекта :



R=112.717/200=0.564 или 56,4%

Для 4-го проекта :



R=84.991/600=0.142 или 14,2%
Анализируя полученные данные можем сказать , что наиболее выгодными будут вложения в 2-ой и 3-ий объекты . Для данных объектов рентабельность наибольшая и составляет 34,5% и 56,4% соответственно .

Задание 5.

Организация приобрела 20 облигаций со сроком погашения 3 года и номинальной стоимостью 250 млн. р. по курсу 90 . Проценты начисляются по полугодиям по номинальной процентной ставке 54% годовых . Определить доход полученный организацией и эффективную процентную ставку доходности , если процентные деньги реинвестируются под 48% годовых с ежемесячным начислением процентов . Какая реальная ставка доходности , если уровень инфляции в первый год составил 26% , второй – 16%, третий – 12 % ?

Решение .

Определим доход , полученный организацией двумя способами .

Первый способ ( с помощью ренты ).

Проценты , выплачиваемые за полугодие : R = 20 · 250 · 0,54 / 2 = 1350 млн. р.

Найдем доход , полученный при размещении средств на счету . Для этого воспользуемся формулой :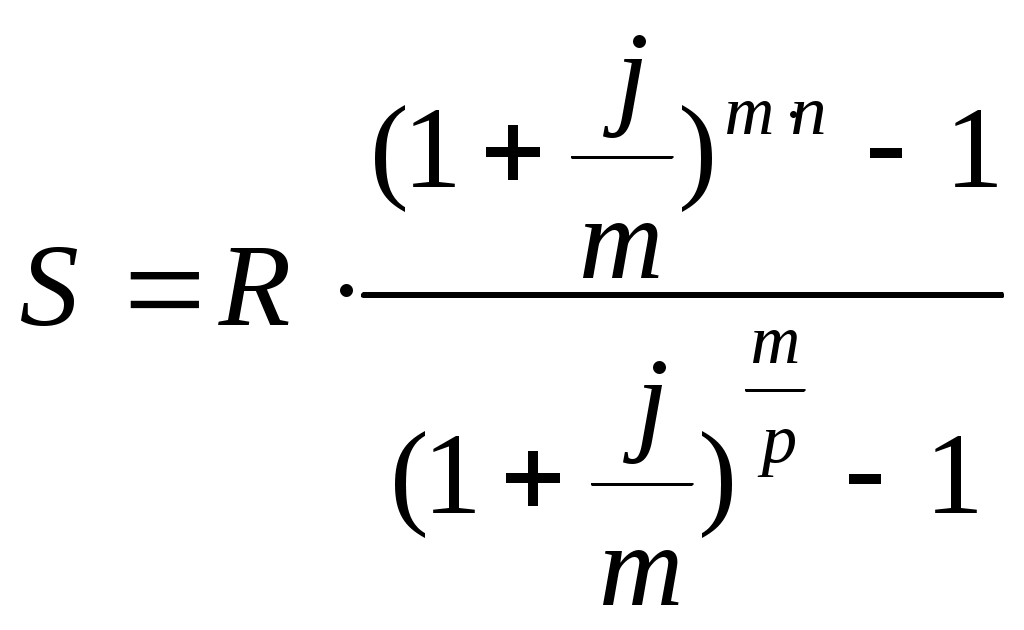

, где R – разовый рентный платеж , j – номинальная процентная ставка ренты , m и p число периодов начисления процентов и платежей в году , n – число лет .

Находим :



Доход организации составляет 15790 млн. р.

Второй способ .

Определим доход инвестора к концу первого года :



Доход к концу первого года составляет 3058 млн. руб.

Определим доход инвестора к концу второго года :



Доход к концу второго года составляет 7926 млн. руб.

Определим доход инвестора к концу третьего года :



Доход к концу третьего года составляет 15790 млн. руб.

Определим эффективную ставку доходности из соотношения :

S₁ = 15790 + 20 · 250 = 20790 млн.р. ; Р = 20 · 250 · 0,96 = 4800 млн.р.

, доходность операции составляет 63% годовых .

Определим реальную ставку доходности .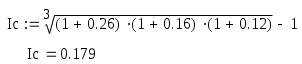

, где



Находим :



Реальная ставка доходности 38,3 % годовых .

Задача 6.

Стоимость товара 1200 млн. р. Покупатель выписал 5 векселей с последовательным погашением через месяц . Проценты , включенные в вексель начисляются на остаток задолженности по ставке 51% годовых . Продавец учел векселя по годовой учетной ставке 48% . Определить стоимость каждого векселя и сумму , полученную продавцом . Какой должен быть корректирующий множитель и какая скорректированная стоимость каждого векселя , чтобы продавец получил полную стоимость ? Определить текущую задолженность покупателя , если он выдал скорректированные векселя , а рыночная процентная ставка 60% .
Решение.

Для удобства математических вычислений воспользуемся пакетом Mathcad .

Число векселей :



Проценты , включенные в вексель начисляются на остаток задолженности :



Учетная ставка векселей :



Стоимость товара (млн. р. ):



Рыночная процентная ставка :



Сумма векселя погашаемого в t-ый момент времени , рассчитывается по формуле :





Векселя имеют стоимость :

V₁=291 млн.р.

V₂=280,8 млн.р.

V₃=270,6 млн.р.

V₄=260,4 млн.р.

V₅=250,2 млн.р.

Сумма полученная продавцом (млн. р.) :





Сумма полученная продавцом составляет 1195 млн. р.

Корректирующий множитель :



Стоимость товара (млн. р.):



Следовательно стоимость товара должна быть 1205 млн. р.

Определим скорректированную сумму каждого векселя (млн.р.) :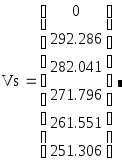





Скорректированные стоимости векселей :

Vs₁=292 млн.р.

Vs₂=282 млн.р.

Vs₃=272 млн.р.

Vs₄=262 млн.р.

Vs₅=251 млн.р.

Определим текущую задолженность покупателя. Рыночная ставка за месяц :



Текущая задолженность покупателя (млн. р.) :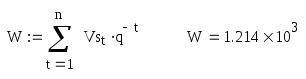



Таким образом текущая задолженность покупателя составит 1214 млн. р.


Задача 1.4.

На сумму в 2255$ в течение 9 месяцев начисляются простые проценты. Базовая ставка 5% годовых повышается каждый месяц, начиная со второго, на 0,5%, временная база K= 360. Чему будут равны наращенная сумма и средняя процентная ставка?

Решение.

Так как начисление идет по ставке простых процентов, т. е. без капитализации вклада (начисление процентов происходит на первоначальную сумму вклада, без присоединения капитализированной суммы ежемесячно), то наращенную сумму вклада определим по формуле:

= 2255∙(1 + 0,05/12+ 0,055/12+ 0,06/12+ 0,065/12+ +0,07/12+ 0,075/12 + 0,08/12 + 0,085/12+ 0,9/12) = 2373,3875$.

Средняя процентная ставка составляет: (5 + 5,5 + 6 + 6,5 + 7 + 7,5 + 8 + 8,5 + 9)/9 = 7%.

Средняя процентная ставка за 9 месяцев составляет 7% годовых.

Задача 2.4.

По условиям предыдущей задачи консолидация платежей производится на основе банковской учетной ставки 9,25% годовых, K= 365 дней. Какова величина S?

Решение.

Определим величину платежа. Так как консолидация платежей происходит на основе банковской простой учетной ставки, то используем для вычисления формулу простых процентов:

S = P∙(1 - d∙(n/365))

S = 20,5∙(1 – 0,0925∙(2/365)) + 32∙(1 – 0,0925∙(38/365)) + 9,4∙(1 – 0,0925∙(108/365)) + 8,25∙(1 – 0,0925∙(196/365)) = 20,49 + 31,692 + 9,143 + 7,84 = 69,435 тыс. $.

Задача 3.4.

В течение 12 лет создается фонд, на поступающие в конце года средства начисляется 9% годовых. Годовой взнос – 10 тыс. $. В первые 6 лет взносы поступали в конце года, в следующие 4 года – по полугодиям и в последние 2 года – в конце каждого квартала. Определите величину фонда.

Решение.

Найдем сумму фонда через 12 лет. Для этого воспользуемся формулой: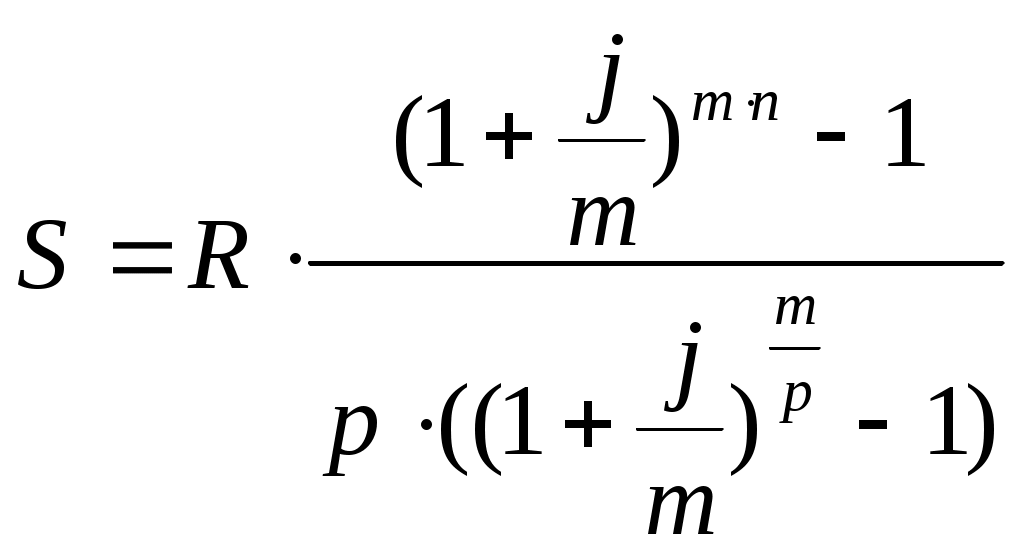

, где R – годовой рентный платеж , j – номинальная процентная ставка ренты , m и p число периодов начисления процентов и платежей в году , n – число лет. В первом случае m=n=1.
Определим сумму фонда через 6 лет:



S₁₀ = 75,233 тыс.$.

Определим сумму через 10 лет: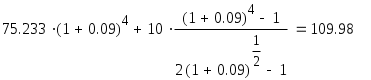



S₂₀ = 109,98 тыс.$.

Определим сумму через 12 лет:



Сумма фонда через 12 лет составит 131,277 тыс.$.

Задача 4.4.

В течение 9 лет создается фонд. Денежные поступления в фонд – в начале года равными суммами. На собранные средства в конце года начисляется 22% годовых. Насколько процентов возрастет наращенная сумма фонда при переходе к поквартальным взносам в начале каждого квартала и поквартальному начислению процентов в конце каждого квартала?

Решение.

Определим коэффициент наращения для каждого способа начисления процентов по формуле:

,

где j – номинальная процентная ставка ренты , m и p число периодов начисления процентов и платежей в году, n – число лет.

В первом случае: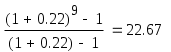



Во втором случае: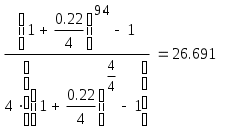



Определим во сколько раз, возрастет величина фонда во втором случае по сравнению с первым случаем:



Наращенная сумма фонда будет во втором случае больше наращенной суммы в первом случае на 17,7%.
Задача 5.4.

Решено погасить долг равными срочными платежами постнумерандо в конце каждого года (см. условия предыдущей задачи). После 3 лет погашения задолженности, согласно намеченному графику, было решено в течение последующих трех лет гасить основную задолженность равными полугодовыми платежами. Чему будут равны суммарные расходы должника по обслуживанию долга?

Решение.

Определим величину годового запланированного платежа: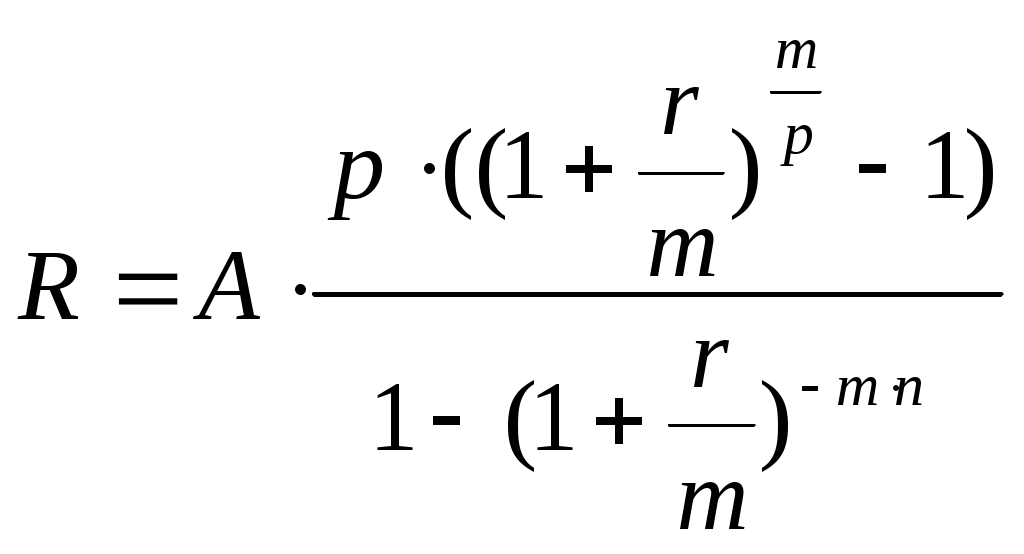

,

где р – число выплат (р=1), m – число раз присоединения процентов в году (m=1).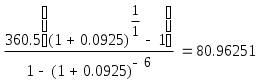



В год клиент должен был выплачивать 80.96251$.

В первую выплату в счет погашения суммы долга уйдет сумма:



Найдем суммы, которые пойдут на погашения в остальных платежах.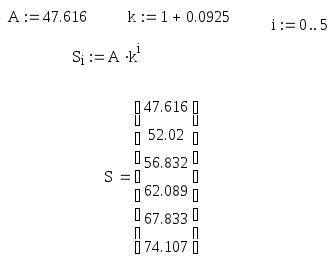



Проверка:



Сумма погашения долга после 3-го платежа:



Тогда остаток долга:



Размер нового платежа определим по формуле: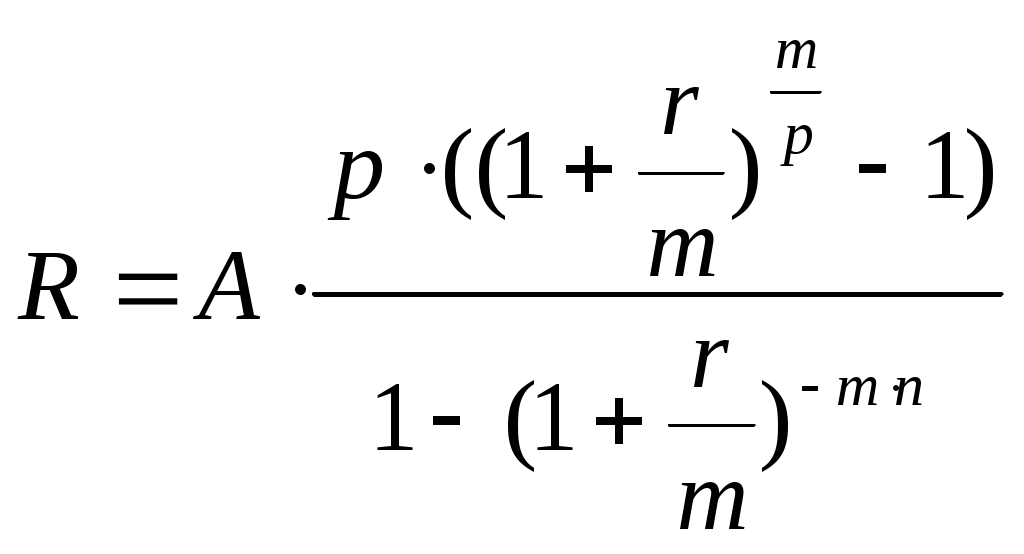

,

Находим:



Тогда суммарные расходы должника:



Суммарные расходы должника составят 480,404$.

Помощь на экзамене онлайн.