задачи. 334032 финансовая математика. Задача 6. 7 Какова эффективная ставка процентов, если номинальная ставка равна 21% при помесячном начислении процентов

• Название: Задача 6. 7 Какова эффективная ставка процентов, если номинальная ставка равна 21% при помесячном начислении процентов
• Анкор: задачи
• Дата: 27.03.2023
• Размер: 33.53 Kb.
• Имя файла: 334032 финансовая математика.docx
• Тип: Задача; #1018427

Задача №6.7


Какова эффективная ставка процентов, если номинальная став­ка равна 21% при помесячном начислении процентов?
Дано : j=0,21, m=12

Найти : i_эфф
Решение
Эффективная ставка отвечает на вопрос : какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как и при m-разовом начислении процентов в году по ставке j/m.

Формула эквивалентности для эффективной ставки:

i_эфф = -1,

где i – эффективная ставка

j – номинальная ставка;

m – периодичность начисления процента.
i_эф = (1 + )¹² – 1 = 0,2314 или 23,14%.
Ответ : эффективная ставка процентов равна 23,14%.
Задача №7.7

Финансовый документ на сумму 10 000 000 р., срок платежа по которому наступает через 5 лет. Определить:

1) сумму, полученную при поквартальном дисконтировании по номинальной сложной учетной ставке 20% в год.

2) эффективную учетную ставку.
Дано : S = 10 000 000, n=5, m=4, f = 0,20

Найти : P, d_эф
Решение
При дисконтировании m раз в году используется номинальная учетная ставка. Расчет дисконтированной величины производится по формуле :

P = S * (1 - 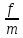)^m*n

где Р – приведенная (дисконтированная) сумма,

S – наращенная сумма

n – число лет.

m – число начислений в год

f – номинальная учетная ставка

P = 10 000 000 * (1 – 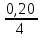)^4*5 = 3 584 859,22 р.
При дисконтировании m раз в год возникает понятие эффективной учетной ставки, под которой понимают сложную годовую учетную ставку, эквивалентную номинальной учетной ставке при заданном значении m. Она определяется по формуле :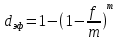

,

где f - номинальная сложная учетная ставка,

m – число начислений в год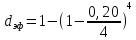
= 0,1855 или 18,55%.
Ответ : 1) полученная сумма равна 3 584 859,22 р., 2) эффективная учетная ставка равна 18,55%.


Задача № 8.4

Найти величину ежегодных налоговых платежей при условии, что сумма депозита составляет 5000 руб., сложная ставка наращения равна 15%, срок депозита - 4 года, налоговая ставка на проценты - 10%.
Дано : P = 5 000, i= 0,15, n=4, g=0,10

Найти : G
Решение
По этому варианту сумма налога определяется за каждый истекший год. Эта величина переменная – с ростом наращенной суммы растет и сумма налога. Расчет налога на проценты за t-й год определяется как :

G_t = Р*(1+i)^t-1 * i * g,

где P – вложенная сумма,

i – сложная процентная ставка,

g - ставка налога на проценты,

t – t-й год
G_1год = 5 000*(1+0,15)^1-1 * 0,15 * 0,10 = 75,00 руб.

G_2год = 5 000*(1+0,15)^2-1 * 0,15 * 0,10 = 86,25 руб.

G_3год = 5 000*(1+0,15)^3-1 * 0,15 * 0,10 = 99,19 руб.

G_4год = 5 000*(1+0,15)^4-1 * 0,15 * 0,10 = 114,07 руб.
Ответ : величина ежегодных налоговых платежей равна 1год – 75,00 руб., 2год - 86,25 руб., 3год - 99,19 руб., 4год - 114,07 руб.
Задача № 9.5

Последовательный прирост цен по месяцам составляет:

b1 = 20%,

b2 = 27%,

b3=30%.

Определить:

1) индекс цен за 3 месяца;

2) темпы инфляции за 3 месяца.
Дано : b1 = 0,20, b2 = 0,27, b3 = 0,30

Найти : Ip, h
Решение
При переменных уровнях инфляции за последовательные периоды, общий индекс инфляции определяется по принципу сложных процентов с изменяющимися процентными ставками:

Ip = Ip₁ * Ip₂ * ... * Ip_n,

где Ip – индексы инфляции в соответствующие периоды

или для нашего случая :

Ip = (1 + b₁) * (1 + b₂) * (1 + b₃)

где b – приросты цен в соответствующие периоды.
Ip = (1 + 0,20) * (1 + 0,27) * (1 + 0,30) = 1,9812.
Темп инфляции (inflation rate) показывает, на сколько процентов выросли цены за рассматриваемый период. Темп инфляции определяется как относительный прирост цен за период.

h = I_p - 1
h = 1,9812 – 1 = 0,9812 или 98,12%.
Ответ : 1) индекс цен за 3 месяца равен 1,9812; 2) темпы инфляции за 3 месяца равны 98,12%.
Задача № 10.1

Предполагается поместить 3000 долларов США на рублевый депозит. Курс продажи на начало срока депозита 27 рублей за 1 дол­лар США. Ожидаемый курс покупки 30 руб. Ставка наращения для депозита в рублях составляет 25%. Ставка наращения для конкрет­ного вида СКВ составляет 20%. Депозит размещен сроком на 6 меся­цев. Определить:

1. Конечную наращенную сумму в валюте.

2. Оценить прямое наращение по долларовой процентной ставке.
Дано : P = 3 000, k₀ = 27, k₁ = 30, i_руб = 0,25, i_валют = 0,20, n = 0,5

Найти : S
Решение
Так как срок 6 месяцев, то используем простые проценты.
1) При использовании только валютного депозита

без конверсии: Р’(СКВ) F’(СКВ)
Наращенная сумма определяется по формуле :

S = P * (1 + n*i) ,

где S – наращенная сумма;

P – первоначальная сумма;

i – ставка процентов;

n – число лет.
S = 3 000 * (1 + 0,5*0,20) = 3 300,00 долларов США.
2) При конвертации валюты и рублевого депозита

с конверсией: Р’(СКВ) Р (Руб.) F (Руб.) F’(СКВ)
Трём этапам операции (конверсия, наращение процентов, конверсия) соответствуют три сомножителя следующей формулы:

S_v = P_v * K₀ * (1+n*i) * ,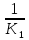

где Sv - наращенная сумма в валюте;

Pv - исходная сумма в валюте;

K0 и K1 — курсы валюты на начало и конец операции.
S = 3 000 * 27 * (1 + 0,5*0,25) * 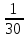= 3 037,50 долларов США.
Ответ : 1. конечная наращенная сумма в валюте равна при прямом наращении 3 300,00 долларов США, при конверсии - 3 037,50 долларов США, 2. прямое наращение по долларовой процентной ставке выгоднее.