Главная страница
Навигация по странице:

  • Практическая работа по предмету «Теория и практика развития предприятия»

  • З адача 3.13.

  • Решение: 1) Критерий максимакса

  • 2) Максиминный критерий Вальда

  • 3) Критерий минимаксного риска Сэвиджа

  • 4) Критерий пессимизма-оптимизма Гурвица

    		•

    Практичекая работа_задачи. Практическая работа по предмету Теория и практика развития предприятия


    Скачать 96.55 Kb.
    НазваниеПрактическая работа по предмету Теория и практика развития предприятия
    Дата16.12.2020
    Размер96.55 Kb.
    Формат файлаdocx
    Имя файлаПрактичекая работа_задачи.docx
    ТипПрактическая работа
    #161346

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

    Федеральное государственное бюджетное образовательное учреждение

    высшего образования

    «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ

    УНИВЕРСИТЕТ»

    Кафедра экономики предпринимательства

    Практическая работа

    по предмету «Теория и практика развития предприятия»

    Выполнил студент гр. Эк-230Мз Дегтярева М.А.
    Проверил д.э.н., профессор Бухарбаева Л.Я.

    Уфа 2020 г.

    З 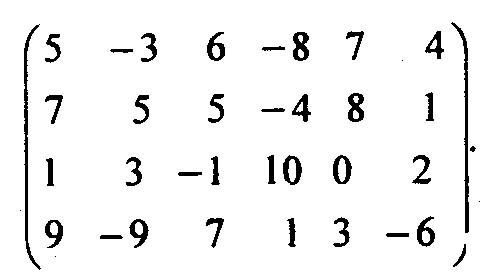адача 3.13. Найти наилучшие стратегии по критериям: максимакса, Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы - выигрыши):
    Решение:

    1) Критерий максимакса.

    С его помощью определяется страте­гия, максимизирующая максимальные выигрыши для каждого состояния природы. Это критерий крайнего оптимизма. Наилуч­шим признается решение, при котором достигается максималь­ный выигрыш, равный






    П1
    П2
    П3
    П4
    П5
    П6

    А1
    5
    -3
    6
    -8
    7
    4

    А2
    7
    5
    5
    -4
    8
    1

    А3
    1
    3
    -1
    10
    0
    2

    А4
    9
    -9
    7
    1
    3
    -6


    Для матрицы А наилучшим решением будет А3, при котором достигается максимальный выигрыш 10.

    2) Максиминный критерий Вальда.

    С позиций данного крите­рия природа рассматривается как агрессивно настроенный и сознательно действующий противник типа тех, которые проти­водействуют в стратегических играх. Выбирается ре­шение, для которого достигается значение

    Для платежной матрицы А каждой строке определяем минимальный элемент Wi= minaij

    W1= min {5;-3;6;-8;7;4}= -8

    W2= min {7;5;5;-4;8;1}= -4

    W3= min {1;3;-1;10;0;2}= -1

    W4= min {9;-9;7;1;3;-6}= -9

    Из полученных значений выбираем максимальное: W= maxminaij= max {-8;-4;-1;-9)= -1, значит оптимальной по данному критерию является стратегия А3.

    В соответствии с критерием Вальда из всех самых неудач­ных результатов выбирается лучший (W = -1). Это перестрахо­вочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определя­ется отношением игрока к риску.

    3) Критерий минимаксного риска Сэвиджа.

    В ыбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличи­ем, что игрок руководствуется не матрицей выигрышей А , а матрицей рисков R ,

    Составляем матрицу рисков для каждой стратегии:
    r1
    r2
    r3
    r4
    r5
    r6

    А1
    9-5=4
    5-(-3)=2
    7-6=1
    10-(-8)=18
    8-7=1
    4-4=0

    А2
    9-7=2
    5-5=0
    7-5=2
    10-(-4)=14
    8-8=0
    4-1=3

    А3
    9-1=8
    5-3=2
    7-(-1)=8
    10-10=0
    8-0=8
    4-2=2

    А4
    9-9=0
    5-(-9)=14
    7-7=0
    10-1=9
    8-3=5
    4-(-6)=10



    Для матрицы рисков рассчитываем S:

    S 1 = 18

    S 2 = 14

    S 3= 8

    S 4 = 14

    Минимально возможный из самых крупных рисков, равный 8, достигается при использовании третьей стратегии А3.

    4) Критерий пессимизма-оптимизма Гурвица.

    Этот критерий при выборе решения рекомендует руководствоваться некоторым сред­ним результатом, характеризующим состояние между крайним пес­симизмом и безудержным оптимизмом. Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением



    p- коэффициент пессимизма, равен 0,2.

    H1= 0,2·(-8) + 0,8·7 =4

    H2= 0,2·(-4) + 0,8·8 =5,6

    H3= 0,2·(-1) + 0,8·10 =7,8

    H4= 0,2·(-9) + 0,8·9 =5,4

    Ha= max {4;5,6;7,8;5,4}= 7,8.

    Следовательно, оптимальная стратегия А3.

    Применительно к матрице рисков R критерий пессимизма-оптимизма Гурвица имеет вид:


    p - коэффициент пессимизма равен 0,4.

    H1= 0,4·18 + 0,6·0 =7,2

    H2= 0,4·14 + 0,6·0 =5,6

    H3= 0,4·8 + 0,6·0 =3,2

    H4= 0,4·14 + 0,6·0 =5,6

    HR= min {7,2;5,6;3,2;5,6}=3,2

    Следовательно, оптимальная стратегия по данному критерию - А3.

    Вывод: поскольку стратегия А3, фигурирует в качестве оптимальной по всем критериям выбора из четырех испытанных, степень ее надежности можно признать достаточно высокой для того, что­бы рекомендовать эту стратегию к практическому применению.
    Задача 3.15. При крупном автомобильном магазине планируется открыть мастерскую по предпродажному обслуживанию и гарантийно­му ремонту автомобилей. Консультационная фирма готова предоставить дополнительную информацию о том, будет ли рынок благоприятным или нет. Эти сведения обойдутся магазину в 13 тыс. руб. Администра­ция магазина считает, что эта информация гарантирует благоприятный рынок с вероятностью 0,5. Если рынок будет благоприятным, то боль­шая мастерская принесет прибыль в 60 тыс. руб., а маленькая - 30 тыс. руб. При неблагоприятном рынке магазин потеряет 65 тыс. руб., если будет открыта большая мастерская, и 30 тыс. руб.- если откроется маленькая. Не имея дополнительной информации, директор оценивает вероятность благоприятного рынка как 0,6. Положительный результат обследования гарантирует благоприятный рынок с вероятностью 0,8. При отрицательном результате рынок может оказаться благоприятным с вероятностью 0,3. Постройте дерево решений и определите:

    • Следует ли заказать консультационной фирме дополнительную информацию, уточняющую конъюнктуру рынка?

    • Какую мастерскую следует открыть при магазине: большую или маленькую?

    • Какова ожидаемая денежная оценка наилучшего решения?

    • Какова ожидаемая ценность дополнительной информации?

    Решение:
    Процедура решения заключается в построении дерева решения и вычисления для каждой вершины дерева ожидаемой денежной оценки с учетом вероятностей, и последующее отбрасывание неперспективных ветвей.


    Номер стратегии
    Действия компании
    Выигрыш, дол., при состоянии экономической среды

    благоприятном
    неблаго­приятном

    1
    Большая мастерская (а1)
    60000
    -65000

    2
    Маленькая мастерская (a2)
    30000
    -30 000





    Рис. 1 - Дерево решений
    Рассчитываем оценочную стоимость от принятого решения:

    0,6*60 000-0,4*65 000 =10 000

    0,6*30 000- 0,4*30 000 = 6 000

    0,8*60 000-0,2*65 000 = 35 000

    0,8*30 000-0,2*30 000 = 18 000

    0,3*60 000-0,7*65 000 = - 27 500

    0,3*30 000-0,7*30 000 = - 12 000

    0,5*35 000-0,5*12000= 11 500

    1. Анализируя дерево решений можно сделать вывод, что заказывать уточняющую информацию не следует, т.к. стратегия «не проводить исследование» показала лучший результат: 10 000, а стратегия «проводить исследования»: - 2500.

    2. Следует открыть большую мастерскую, т.к. ОДО наилучшего решения 10 000

    3. Если точная информация об истинном состоянии рынка будет благоприятной ОДО = 60 000, принимается решение открывать большую мастерскую; если неблагоприятной, то наиболее целесообразное решение – ничего не открывать ОДО=0

    ОДОт.и (ОДО точной информации) определяется выражением:

    ОДОт.и = 0,5 * 60 000 + 0,5 * 0 = 30000.

    4. Ожидаемая ценность точной информации равна:

    ОЦт.и = ОДОт.и - ОДО = 30 000 - 10 000 = 20 000.

    написать администратору сайта