таблицы истинности. Практическая работа «Построение таблиц истинности для логических. Практическая работа Построение таблиц истинности для логических выражений
 Скачать 60 Kb. Скачать 60 Kb.
|
|
Практическая работа «Построение таблиц истинности для логических выражений» 8 класс Цели: предметные - представление о таблице истинности для логического выражения; метапредметные - навыки формализации и анализа логической структуры высказываний; способность видеть инвариантную сущность внешне различных объектов; личностные - понимание роли фундаментальных знаний как основы современных информационных технологий. Решаемые учебные задачи: 1) проверка знания основных логических операций; 2) закрепление навыков формализации логических выражений; 3) рассмотрение алгоритма построения таблиц истинности; 4) отработка навыков построения таблиц истинности для логических выражений. Теоретические сведения. Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. Алгебра логики определяет правила записи, упрощения и преобразования высказываний и вычисления их значений. Конъюнкция – логическая операция, являющаяся истинным тогда и только тогда, когда оба исходных высказывания истинны. Дизъюнкция – логическая операция, являющаяся ложным тогда и только тогда, когда оба исходных высказывания ложны. Инверсия – логическая операция, которая в соответствие новое высказывание, значение которого противоположно исходному. Приоритет логических операций: инверсия, конъюнкция, дизъюнкция. Источники информации: Босова Л. Л. Информатика : учебник для 8 класса / Л.Л. Босова, А.Ю. Босова - Москва : БИНОМ. Лаборатория знаний , 2015 - 160 с. Босова Л. Л. Информатика : рабочая тетрадь для 8 класса в 2 частях. Ч.1 / Л.Л. Босова, А.Ю. Босова - Москва : БИНОМ. Лаборатория знаний, 2016 - 88 с. Босова Л. Л. Информатика : рабочая тетрадь для 8 класса в 2 частях. Ч.2 / Л.Л. Босова, А.Ю. Босова - Москва : БИНОМ. Лаборатория знаний, 2016 - 88 с. Ответы: а) 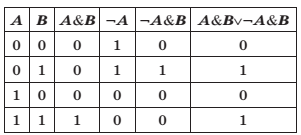 б) б) 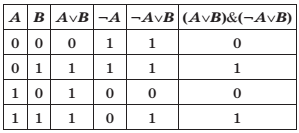
|
