ииииииииииииии. Практическая работа Решение задачи о назначениях
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
Практическая работа 6. Решение задачи о назначенияхЦель занятия: приобретение навыков построения математических моделей задач о назначении и решения этих задач в Microsoft Excel. Подготовка к работе: повторить методы решения транспортных задач, а так же порядок решения транспортных задач средствами табличного процессора. Порядок работы: Разобрать решение примера 1 с помощью алгоритма Венгерского метода. Найдите оптимальное решение примера 1 с помощью Excel. Найдите оптимальное решение примера 2 с помощью алгоритма Венгерского метода. Найдите оптимальное решение примера 2 с помощью Excel. Выполните задания на закрепление. Частным случаем транспортной задачи является задача о назначениях, в которой число пунктов производства равно числу пунктов назначения, т.е. транспортная таблица имеет форму квадрата. Задача о назначениях – это распределительная задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.д.), а каждый ресурс может быть использован на одной и только одной работе. То есть ресурсы не делимы между работами, а работы не делимы между ресурсами. Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно-исследовательским лабораториям и т.п. Любая задача о назначениях может быть решена с использованием методов линейного программирования или алгоритма решения транспортной задачи. Однако ввиду особой структуры данной задачи был разработан специальный алгоритм, получивший название Венгерского метода. Алгоритм решения задачи о назначениях Этот алгоритм состоит из трех этапов. Этап 1: 1. Формализация проблемы в виде транспортной таблицы по аналогии с решением транспортной задачи. 2. В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки. 3. Повторить ту же самую процедуру для столбцов. Теперь в каждой строке и в каждом столбце таблицы есть по крайней мере один нулевой элемент. Представленная в полученной с помощью описанного выше приема "приведенной" транспортной таблице задача о назначениях эквивалентна исходной задаче, и оптимальное решение для обеих задач будет одним и тем же. Сущность Венгерского метода заключается в продолжении процесса приведения матрицы до тех пор, пока все подлежащие распределению единицы не попадут в клетки с нулевой стоимостью. Это означает, что итоговое значение приведенной целевой функции будет равно нулю. Так как существует ограничение на неотрицательность переменных, нулевое значение целевой функции является оптимальным. Этап 2. Если некоторое решение является допустимым, то каждой строке и каждому столбцу соответствует только один элемент. Если процесс распределения элементов осуществляется только в клетки с нулевой стоимостью, он приведет к получению минимального значения целевой функции. 1. Найти строку, содержащую только одно нулевое значение стоимости, и в клетку, соответствующую данному значению, поместить один элемент. Если такие строки отсутствуют, допустимо начать с любого нулевого значения стоимости. 2. Зачеркнуть оставшиеся нулевые значения данного столбца. 3. Пункты 1 и 2 повторять до тех пор, пока продолжение описанной процедуры окажется невозможным. Если на данном этапе окажется, что есть несколько нулей, которым не соответствуют назначения и которые являются незачеркнутыми, то необходимо: 4. Найти столбец, содержащий только одно нулевое значение, и в соответствующую клетку поместить один элемент. 5. Зачеркнуть оставшиеся нули в данной строке. 6. Повторять пункты 4 и 5 до тех пор, пока дальнейшая их реализация окажется невозможной. Если окажется, что таблица содержит неучтенные нули, повторить операции 1-6. Если решение является допустимым, т.е. все элементы распределены в клетки, которым соответствует нулевая стоимость, то полученное решение одновременно является оптимальным. Если решение является недопустимым, осуществляется переход к этапу 3. Этап 3. 1. Провести минимальное число прямых через строки и столбцы матрицы (но не по диагоналям) таким образом, чтобы они проходили через все нули, содержащиеся в таблице. 2. Найти наименьший среди элементов, через которые не проходит ни одна из проведенных прямых. 3. Вычесть его из всех элементов, через которые не проходят прямые. 4. Прибавить найденный элемент ко всем элементам таблицы, которые лежат на пересечении проведенных ранее прямых 5. Все элементы матрицы, через которые проходит только одна прямая, оставить без изменения. В результате применения данной процедуры в таблице появляется по крайней мере один новый ноль. Необходимо возвратиться к этапу 2 и повторять алгоритм до тех пор, пока не будет получено оптимальное решение. Пример 1. Некоторая компания имеет четыре сбытовые базы и четыре заказа, которые необходимо доставить различным потребителям. Складские помещения каждой базы вполне достаточны для того, чтобы вместить один из этих заказов. В содержится информация о расстоянии между каждой базой и каждым потребителем. Как следует распределить заказы по сбытовым базам, чтобы общая дальность транспортировки была минимальной? Расстояние от сбытовых баз до потребителей:
Решение: Понимание существа проблемы можно в значительной степени облегчить, если перед тем, как применять Венгерский метод, попытаться решить поставленную задачу, используя один из широко известных методов. Примените метод Вогеля и проследите, насколько он приближает нас к оптимальному решению, которое мы рассмотрим в конце данного раздела. Значения общего спроса и общего предложения для всех строк и столбцов равны единице. Этап 1 Венгерского метода: В каждой строке находится наименьший элемент. Выявление наименьших элементов по строкам:
Наименьший элемент вычитается из всех элементов соответствующей строки Вычитание наименьшего элемента по строкам и выявление наименьшего элемента по столбцам:
Найденный наименьший элемент вычитается из всех элементов соответствующего столбца. Вычитание наименьшего элемента по столбцам:
В соответствии с процедурой, описанной в этапе 2, осуществляются назначения. Наличие назначения обозначается через
Назначения в клетки с нулевыми значениями:
На данном этапе мы можем осуществить только три нулевых назначения, тогда как требуемое их количество равно четырем. Полученное распределение является недопустимым. Переходим к этапу 3. Проводим наименьшее число прямых, проходящих через все нули таблицы. Проведение прямых через нулевые элементы:
Наименьшим элементом, через который не проходит ни одна из прямых, является число 2. Скорректируем таблицу так, как это описано выше в соответствии с этапом 3, т.е. вычтем 2 из каждого элемента, через который не проходит ни одна прямая, и добавим 2 ко всем элементам, лежащим на пересечении двух прямых, оставив без изменения все прочие элементы, через которые проходит только одна прямая. Теперь перераспределим соответствующие назначения сбытовых баз и потребителей. Скорректированная таблица с назначениями для нулевых клеток:
Теперь требование о размещении четырех назначений в клетки с нулевой стоимостью выполняется, следовательно, полученное решение является оптимальным. Перевозки осуществляются со сбытовой базы А к потребителю I, с базы В — к потребителю II, с базы С — к потребителю III и с базы D — к потребителю IV. Хотя данное решение и является оптимальным, однако оно не единственное. Тем не менее в любом оптимальном решении должен присутствовать маршрут (С,III), поскольку это единственный элемент с нулевой стоимостью в строке С. Два других оптимальных распределения назначений представлены ниже. Первое альтернативное оптимальное решение:
Второе альтернативное оптимальное решение:
Минимальную дальность перевозок для каждого из трех решений можно вычислить из исходной таблицы: Решение 1: 68 + 60 + 35 + 45 = 208 миль; Решение 2: 68 + 63 + 35 + 42 = 208 миль; Решение 3: 72 + 56 + 35 + 45 = 208 миль. Общая дальность перевозок для всех трех решений одинакова. Рассмотрим решение примера 1 с помощью средств табличного процессора. Введем на листе MS Excel данные как на рисунке 1. В окне Поиск решения (Сервис/Поиск решения) заполним поля как на рисунке 2 с учетом того, что в каждом пункте назначения объем потребности равен 1 и величина предложения каждого пункта производства равна 1. Значения в ячейках В12:G17 должны быть целыми, они могут принимать значения либо 1, либо 0. 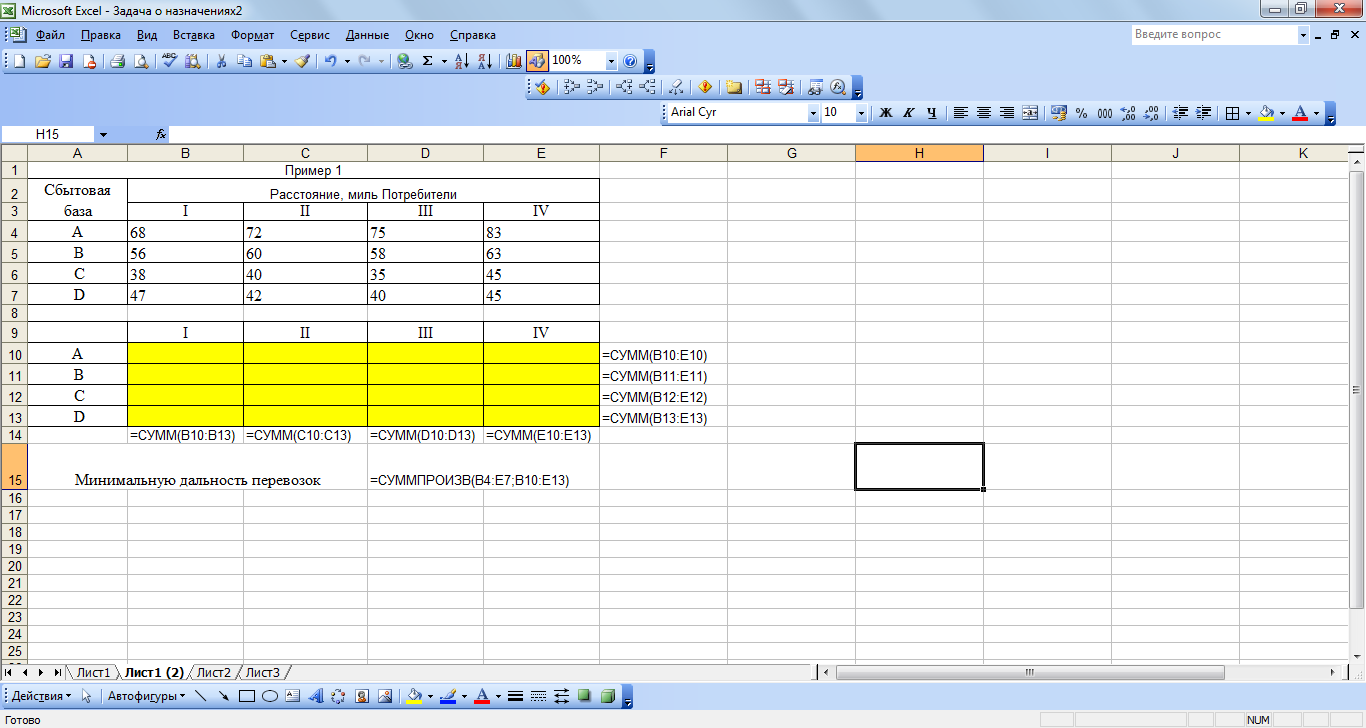 Рисунок 1 – Заполнение таблицы данными 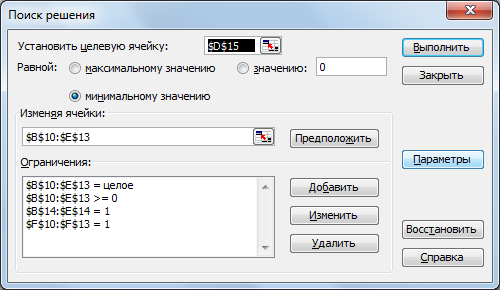 Рисунок 2 – Параметры окна надстройки Поиск решения 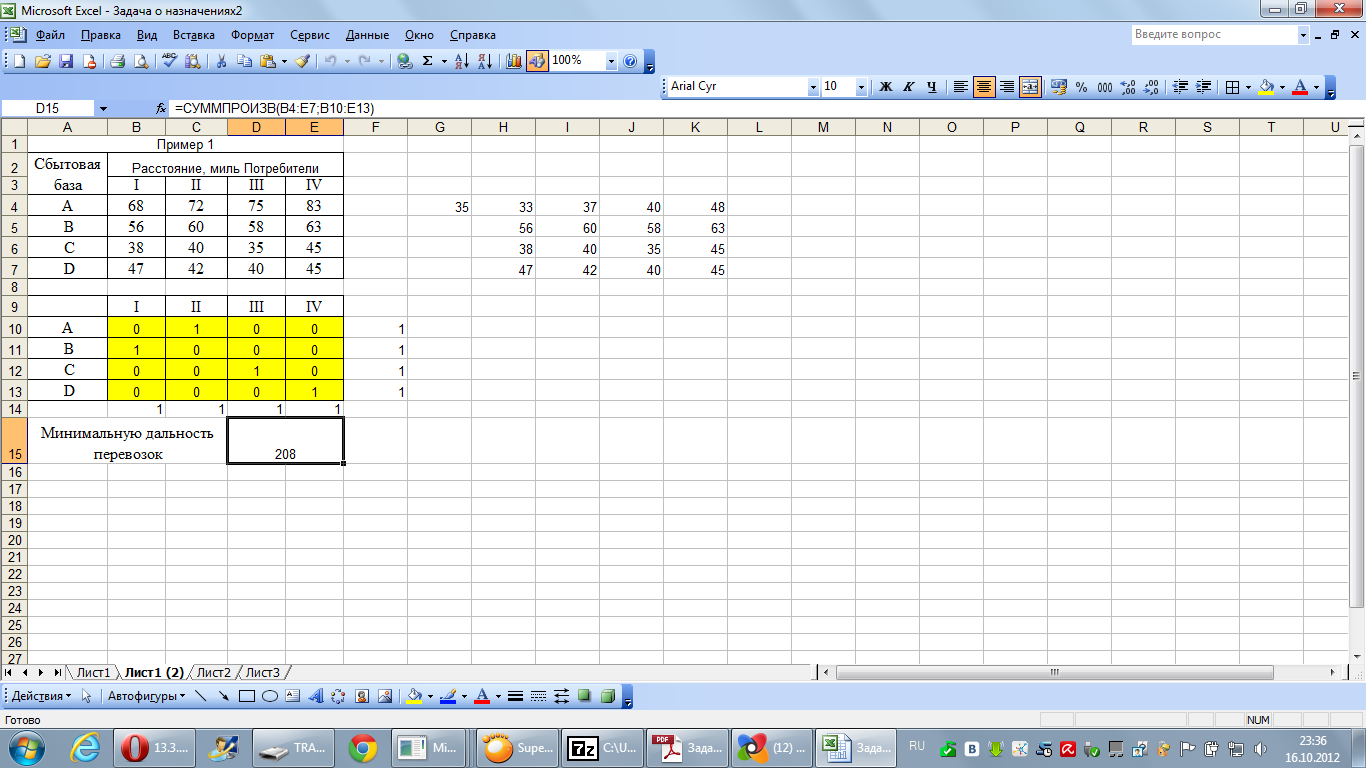 Рисунок 3 – Оптимальное решение, найденное с помощью надстройки Алгоритм решения задачи о назначениях предполагает минимизацию ее целевой функции. Если имеется задача о назначениях , целевую функцию которой нужно максимизировать, то поступают таким же образом, как и в алгоритме решения транспортной задачи: после окончания формирования первой таблицы все ее элементы умножаются на (— 1). Пример 2. В распоряжении некоторой компании имеется 6 торговых точек и 6 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца в каждой торговой точке. Результаты этой оценки представлены в таблице. Объемы продаж в различных торговых точках для различных продавцов
Как коммерческий директор должен осуществить назначение продавцов по торговым точкам, чтобы достичь максимального объема продаж? Решение. Все элементы исходной таблицы умножаются на (-1); Модификация исходных данных и выявление минимальных элементов
Минимальный (наибольший по абсолютной величине) элемент вычитается из всех элементов соответствующей строки. Вычитание минимального элемента по строкам и выявление минимальных элементов по столбцам
Минимальный элемент вычитается из всех элементов соответствующего столбца. Вычитание минимального элемента по столбцам
Дальнейший поиск оптимального решения осуществляется в соответствии с обычным алгоритмом Практическое задание. Самостоятельно решить пример 2 с помощью алгоритма Венгерского метода. Далее рассмотрим решение примера 2 с помощью средств табличного процессора. Введем на листе MS Excel данные как на рисунке 1. В окне Поиск решения (Сервис/Поиск решения) заполним поля как на рисунке 2 с учетом того, что в каждом пункте назначения объем потребности равен 1 и величина предложения каждого пункта производства равна 1. Значения в ячейках В12:G17 должны быть целыми, они могут принимать значения либо 1, либо 0. 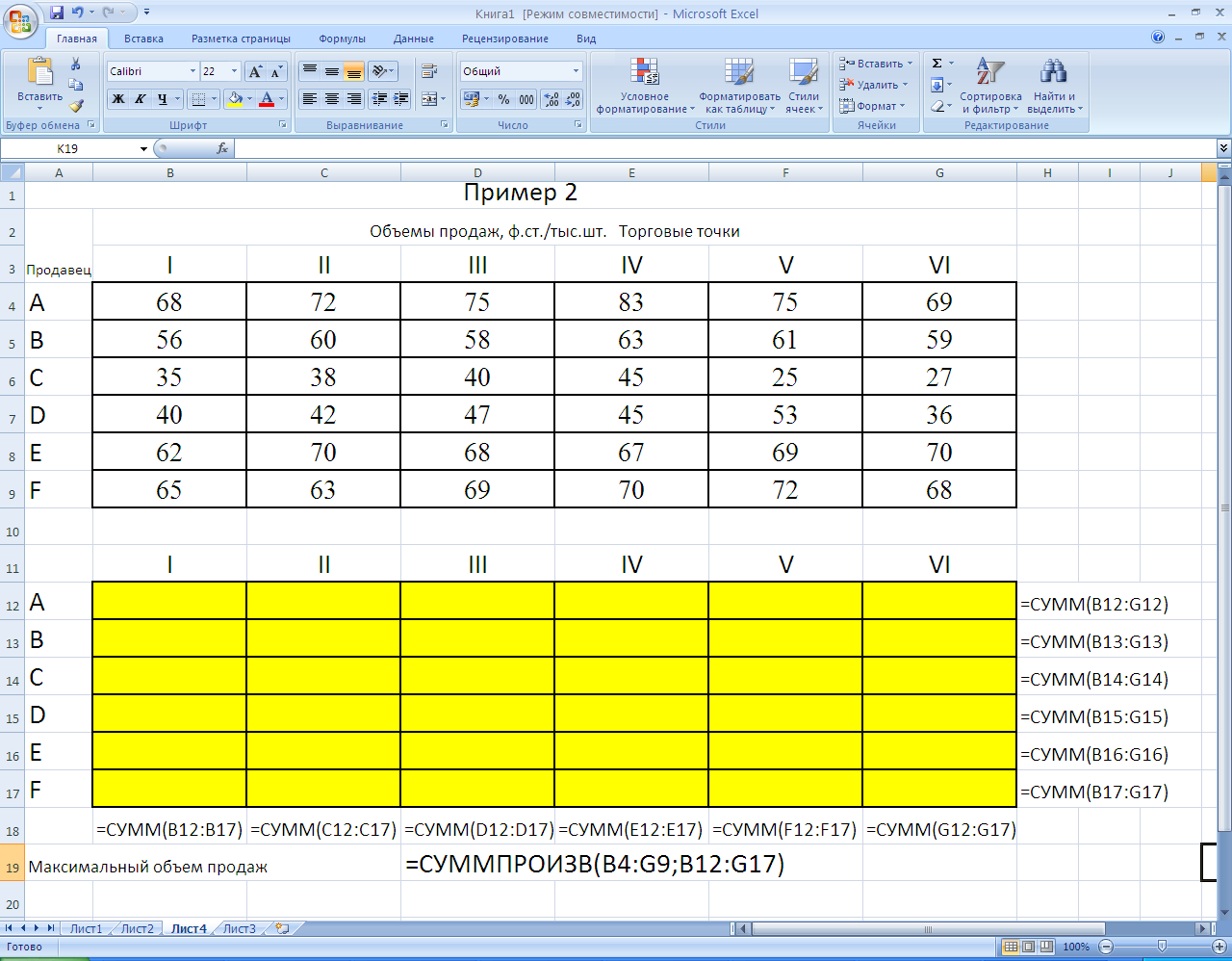 Рисунок 1 – Заполнение таблицы данными 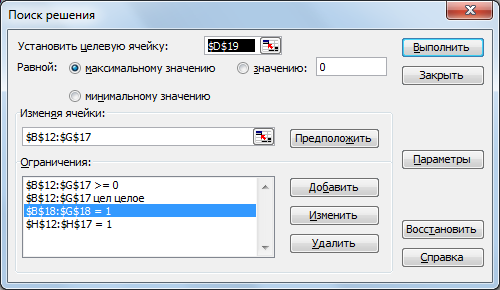 Рисунок 2 – Параметры окна надстройки Поиск решения 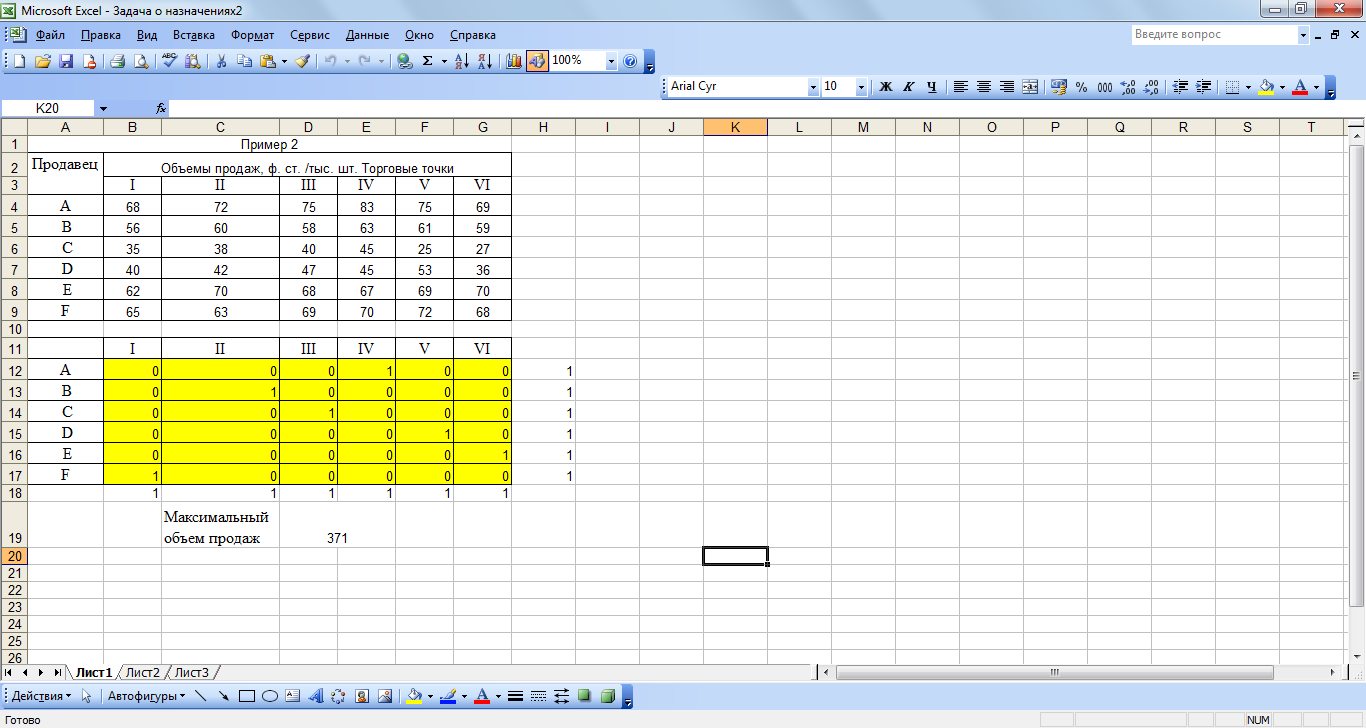 Рисунок 3 – Оптимальное решение, найденное с помощью надстройки Практическое задание на закрепление навыков решения задач о назначениях (с использованием алгоритма Венгерского метода и программными средствами) Задача 1. Решить задачу об оптимальном назначении с матрицей эффективностей A.  Задача 2. Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты первого проекта являются входными данными для второго проекта, выходные результаты второго проекта — это входные данные для третьего проекта, результаты третьего проекта используются для работы над четвертым проектом. В качестве научных руководителей проектов рассматриваются кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время, необходимое ему для реализации проекта. Матрица времен приведена ниже Для варианта 1
Для варианта 2
Контрольные вопросы Какова постановка задачи о назначениях? В чем отличие модели задачи о назначениях от модели ТЗ? Каковы исходные и искомые параметры задачи о назначениях? Запишите математическую модель задачи о назначениях. Как записать модель задачи о назначениях, подразумевающую максимизацию ЦФ? Каким образом в модели задачи о назначениях можно запретить конкретное назначение? В чем особенности процесса приведения задачи о назначениях к сбалансированному виду? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 0
0 7
7