инженерка. Практическая работа Задание
 Скачать 6.43 Mb. Скачать 6.43 Mb.
|
|
Практическая работа 1. Задание. Пусть в таблице даны координаты границ залежи. Строим график У (Х). Требуется определить площадь заштрихованной области.
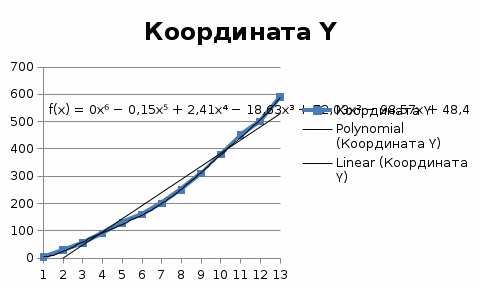 Используем математический пакет SMath Studio (Math CAD) для работы с матрицами и для применения МНК. 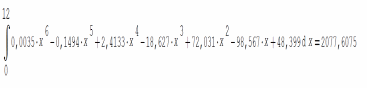 Практическая работа №2. Пусть в таблице даны координаты границ залежи. Строим график У (Х). Требуется определить площадь заштрихованной области.
1. По графику видно, что функция для интерполяции данных должна быть нелинейной. Рассмотрим в Excel две функции тренда – степенную и полиномиальную второй степени. Более точной является функция полинома (у нее степень доверия R^2=0,998). 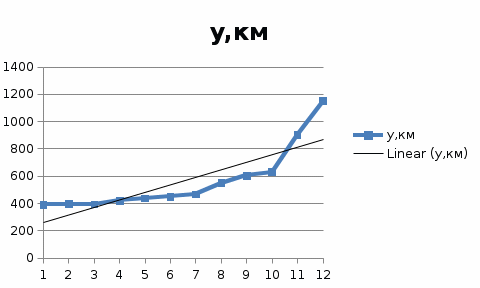 2. Но не забываем, что речь идет о приближенных численных методах, поэтому необходимо рассматривать несколько вариантов вычислений, из которых выбираем самый точный. Поэтому используем матричный МНК и программную среду Math CAD/SMath Studio для вычисления коэффициентов полинома второй степени Умнк=а+в*Х+с*Х^2. В матрице Х три столбца: с единицами, с Х и с Х^2. Получаем а=397,6576; в=-4,8432 ;с=0,9969.  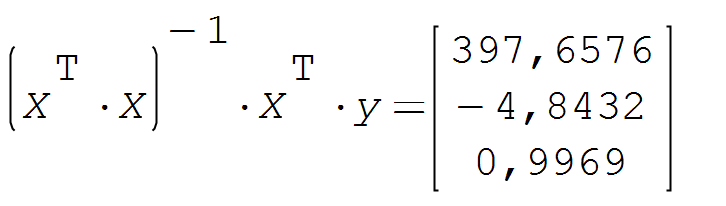 3. Вычислим в Math CAD/SMath Studio определенный интеграл от функции, полученной МНК. Это будет эталонное значение. 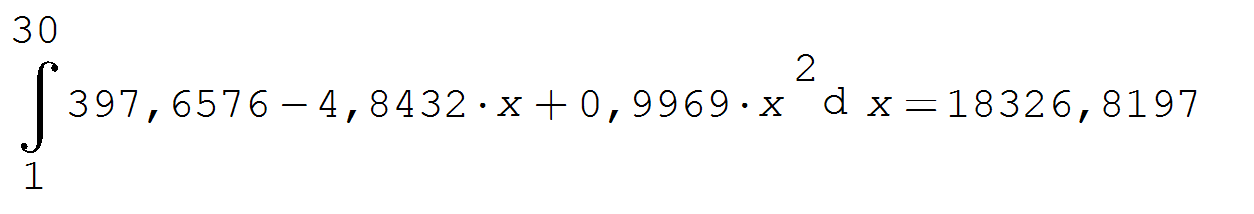 Практическая работа №3. 1. Вычислим площадь методом трапеций (***) в Excel.
Практическая работа №4. 1.Даны координаты залегания двух пород в одной плоскости с разными характеристиками. Определить есть ли соприкосновение пород, если да, то определить координаты.
1. Строим графики У1 и У2. 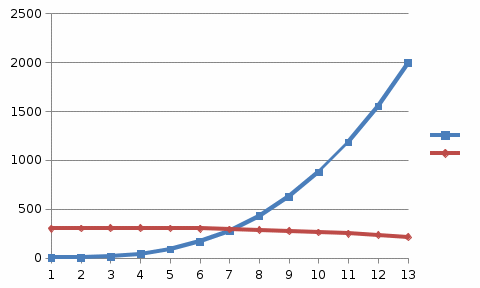 2. По графикам видно, что есть одна общая точка пересечения. Что бы ее найти, необходимо вычислить разность координат У3=У2-У1 и решить уравнение У3=0.
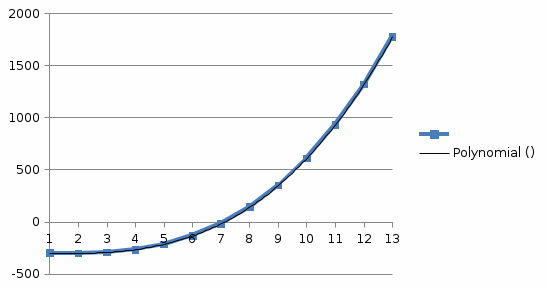 3. По правилу дихотомии – корень У3=0 находится на том отрезке, на концах которого функция У3 принимает разные по знаку значения. В нашем примере в точке Х=6 У3=+16; в точке Х=7 У3=-143. (Строки в таблице выделены желтым). 4. График У3 нелинейный, скорее всего функция представляет собой полином третьей степени. Убедимся в этом с помощью тренда в Excel. Но как мы уже убедились, табличный метод наименьших квадратов (МНК) более точен, и с его помощью мы и найдем математическое выражение функции У3. Для этого в Math CAD/Smath Studio вводим столбец значений У3 и матрицу Х, где первый столбец только 1; второй столбец – это Х; третий столбец – Х^2; третий – Х^3. 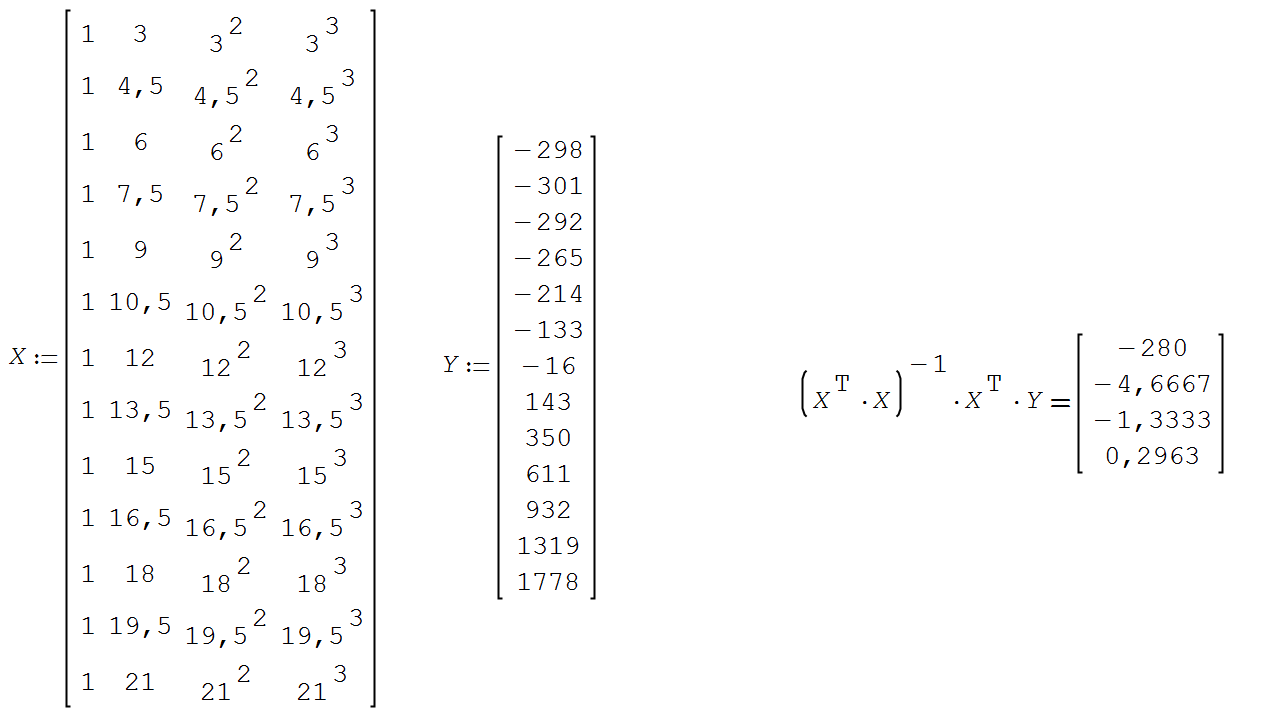 контура пересекаются Х= 12,1. 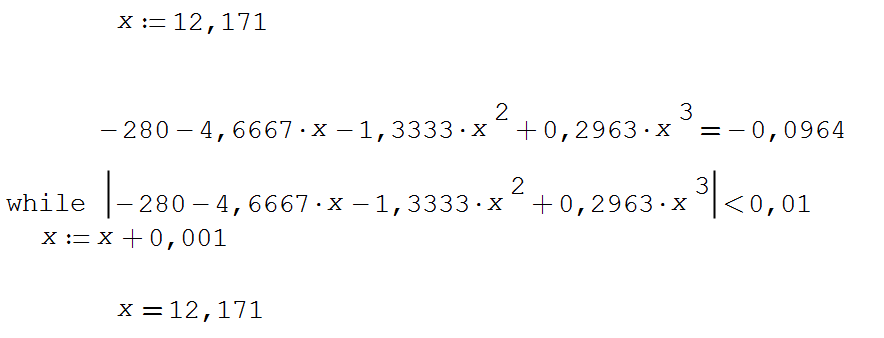 Практическая работа №5. 
Используем математический пакет SMath Studio (Math CAD) для работы с матрицами и для применения МНК. 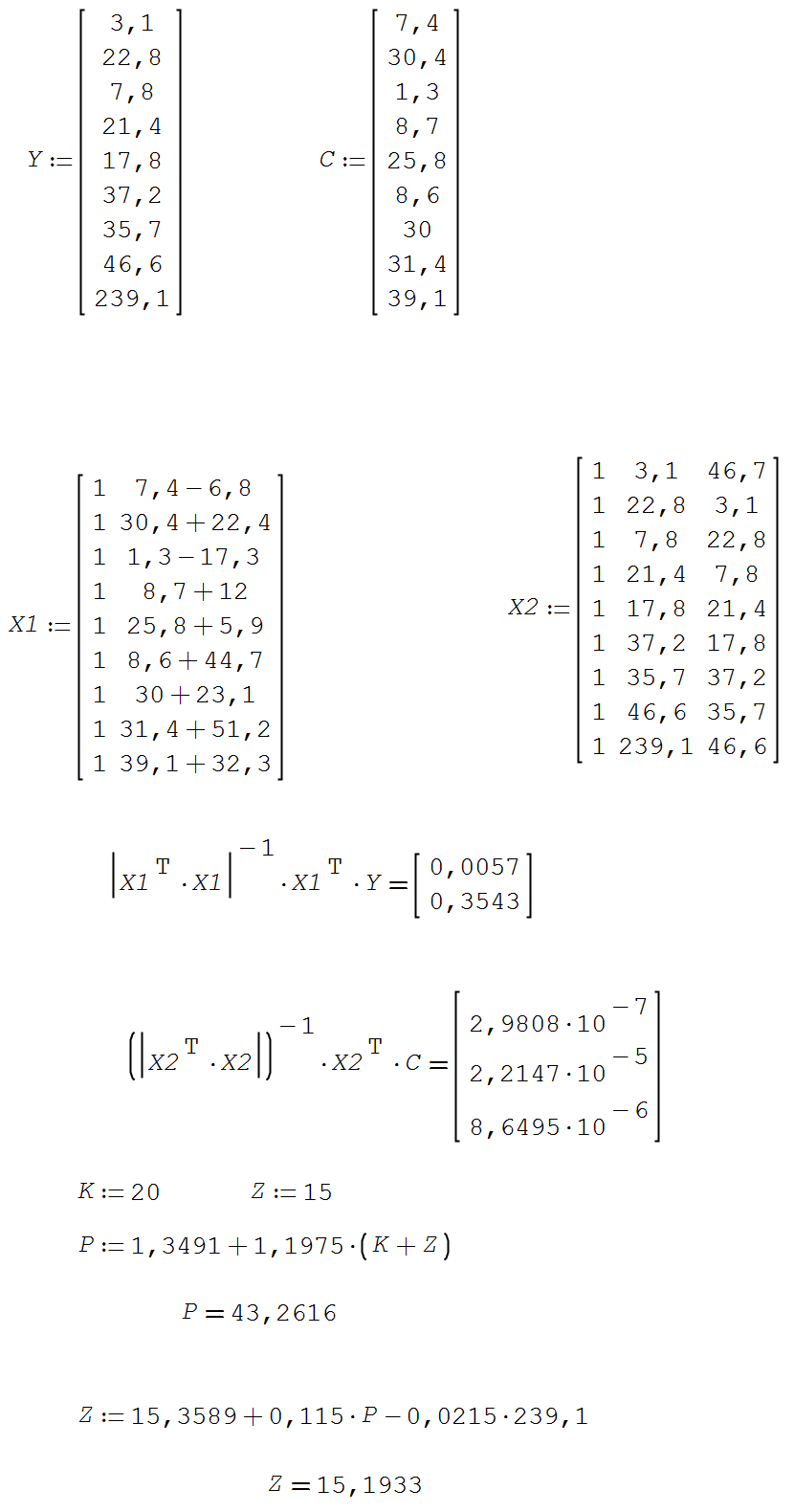 В результате применение численных методов по статистической информации определили формулы в зависимости производства и качества продукции от уровня обновления оборудования и результата производства в предыдущий период решили приближённо систему данных уравнении и получили что при достижений качество продукций на 20% требуется обновления оборудования на 15%. Производительность будет 43.   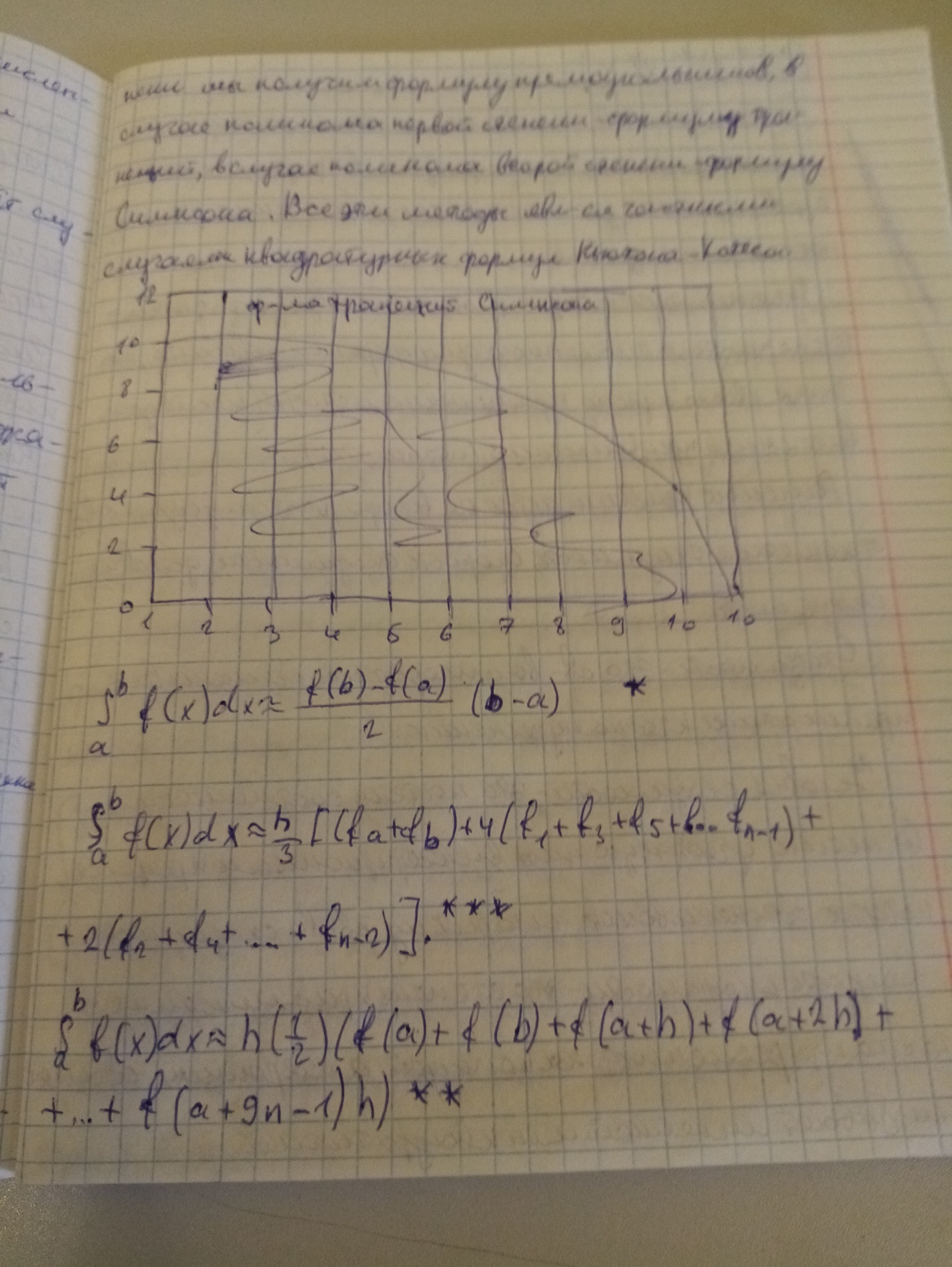      | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
