Инвестиционный анализ. Пр№1 Инвест анализ Кожанова ДД М19М571. Практических заданий по дисциплине инвестиционный анализ
 Скачать 117.19 Kb. Скачать 117.19 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ИНВЕСТИЦИОННЫЙ АНАЛИЗ Группа М19М571 Студент Кожанова Д.Д. МОСКВА 2022 г Задания для самостоятельной работы. Задача № 1. Определить, какая из ценных бумаг является более привлекательной с точки зрения минимизации риска. По акциям компании А ожидается доходность в размере 7–12–22% с вероятностью ее получения соответственно 30–40–30%, по акциям компании B ожидается доходность 10–15–22% годовых с вероятностью 20–30 – 50% соответственно. Ответ: Для того, чтобы определить, какая из ценных бумаг является более привлекательной с точки зрения минимизации риска необходимо оценить вероятностное распределение доходности, для чего рассчитывается коэффициент вариации доходности (СV): CV=σd, где – стандартное отклонение доходности ценной бумаги (d) от ее наиболее вероятной (ожидаемой) доходности d, % Стандартное отклонение доходности i-й ценной бумаги: σ=i=1n(di-d)2*pi Ожидаемая величина доходности: d=i=1ndi*pi, где di – прогнозные оценки значений доходности по i-й ценной бумаге, %; Pi – вероятность получения дохода в i-й экономической ситуации, коэф. Рассчитаем для каждой компании: А: d=7*0,3+12*0,4+22*0,3=13,5 % В: d=10*0,2+15*0,3+22*0,5=17,5% А: σ=7-13,52*0,3+12-13,52*0,4+22-13,52*0,3=5,94 В: σ=10-17,52*0,2+15-17,52*0,3+22-17,52*0,5=4,82 А: CV=5,94*100%13,5=43,98% В: CV=4,82*100%17,5=27,55% Ответ: менее рискованна покупка акций В, при этом средняя ожидаемая доходность акций В также значительно выше средней ожидаемой доходности акций А. Задача №5. Определить уровень риска портфеля, включающего следующие активы: 2% акции компании А, имеющие β = 1,8; 60% акции компании В, имеющие β = 0,8; 30% акции компании С, имеющие β = 1; 8% акции компании D, имеющие β = 1,1. Ответ: Β = 0,02*0,18+0,6*0,08+0,3*0,01+0,08*0,11 = 0,0634 Вывод: риск велик и доходность не велика, так как основная масса по % имеет невысокий показатель рынка. Задача №4. Определить ковариацию и коэффициент корреляции для активов А и B, статистика доходности которых представлена в таблице:
Решение: Коэффициент корреляции рассчитывается по формуле. Расчёты представлены ниже на рисунке №1. 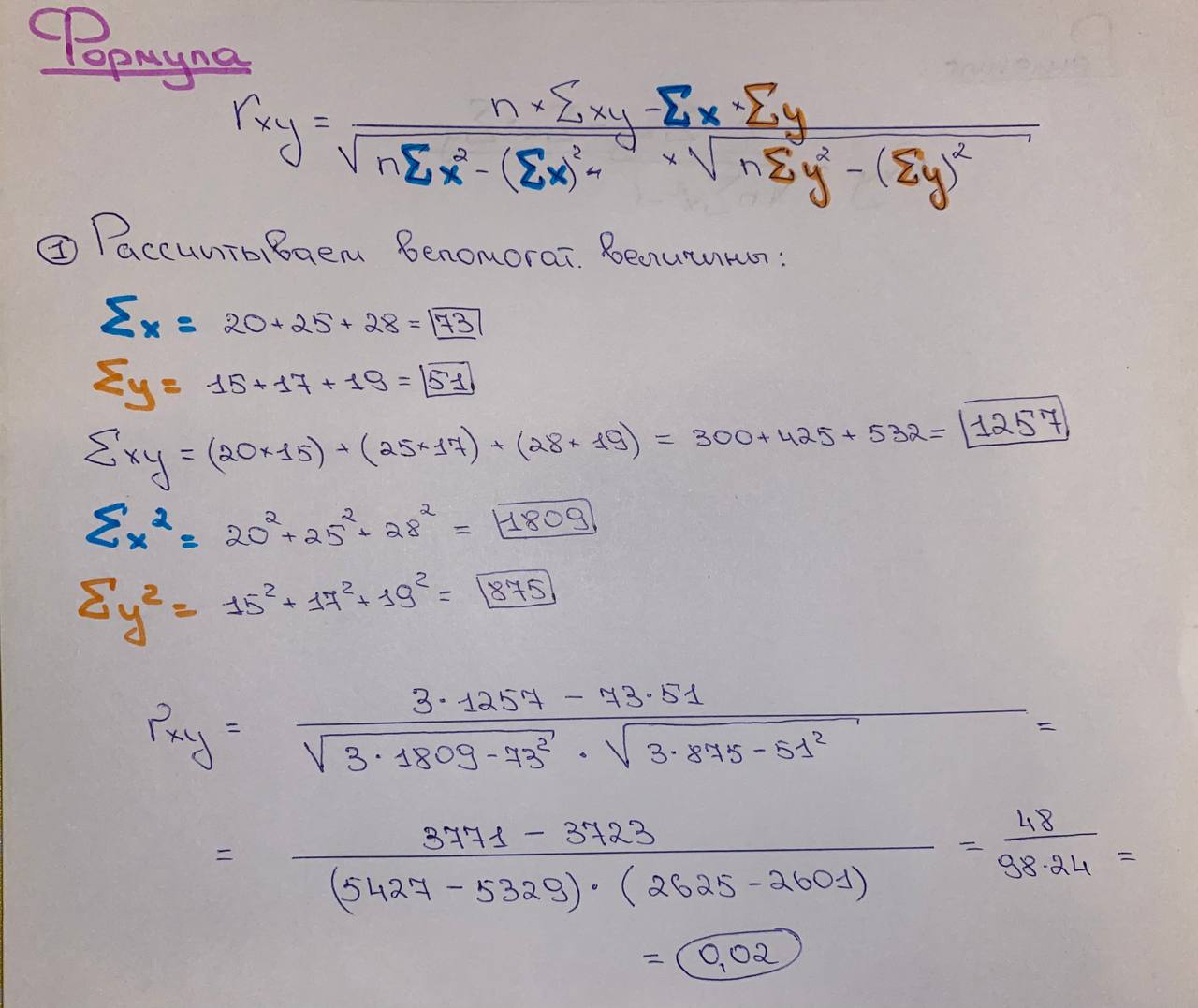 Рисунок №1. Расчёты коэффициента корреляции. Абсолютная величина R(ху) лежащая между 0 и 1, служит мерой тесноты. В зависимоти от величины r(ху) можно сделать следующие заключения о степени тесноты вязи: 0<= R(xy)< - 0,2 – практически нет связи. Ответ: В данном случае между доходностями А и В отсутствует сильная связь. |
