Практика 1. Практических занятий

• Название: Практических занятий
• Анкор: Практика 1
• Дата: 27.09.2021
• Размер: 0.63 Mb.
• Имя файла: prаkticheskie_zаnjatija.doc
• Тип: Задача; #237701
• страница: 3 из 4

Задача № 5.

Решить задачу №4 при условиях t ₁= 10 ⁰С, j₁= 40%, t ₂= 80 ⁰С, t₃= 40 ⁰С.
Тема № 10. Истечение газов и паров.
Задача № 1.

Воздух из резервуара с постоянным давлением р₁ = 10 МПа и температурой t₁ = 15 ⁰С вытекает в атмосферу через трубку с внутренним диаметром 10 мм.

Найти скорость истечения воздуха и его секундный расход, если наружное давление равно р₂ = 0,1 МПа. Процесс расширения воздуха считать адиабатным.

Решение: Определяем отношение , что меньше критического отношения давлений для воздуха, составляющего 0,528. Скорость истечения будет равна критической и определится

м/с.

Секундный расход , где м², м³/кг.

Следовательно,

кг/с.
Задача № 2.

Определить теоретическую скорость адиабатного истечения воздуха через сопло Лаваля, если р₁ = 0,8 МПа, t₁ = 20 ⁰С, а давление среды на выходе из сопла р₂ = 0,1 МПа. Сравнить полученную скорость с критической.
Задача № 3.

Определить теоретическую скорость истечения пара из котла в атмосферу. Давление пара в котле р₁ = 1,2 МПа, температура t ₁= 300 ⁰С. Процесс расширения пара считать адиабатным. Барометрическое давление принять равным р₂ = 100 кПа.

Решение: Отношение давлений р₂ / р₁= 1/12 = 0,0834, т.е. оно меньше критического отношения давлений для перегретого пара, составляющего 0,546, поэтому скорость истечения будет равна критической скорости.

Для перегретого пара

, м/с.

Для нахождения i_кр определим Р_кр:

МПа.

Для определения используем iSдиаграмму. Проведя адиабату от точки, характеризующей Р₁ = 1,2 МПа и t ₁= 300 ⁰С до изобары

р_2кр= 0,66 МПа, получаем = 148 кДж/кг и таким образом,

м/с.
Задача № 4.

Решить задачу № 3 при условии, что истечение пара происходит через сопло Лаваля.
Тема № 11. Процессы в компрессорах.
Задача № 1.

Компрессор всасывает 100 м³/ч воздуха при давлении р₁ = 0,1 МПа и температуре t ₁= 27 ⁰С. Конечное давление воздуха составляет р₂ = 0,8 МПа. Найти теоретическую мощность двигателя привода компрессора и расход охлаждающей воды, если температура ее повышается на 13 ⁰С. Расчет произвести для изотермического, адиабатного и политропного сжатия. Показатель политропы n = 1,2, теплоемкость воды С = 4,19 кДж/(кг ⁰С).

Решение: 1. Изотермическое сжатие.

Работа компрессора

МДж/ч.

Теоретическая мощность двигателя

кВт.

Теплоту, отводимую с охлажденной водой, находим из равенства 20,8 МДж. Следовательно, расход охлаждающей воды

кг/ч.

2. Адиабатное сжатие.

Работа компрессора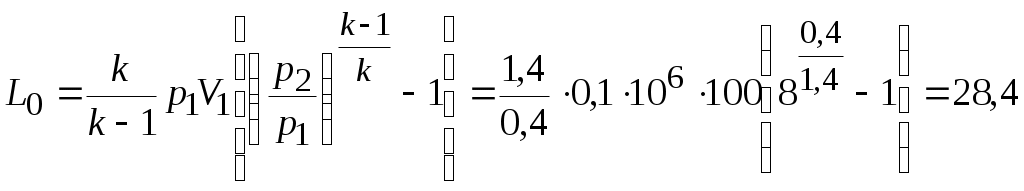

МДж/ч.

Мощность двигателя кВт.

3. Политропное сжатие.

Работа компрессора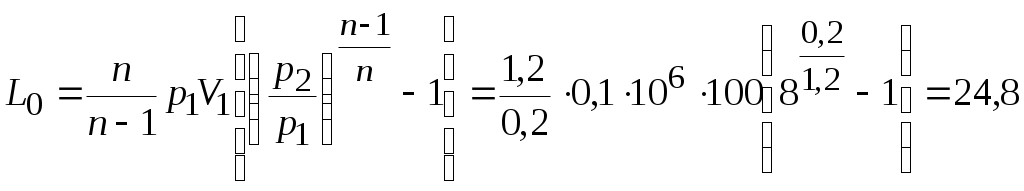

МДж.

Мощность двигателя кВт.

Количество теплоты, отводимой от воздуха, находим по уравнению

.

Здесь: = 0,723 кДж/(кг⁰С) – массовая изохорная теплоемкость.

Массовый расход воздуха кг/ч.

Температура воздуха в конце сжатия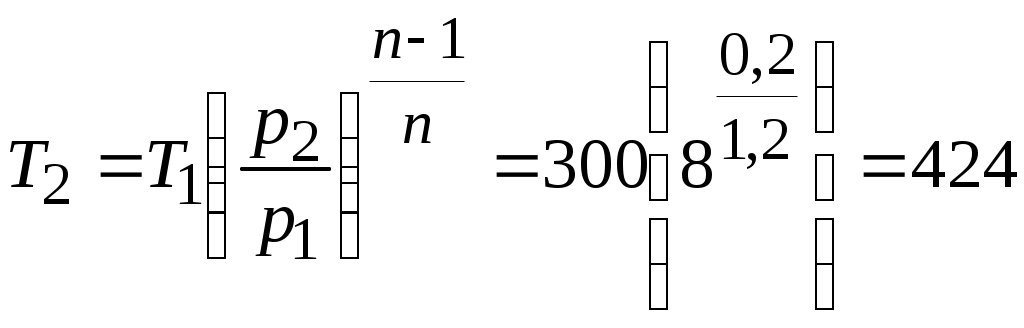

К.

Таким образом, кДж/ч.

Расход охлаждающей воды кг/ч.
Задача № 2.

Решить задачу № 1 при р₁ = 0,2 МПа, t ₁= 30 ⁰С, р₂ = 1 МПа, n = 1,25.
Задача № 3.

Воздух при давлении р₁ = 0,1 МПа и температуре t ₁= 20 ⁰С должен быть сжат по адиабате до давления р₂ = 0,8 МПа. Определить температуру в конце сжатия, теоретическую работу компрессора и величину объемного к.п.д.:

а) для одноступенчатого компрессора;

б) для двухступенчатого компрессора с промежуточным холодильником, в котором воздух охлаждается до начальной температуры. Относительная величина вредного пространства а = 8%. Полученные результаты сравнить между собой.

Решение: 1. Одноступенчатое сжатие.

Температура в конце сжатия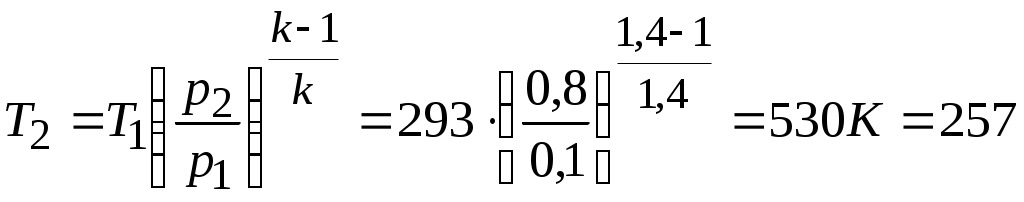

⁰С.

Теоретическая работа компрессора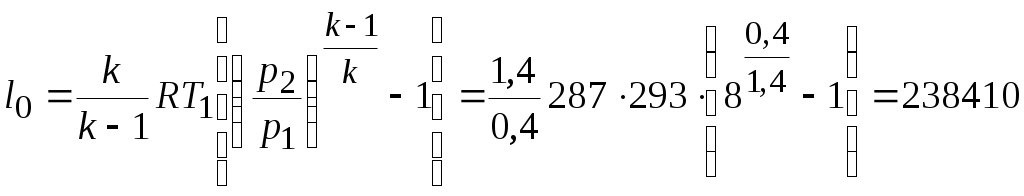

Дж/кг

Объемный к.п.д. компрессора .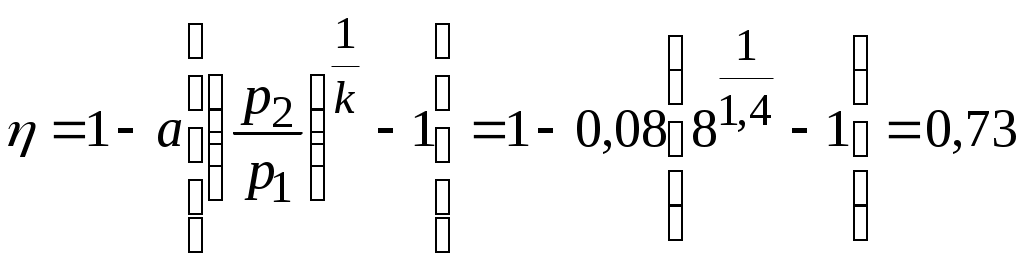

2. Двухступенчатое сжатие.

Степень сжатия в каждой ступени . Температура в конце сжатия в каждой ступени 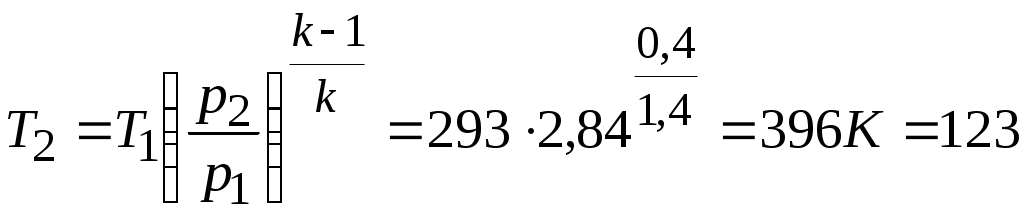⁰С.

Теоретическая работа компрессора в обеих ступенях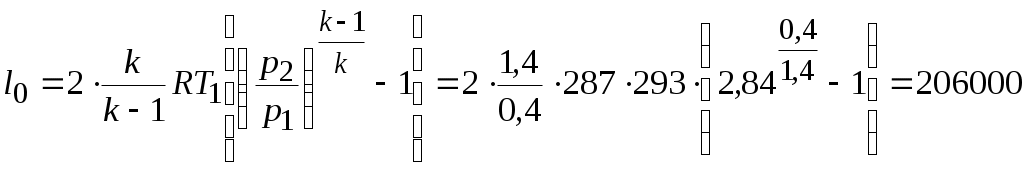

Дж/кг.

Объемный к.п.д. компрессора

Сравнение результатов расчетов показывает, что при двухступенчатом сжатии меньше температура воздуха в конце сжатия и теоретические затраты работы и выше объемный к.п.д. компрессора.
Задача № 4.

Решить задачу № 3 при следующих данных: р₁ = 0,15 МПа, t₁ = 25 ⁰С,

р₂ = 1 МПа, а = 9%.
Тема № 12. Циклы тепловых двигателей.
Задача № 1.

Для теоретического цикла поршневого двигателя внутреннего сгорания со смешанным подводом теплоты определить параметры состояния характерных точек цикла, полезную работу и термический к.п.д. по заданным значениям начального давления р₁ = 97 кПа и температуры t ₁= 27 ⁰С, степени сжатия  = 15, степень повышения давления λ = 1,7, степени предварительного расширения  = 1,3. Рабочим телом считать воздух, полагая теплоемкость постоянной. Изобразите цикл ДВС в – и TS– диаграммах. Определить также к.п.д. цикла Карно, проведенного в том же интервале температур t₁– t₄, что и цикл ДВС.

Решение: Изобразим цикл ДВС в 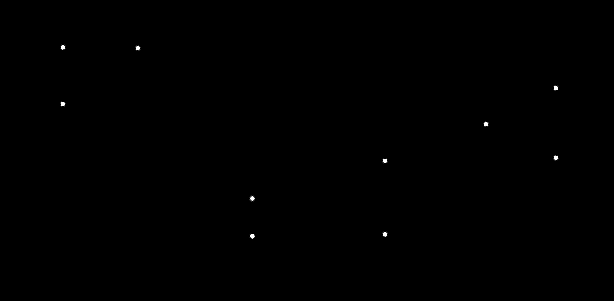– и TS– диаграммах.



1–2 – процесс адиабатного сжатия; 2–3 – подвод теплоты при ;

3–4 – подвод теплоты при ; 4–5 – адиабатное расширение;

5–1 – отвод теплоты при .

Параметры точки 1.

Давление р₁ = 97 кПа, температура Т₁= 273+27 = 300 К. Удельный объем найдем из уравнения состояния , где R= 287 Дж/кг· ⁰С – газовая постоянная воздуха.

м³/кг.

Параметры точки 2.

Степень сжатия , поэтому м³/кг.

Температура в конце адиабатного сжатия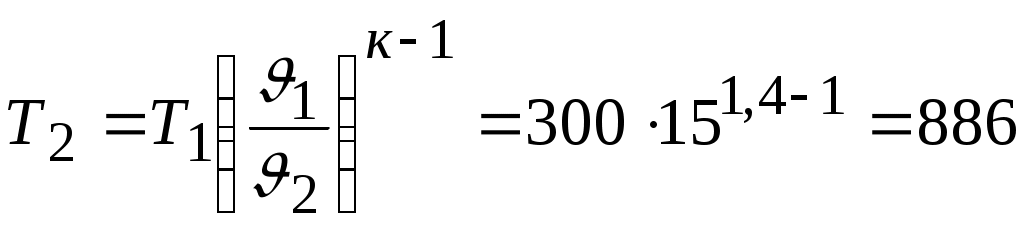

К.

Давление в конце адиабатного сжатия

кПа.

Параметры точки 3.

Удельный объем м³/кг.

Степень повышения давления , поэтому абсолютное давление

кПа.

Для идеального газа по закону Шарля , поэтому абсолютная температура К.

Параметры точки 4.

Абсолютное давление кПа.

Степень предварительного расширения , поэтому удельный объем м³/кг.

По закону Гей – Люссака для идеального газа , поэтому абсолютная температура Т₄= 1,31506 = 1958 К.

Параметры точки 5.

Удельный объем м³/кг.

Давление в конце адиабатного расширения определим из уравнения адиабаты 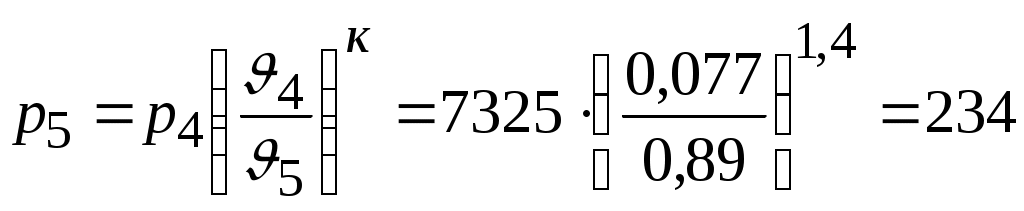, отсюда

кПа.

По закону Шарля , отсюда абсолютная температура

К.

Работа цикла определяется как разность между работой расширения и работой сжатия.

Работа сжатия

кДж/кг.

Работа расширения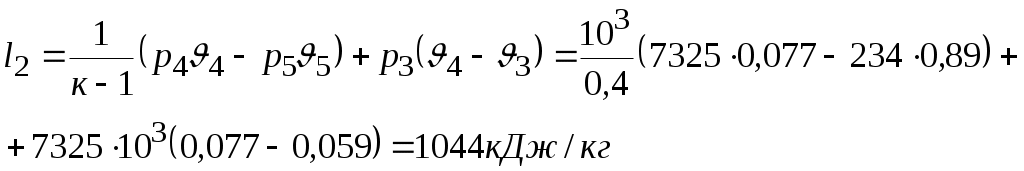



Работа цикла есть алгебраическая сумма l₁ и l₂

кДж/кг.

Количество подведенной теплоты:

в процессе 2–3 кДж/кг;

в процессе 3– 4 кДж/кг.

Количество отведенной теплоты

кДж/кг.

Телота, полезно непользуемая в цикле

кДж/кг.

Термический к.п.д. цикла

.

Термический к.п.д. цикла Карно по условиям задачи

.
Задача № 2.

Решить задачу № 1 при условиях: р₁ = 95 кПа, t₁ = 40 ⁰С, e = 16, r = 1,5,

= 1,5.
Задача № 3.

Для идеального цикла ГТУ с подводом теплоты при р = const определить параметры характерных точек, работу расширения, сжатия и полезную, количество подведенной и отведенной теплоты, термический к.п.д. цикла. Начальные параметры рабочего тела р₁ = 1 бар; Т₁ = 300 К; степень увеличения давления в компрессоре ; показатель адиабаты к = 1,4. Температура в точке 3 не должна превышать 1000К; рабочее тело – воздух; теплоемкость воздуха постоянная; расчет проводится на 1 кг. рабочего тела.

Решение: Удельный объем рабочего тела в точке 1

м³/кг.

Параметры точки 2: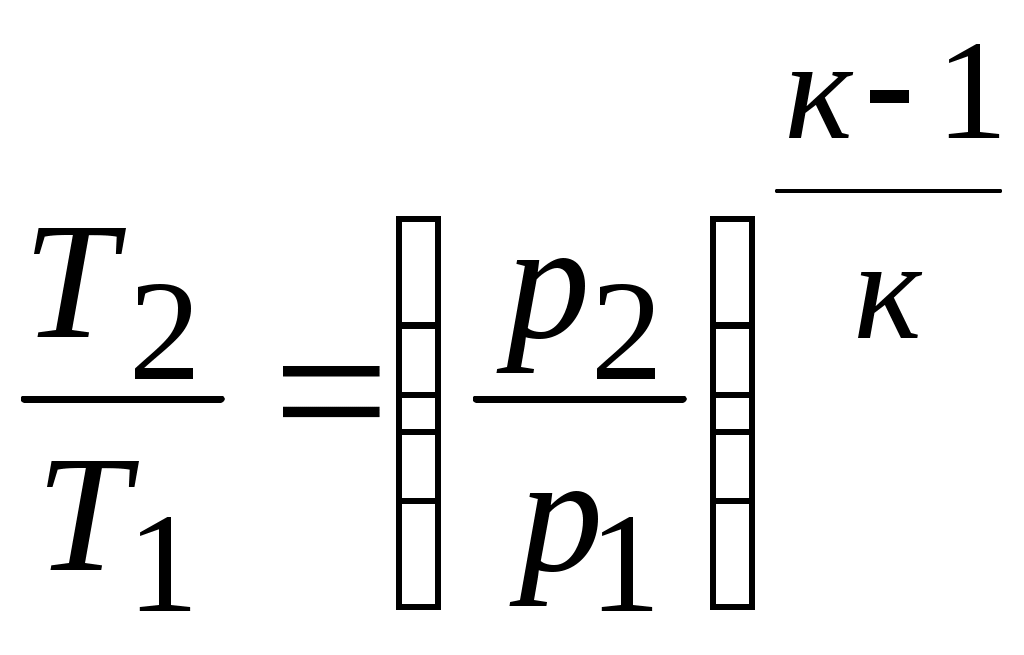

бар, ; К;

м³/кг.

Параметры точки 3:

р₃ = 10 бар, Т₃ = 1000 К, м³/кг.

Параметры точки 4:

р₄ = 1 бар, 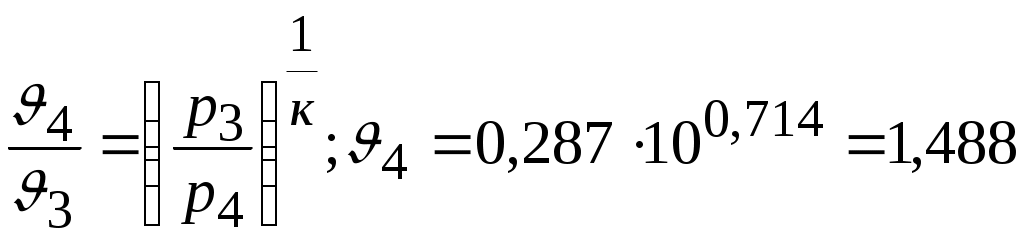м³/кг; К.

Работа сжатия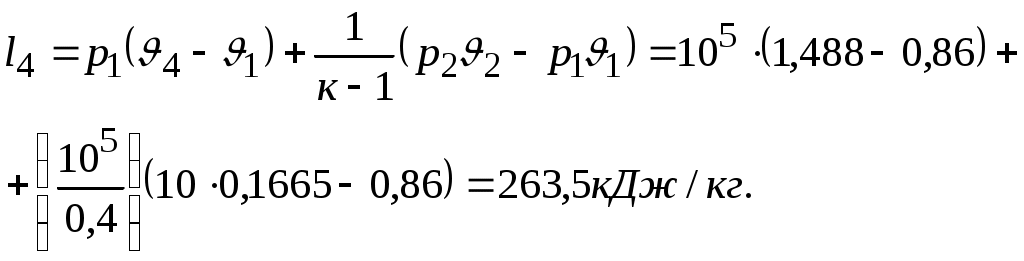



Работа расширения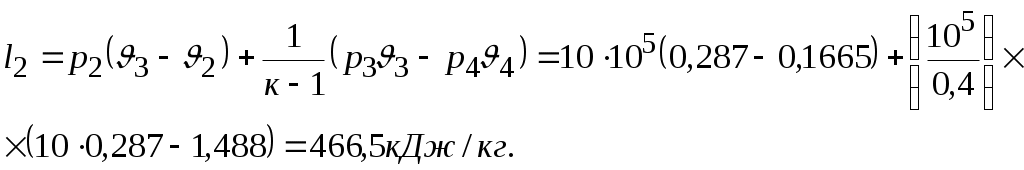



Полезная работа кДж/кг.

Количество подведенной теплоты

кДж/кг.

Количество отведенной теплоты

кДж/кг.

Полезно использованная теплота

q= 424-220 = 204 кДж/кг.

Термический к.п.д. цикла равен 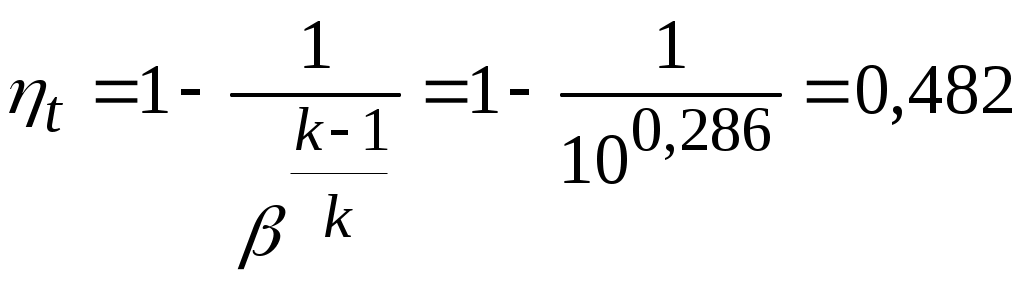или .