Практика 1. Практических занятий

• Название: Практических занятий
• Анкор: Практика 1
• Дата: 27.09.2021
• Размер: 0.63 Mb.
• Имя файла: prаkticheskie_zаnjatija.doc
• Тип: Задача; #237701
• страница: 2 из 4

Задача № 5.

1кг. воздуха при температуре t₁= 30 ⁰C и начальном давлении р₁= 0,1 МПа сжимается изотермически до конечного давления р₂ = 1 МПа. Определить конечный объем, затрачиваемую работу и количество теплоты, отводимой от газа.

Решение: Начальный объем воздуха найдем из уравнения состояния

0,87 м³/кг.

Так как в изотермическом процессе , то конечный объем

0,087 м³/кг.

Работа, затрачиваемая на сжатие 1кг. воздуха

= -200 кДж/кг.

Количество теплоты, отводимой от газа, равно работе, затраченной на сжатие, т.е.q= - 200 кДж/кг.
Задача № 6.

Воздух в количестве 0,5 кг. при p₁= 0,5 МПа и t₁= 30 ⁰С расширяется изотермически до пятикратного объема. Определить работу, совершенную газом, конечное давление и количество теплоты, сообщаемой газу.
Задача № 7.

1 кг. воздуха при начальной температуре t₁= 30 ⁰С и давлении p₁ = 0,1 МПа сжимается адиабатно до конечного давления p₂= 1 МПа. Определить конечный объем, конечную температуру и затрачиваемую работу.

Решение: Из соотношения параметров в адиабатном процессе имеем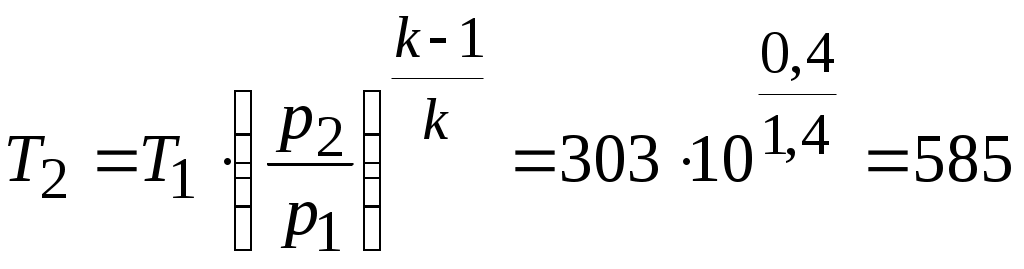

К

где = 1,4 – показатель адиабаты воздуха.

Затраченная работа кДж/кг.

Конечный объем м³/кг.
Задача № 8.

Воздух при давлении р₁= 0,45 МПа, расширяясь адиабатно до р₂= 0,12МПа, охлаждается до t₂= - 45 ⁰С. Определить начальную температуру и работу, совершенную 1 кг. воздуха.
Задача № 9.

1,5 кг. воздуха сжимается политропно от p₁= 0,09 МПа и t₁= 18 ⁰С до

p₂= 1 МПа, а температура при этом повышается до t₂= 125 ⁰С. Определить показатель политропы, конечный объем, затраченную работу и количество отведенной теплоты.

Решение: Показатель политропы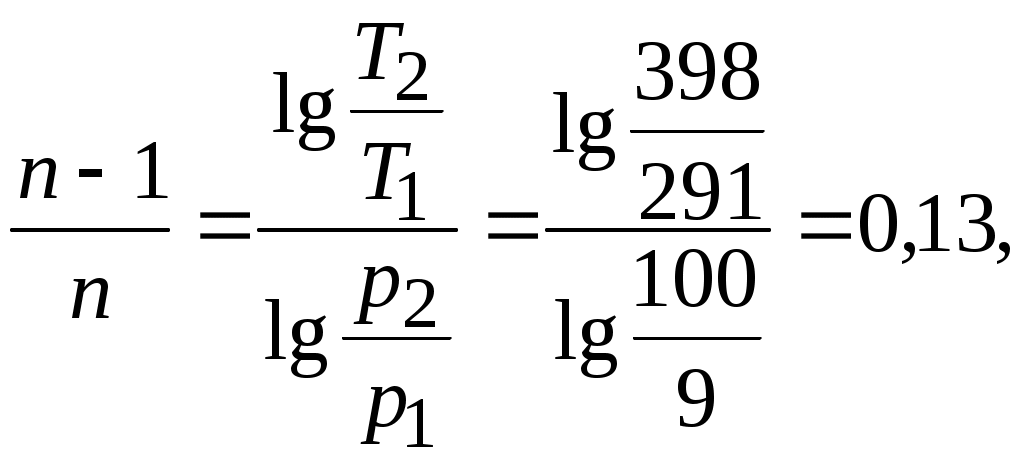



Конечный объем м³.

Затраченная работа

кДж.

Количество отведенной теплоты

кДж.
Задача № 10.

1 кг. воздуха при p₁ = 0,5 МПа и t₁= 111 ⁰С расширяется политропно до давления p₂ = 0,1 МПа. Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенной теплоты и полученную работу, если показатель политропы n = 1,2.
Тема № 7. Второй закон термодинамики.
Задача № 1.

Определить энтропию 1 кг. кислорода при p= 0,8 МПа и t= 250 ⁰С. Теплоемкость считать постоянной.

Решение: Энтропия .

Здесь: – изобарная теплоемкость,

–газовая постоянная,

p_н = 0,1013 Па –абсолютное давление при нормальных условиях.

кДж/(кг⁰С).
Задача № 2.

Определить энтропию 6,4 кг. азота при p= 0,5 МПа и t= 300 ⁰С. Теплоемкость считать постоянной.
Задача № 3.

1 кг. кислорода при температуре t₁ = 127 ⁰С расширяется до пятикратного объема, температура его при этом падает до t₂= 27 ⁰С. Определить изменение энтропии, считая теплоемкость постоянной.
Задача № 4.

10 м³ воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400 ⁰С. Сжатие производится: 1) изохорно; 2) изобарно; 3) адиабатно; 4) политропно с показателем политропы n = 2,2.

Принимая теплоемкость постоянной, найти энтропию воздуха в конце каждого процесса.
Задача № 5.

В сосуде объемом 300 л заключен воздух при давлении p₁ = 5 МПа и температуре t₁ = 20 ⁰С. Параметры среды: p₀ = 0,1 МПа, t₀ = 20 ⁰С.

Определить максимальную полезную работу, которую может произвести сжатый воздух, находящийся в сосуде.

Решение: Так как температура воздуха в начальном состоянии равна температуре среды, то максимальная работа, которую выполнить воздух, может быть получена лишь при условии изотермического расширения воздуха от начального давления p₁ = 5 МПа до давления среды p₂ = 0,1 МПа.

.

Определим массу воздуха, находящегося в сосуде, и объем воздуха после изотермического расширения:

кг, м³.

Поскольку изменение энтропии в изотермическом процессе

то

= 4377кДж
Задача № 6.

В сосуде объемом 200 л находится углекислый газ при температуре t₁= 20 ⁰С и давлении p₁= 10 МПа. Температура среды t₀= 20 ⁰С, давление среды p₀= 0,1 МПа.

Определить максимальную полезную работу, которую может произвести находящийся в сосуде газ.
Тема № 8. Водяной пар.
Задача № 1.

Определить состояние водяного пара, если его давление р = 0,5 МПа, а температура t= 172 ⁰С.

Решение: Из таблиц водяного пара давлению 0,5 МПа соответствует температура насыщенного пара t_н= 151,8 ⁰С. Следовательно, пар перегретый и перегрев составляет t-t_н= 172- 151,8 = 20,2 ⁰С.
Задача № 2.

Определить состояние водяного пара, если его давление р= 0,6 МПа, а удельный объем υ= 0,3 м³/кг.
Задача № 3.

Определить энтальпию и внутреннюю энергию влажного насыщенного пара при р= 1,3 МПа и степени сухости пара x = 0,98.

Решение: Энтальпия водяного пара .

По таблицам водяного пара находим 814,5 кДж/кг, r = 1973 кДж/кг,

0,1512 м³/кг. Следовательно,

814,5 + 19730,98 = 2748,5 кДж/кг.

Удельный объем влажного пара

0,15120,98 = 0,148 м³/кг.

Внутренняя энергия влажного насыщенного пара

кДж/кг.
Задача № 4.

Найти энтропию влажного насыщенного пара при р= 2,4 МПа и x = 0,8.

Решение: Из таблиц водяного пара при р= 2,4 МПа имеем 2,534 кДж/кг, 6,272 кДж/кг. Следовательно, энтропия пара

2,534+(6,272-2,534)0,8 = 5,524 кДж/(кг⁰С).
Задача № 5.

Водяной пар имеет параметры р= 3 МПа, t= 400 ⁰С. Используя таблицы водяного пара, определить значения остальных параметров.
Задача № 6.

Задано состояние пара: р= 1,6 МПа, x = 0,96. Определить, пользуясь iS – диаграммой остальные параметры и сравнить их со значениями этих же параметров, вычисленных с помощью таблиц водяного пара и соответствующих формул.

Решение: На iS –диаграмме находим точку А, характеризующую данное состояние, на пересечении изобары р₁ = 1,6 МПа и линии постоянной степени сухости х = 0,96. Проецируя ее соответственно на ось ординат и ось абсцисс, находим значение i_x= 2716 кДж/кг и S_x = 6,26 кДж/(кг⁰С).

Величина удельного объема пара определяется по значению изохоры, проходящей через точку А:

0,12 м³/кг. Для определения температуры пара нужно от точки А подняться по изобаре р= 1,6 МПа до верхней пограничной кривой (точка В). Через эту точку проходит изотерма t= 200 ⁰С; эта температура и является температурой насыщенного пара при давлении 1,6 МПа.

С
В

А
опоставим полученные значения со значениями этих же параметров, вычисленных при помощи таблиц водяного пара и соотвествующих формул. Из таблицы насыщенного водяного пара при давлении

р= 1,6 МПа находим t_н = 201,36 ⁰С; 0,1238 м³/кг; 858,3 кДж/кг; r = 1935 кДж/кг; 2,344 кДЖ/(кг⁰С); 6,422 кДЖ/(кг⁰С).

Энтальпия пара 858,3+0,961935 = 2715,9 кДж/кг;

энтропия пара 2,344+(6,422-2,344)0,96 = 6,259 кДж/кг;

удельный объем 0,1189 м³/кг.

Следовательно, совпадение значений параметров удовлетворительное.
Задача № 7.

Пользуясь диаграммой iSводяного пара, определить энтальпию пара:

а) сухого насыщенного при давлении р= 1 МПа;

б) влажного насыщенного при р= 1 МПа и х = 0,95;

в) перегретого пара при р = 1 МПа t= 300 ⁰С.
Задача № 8.

На диаграмме iSвыбрать точку в области влажного насыщенного пара и определить параметры, характеризуемые этой точкой: р, х, t, s, i.
Задача № 9.

1 кг. пара расширяется адиабатно от начальных параметров р₁ = 3 МПа и

t₁ = 300 ⁰С до р₂ = 0,05 МПа. Найти значения и работу расширения.

Решение: По диаграмме iS находим для начального состояния:

i₁ = 2988 кДж/кг; 0,081 м³/кг. Пользуясь зависимостью , получаем

кДж/кг.

Проведя на iS диаграмме адиабату до пересечения с изобарой

р₂ = 0,05 Мпа, находим i₂ = 2269 кДж/кг, х₂ = 0,837, 2,76 м³/кг,

кДж/кг.

Работа пара в процессе адиабатного расширения

2744 –2131 = 613 кДж/кг.
Задача № 10.

1 кг. пара расширяется адиабатно от начальных параметров р₁= 9 МПа и t₁=500 ⁰С до р₂= 0,004 МПа. Найти значения и работу расширения.
Тема № 9. Влажный воздух.
Задача № 1.

Определить влагосодержание воздуха при температуре t= 60 ⁰С и барометрическом давлении В = 99325 Па, если относительная влажность воздуха = 60%.

Решение: Влагосодержание воздуха . Из таблицы насыщенного водяного пара при t= 60 ⁰С , р_н = 0,0199 МПа, следовательно, парциальное давление пара в воздухе

0,6 0,0199 = 0,012 МПа.

По таблицам перегретого пара для р = 0,012 МПа и t= 60⁰С находим = 12,78 м³/кг. Тогда плотность пара

кг/м³.

Парциальное давление воздуха

99325-12000 = 0,0873 МПа.

Плотность сухого воздуха

кг/ м³.

Следовательно, влагосодержание воздуха

г/кг.
Задача № 2.

Определить абсолютную влажность воздуха, если парциальное давление пара в нем р_п = 0,014 МПа, а температура t= 60 ⁰С.
Задача № 3.

Парциальное давление пара в атмосферном воздухе 0,02 МПа, температура воздуха 70⁰С. Определить относительную влажность воздуха.
Задача № 4.

Для сушки используют воздух при t₁ = 20 ⁰С и ₁= 60%. В калорифере его подогревают до t₂ = 95 ⁰С и направляют в сушилку, откуда он выходит при t ₃= 35 ⁰С. Вычислить конечное влагосодержание воздуха, расход воздуха и теплоту на 1 кг испаренной влаги.

Решение: На диаграмме Yd находим точку К на пересечении линий t₁ = =20 ⁰С и ₁= 60% и определяем d₁ = 9 г/кг, Y₁= 40 кДж/кг. Проведя линию d= const из точки К, находим на пересечении ее с t ₂= 95 ⁰С точку L, характеризующую состояние воздуха после выхода его из калорифера. Из точки L ведем линию Y = constдо пересечения с изотермой t ₃= 35 ⁰С, где находим точку М, характеризующую состояние воздуха на выходе из сушилки. Для точки М d₃= 33 г/кг, Y₃ = 117,6 кДж/кг. Таким образом, на 1 кг сухого воздуха изменение влагосодержания составит

33-9 = 24 г/кг.

Следовательно, для испарения 1 кг влаги потребуется сухого воздуха кг. Расход теплоты в калорифере на 1 кг воздуха

117,6-40 = 77,6 кДж/кг.

Расход теплоты на 1 кг испаренной влаги (на 41,7 кг сухого воздуха) составит

q = 77,641,7= 3236 кДж/кг.