Практикум по дисциплине Архитектура и организация компьютерных систем Форма обучения очная

• Название: Практикум по дисциплине Архитектура и организация компьютерных систем Форма обучения очная
• Анкор: 123213
• Дата: 25.11.2022
• Размер: 1.85 Mb.
• Имя файла: lab aoks.doc
• Тип: Практикум; #811603
• страница: 4 из 13

Контрольный пример

Задание 1: Сложите числа:

а)10000000100₍₂₎[phone]₍₂₎=10111000110₍₂₎.

б)223,2₍₈₎+427,54₍₈₎=652,74₍₈₎.

в)3B3,6₍₁₆₎ + 38B,4₍₁₆₎ = 73E,A₍₁₆₎.

Решение:

a) 10000000100 b) 223,2 c) 3B3,6

+ 111000010 + 427,54 +38B,4

____________ ______ ______

10111000110 652,74 73E,A

Ответ:

1. 
   10111000110₍₂₎;
   
2. 
   652,74₍₈₎;
   
3. 
   73E,A₍₁₆₎.
   

Задание 2: Выполните вычитание:

а) 1100000011,011₍₂₎ - 101010111,1₍₂₎ = 110101011,111₍₂₎.

б) 1510,2₍₈₎ - 1230,54₍₈₎ = 257,44₍₈₎.

в) 27D,D8₍₁₆₎ - 191,2₍₁₆₎ = EC,B8₍₁₆₎.

Решение:

a) 1100000011,011 b) 1510,2 c) 27D,D8

- 101010111,1 - 1230,54 - 191,2

______________ ________ _______

110101011,111 257,44 EC,B8

Ответ:

1. 
   110101011,111₍₂₎
   
2. 
   257,44₍₈₎;
   
3. 
   EC,B8₍₁₆₎.
   

Задание 3: Выполните умножение:

а) 100111₍₂₎ * 1000111₍₂₎ = 101011010001₍₂₎.

б) 1170,64₍₈₎ *  46,3₍₈₎ = 57334,134₍₈₎.

в) 61,A₍₁₆₎ *   40,D₍₁₆₎ = 18B7,52₍₁₆₎.

Решение:

a) 100111 b) 1170,64 c) 61,A

*1000111 * 46,3 *40,D

__________ ________ _______

100111 355234 4F 52

+ 100111 + 732470 + 1868

100111 474320 ________

100111 __________ 18B7,52

___________ 57334,134

101011010001

Ответ:

1. 
   101011010001₍₂₎;
   
2. 
   57334,134₍₈₎;
   
3. 
   18B7,52₍₁₆₎.
   

Задания для самостоятельного выполнения

Выполните задания согласно варианту:

Вариант	Задание 1	Задание 2	Задание 3
	1111,01101(2)+11,101(2)	5774,45(8)-457,54(8)	AD(16)*51(16)
	C0D1,2(16)+A45,6(16)	10101,011(2)-1001,11(2)	4567(8)*42(8)
	78451(8)+5678,12(8)	BC,58(16)-5F,0A(16)	11110111(2)*111,011(2)
	1100,101(2)+101,11(2)	561,25(8)-17,27(8)	A12(16)*16(16)
	14C,2(16)+15,6(16)	1101,01(2)-101,1(2)	74(8)*12(8)
	154,8(8)+71,2(8)	BC,4(16)-5А,2(16)	111101(2)*11,01(2)
	1011,11(2)+11,01(2)	254,75(8)-47,67(8)	D2(16)*46(16)
	4C,8(16)+95,6(16)	110101,01(2)-11101,1(2)	77(8)*62(8)
	574,3(8)+21,56(8)	98,D(16)-3B,2(16)	110001(2)*101,01(2)
	10101(2)+1001,01(2)	125,05(8)-57,4(8)	D12(16)*16(16)
	4C,8(16)+95,6(16)	110101,01(2)-11101,1(2)	36(8)*27(8)
	264,3(8)+27,46(8)	105,D(16)-5B,2(16)	11001(2)*100,1(2)
	10011,101(2)+1001,001(2)	27,6(8)-6,12(8)	DC(16)*96(16)
	FC,8(16)+A5,6(16)	100101,01(2)-11101,1(2)	45(8)*15(8)
	54,3(8)+61,56(8)	98,D(16)-7B,9(16)	100101(2)*110,01(2)

Лабораторная работа №4 (1 часа)

Тема: Построение таблиц истинности логических функций.

Цель: Изучить стандартные логические функции.

Задание:

1. 
   Изучить основные логические функции.
   
2. 
   Изучить некоторые логические функции, производные из элементарных.
   

Теоретические сведения

Для формального описания узлов ЭВМ при их анализе и синтезе используется аппарат алгебры логики. Основные положения алгебры логики разработал в XIX в. английский математик Джордж Буль. Алгебру логики называют также булевой алгеброй.

В булевой алгебре различают двоичные переменные и переключательные функции.

Двоичные переменные могут принимать два значения: 0 и 1. Они называются также логическими или булевыми переменными и обозначаются символами х₁,x₂,х₃,...

Переключательные функции (ПФ) зависят от двоичных переменных. Они, как и аргументы, могут принимать лишь два значения: 0 или 1. ПФ называют также логическими или булевыми функциями. Будем обозначать ПФ в виде f(х₁,x₂,х₃,...). указывая в скобках аргументы, либо в виде y₁,y₂,y₃,... . ПФ в свою очередь могут служить аргументами еще более сложных логических функций. Следовательно, можно построить ПФ любой заранее заданной сложности, пользуясь ограниченным числом логических связей.

ПФ принято задавать таблицами истинности, в которых для всех наборов переменных указываются соответствующие им значения ПФ. Формирование значений ПФ в таблице истинности выполняется в соответствии с логикой работы устройства (сумматора, сдвигателя, преобразователя кодов и т. д.).

Набор переменных — это совокупность значений двоичных переменных, каждая из которых может быть равна 0 или 1. Если число аргументов (независимых переменных) ПФ равно n (т. е. х₁,x₂,х₃,...x_n), то существует 2 различных сочетаний этих переменных, т. е. наборов.

Табл. 5.1 представляет собой таблицу истинности для некоторых ПФ f₁ и f₂, зависящих от двоичных переменных х₁,x₂,х₃. Так как n = 3 (три переменных), табл. 3.1 содержит 8 строк, соответствующих 2³ = 8 наборам переменных х₁,x₂,х₃. Для каждого набора в табл. 4.1 записаны значения ПФ f₁ и f₂, равные 0 или 1. По таблице истинности записывается аналитическое выражение для ПФ (рассматривается в следующих параграфах).

Таблица 4.1

х1	х2	х3	f1	f2
0	0	0	0	1
0	0	1	1	0
0	1	0	0	1
0	1	1	1	0
1	0	0	0	0
1	0	1	1	0
1	1	0	0	1
1	1	1	0	1

Произвольная ПФ может быть выражена в форме функции от двоичных переменных (либо от других ПФ) с помощью ограниченного числа элементарных логических функций. Рассмотрим эти функции.

Логическое отрицание (функция НЕ). Логическим отрицанием переменной х называется такая ПФ f₁(x), которая имеет значение 1, когда x = 0 и значение 0, когда х= 1. ПФ НЕ обозначается в виде и читается: «f₁ есть (эквивалентно) не х».

Табл. 5.2 представляет собой таблицу истинности логической функции НЕ.

Таблица 4.2

х	f1
0	1
1	0

Функцию НЕ выполняет физический элемент (электронная схема), который называется элементом НЕ или инвертором. Обозначение инвертора на функциональных схемах показано на рис. 4.1.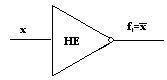



Рис. 4.1.
Логическое умножение (конъюнкция). Конъюнкция двух (или любого другого числа) переменных х₁ и х₂ принимает значение 1 только на наборе, в котором все переменные имеют значения 1. На остальных наборах эта функция имеет значение 0.

Таблица 4.3

x1	x2	f2
0	0	0
0	1	0
1	0	0
1	1	1

Табл. 4.3 представляет собой таблицу истинности конъюнкции двух переменных х₁ и x₂. ПФ конъюнкция обозначается в виде 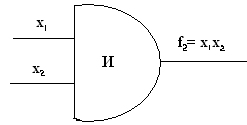и читается: «f₂ есть (эквивалентно) х₁ и x₂».



Рис. 4.2.
Для обозначения конъюнкции можно использовать символы или &. Конъюнкция называется также функцией И, так как она имеет значение 1, только если первый и второй аргументы имеют значения 1.

Функция И выполняется электронной схемой, которая называется элементом И или коньюнктором. Обозначение элемента И на функциональных схемах показано на рис. 4.2. Число входов элемента И равно числу переменных, участвующих в операции умножения.

Логическое сложение (дизъюнкция). Дизъюнкция двух (или любого другого числа) переменных х₁ и х₂ имеет значение 0 только на наборе, в котором все переменные имеют значение 0. Если хотя бы одна из переменных равна 1, функция будет иметь значение 1.

Табл. 4.4 есть таблица истинности для дизъюнкции двух переменных х₁ и х₂. ПФ дизъюнкция записывается в виде и читается: «f₃ есть (эквивалентно) х₁ или x₂». Кроме символа + , для дизъюнкции употребляется символ V.

Так как функция дизъюнкции имеет значение 1, если первый или второй аргументы имеют значение 1, операция дизъюнкции называется также операцией ИЛИ.

Таблица 4.4

x1	x2	f3
0	0	0
0	1	1
1	0	1
1	1	1

Операция ИЛИ реализуется электронной схемой, которая называется элементом ИЛИ или дизъюнктором. Обозначение элемента ИЛИ на функциональных схемах показано на рис. 4.3. Число входов элемента ИЛИ равно числу переменных, участвующих в операции дизъюнкции.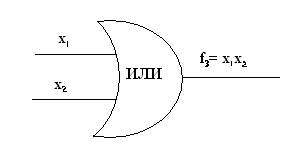



Рис.4.3.

Элементарные логические функции НЕ, И, ИЛИ являются основными логическими функциями. Имеется еще несколько логических функций, производных от основных функций (т. е. выражающихся через функции НЕ, И, ИЛИ), которые реализуются соответствующими электронными элементами и так часто встречаются в схемотехнике ЭВМ, что им были даны собственные названия. Рассмотрим эти функции.

Отрицание конъюнкции (операция И — НЕ). Эта функция образуется путем отрицания результата, получаемого при выполнении операции И. Табл. 4.5 есть таблица истинности операции И — НЕ для двух переменных. Из сравнения табл. 4.3 и 4.5 видно, что ПФ И — НЕ является отрицанием (операцией НЕ) конъюнкции. ПФ И — НЕ записывается в виде

Таблица 4.5.

x1	x2	f4
0	0	1
0	1	1
1	0	1
1	1	0

Функцию И — НЕ выполняет схема, которая называется элементом И — НЕ. Обозначение элемента И — НЕ на функциональных схемах показано на рис. 4.4. Число входов элемента И — НЕ определяется числом аргументов функции И — НЕ.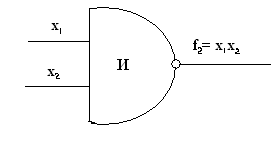



Рис. 4.4.

Отрицание дизъюнкции (операция ИЛИ — НЕ). Эта операция образуется путем отрицания результата, полученного при выполнении операции ИЛИ. Табл. 4.6 представляет собой таблицу истинности операции ИЛИ — НЕ для двух переменных. Из сравнения табл. 4.4 и 4.6 видно, что ПФ ИЛИ — НЕ является отрицанием (операцией НЕ) дизъюнкции. ПФ ИЛИ — НЕ записывается в виде

Таблица 4.6.

x1	x2	f5
0	0	1
0	1	1
1	0	1
1	1	0

Операцию ИЛИ — НЕ выполняет электронный элемент, который называется элементом ИЛИ — НЕ. Обозначение элемента ИЛИ — НЕ на функциональных схемах показано на рис. 4.5. Число входов элемента ИЛИ — НЕ определяется числом аргументов функции ИЛИ — НЕ.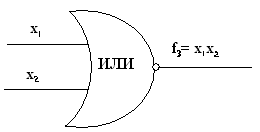



Рис.4.5.

ИСКЛЮЧАЮЩЕЕ ИЛИ (операция НЕРАВНОЗНАЧНОСТЬ или СЛОЖЕНИЕ ПО МОДУЛЮ ДВА). Данная функция имеет значение 1 на тех наборах переменных, в которых число единиц нечетно. Для двух переменных операция НЕРАВНОЗНАЧНОСТЬ иллюстрируется таблицей истинности (табл. 4.7). Эта операция записывается для двух переменных в виде /

Условное обозначение элемента, выполняющего функцию НЕРАВНОЗНАЧНОСТЬ, на функциональных схемах приведено на рис. 4.6. Символ 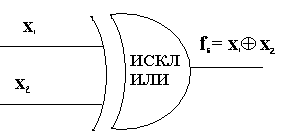в поле элемента означает «сложение по модулю два».



Рис.4.6.

Операция НЕРАВНОЗНАЧНОСТЬ выражается через операции НЕ, И, ИЛИ в виде .

Таблица 4.7.

x1	x2	f6
0	0	0
0	1	1
1	0	1
1	1	0

Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ (РАВНОЗНАЧНОСТЬ). Функция РАВНОЗНАЧНОСТЬпредставляет собой отрицание операции ИСКЛЮЧАЮЩЕЕ ИЛИ.

Данная операция имеет значение 1 на тех наборах переменных, которые содержат четное число единиц. Для двух переменных операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ представлена таблицей истинности (табл. 4.8). Эта операция записывается для двух переменных в виде

Таблица 4.8.

x1	x2	f6
0	0	1
0	1	0
1	0	0
1	1	1

Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ выражается через операции НЕ, И, ИЛИ в виде .

Функцию РАВНОЗНАЧНОСТЬ выполняет электронный элемент с аналогичным названием, изображение которого на функциональных схемах дано на рис. 4.7.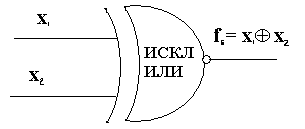



Рис. 4.7.
Контрольный пример

Задание: Даны двоичных числа А=0110 и В=0101. Выполнить операции:

1. 
   отрицание
   
2. 
   логическое сложение
   
3. 
   отрицание ИЛИ
   
4. 
   логическое умножение
   
5. 
   отрицание И
   
6. 
   исключающее ИЛИ
   
7. 
   отрицание исключающего ИЛИ
   

Решение:

1. 
   
   
2. 
   А+В = 0111
   
3. 
   
   
4. 
   АВ=0100
   
5. 
   
   
6. 
   
   
7. 
   
   

Задания для самостоятельного выполнения

Даны двоичных числа А и В (данные в таблице). Выполнить операции:

1. 
   отрицание
   
2. 
   логическое сложение
   
3. 
   отрицание ИЛИ
   
4. 
   логическое умножение
   
5. 
   отрицание И
   
6. 
   исключающее ИЛИ
   
7. 
   отрицание исключающего ИЛИ
   

Вариант	А	В
	0110	0110
	0001	1001
	1001	0010
	1010	1100
	1011	1101
	1001	0111
	1011	0011
	1001	1111
	0001	1010
	1101	1110
	1111	0101
	1011	0110
	1010	1011
	1010	1101
	1101	1011

Лабораторная работа №5 (1 часа)