ТВН лаб.ур.. Практикум по дисциплине Техника высоких напряжений

• Название: Практикум по дисциплине Техника высоких напряжений
• Анкор: ТВН лаб.ур
• Дата: 17.11.2022
• Размер: 4.03 Mb.
• Имя файла: b817085.doc
• Тип: Практикум; #792878
• страница: 4 из 9

Таблица 3.1

№ п/п	U1, В	U2, кВ U2=kгрU1	U2i, кВ	№ п/п	U1, В	U2, кВ	U2i, кВ
1				26
2 … 25				27 … 50

Таблица 3.2

№ п/п

По полученным и рассчитанным данным построить гистограммы для p_k(ΔU_k) и P_i(U_p U_i), интегральную кривую нормального распределения Гаусса в пределах ( )…( ).

Вероятность попадания нормально распределенной случайной величины U (в нашем случае - вероятность пробоя) в интервал (U₁, U₂) вычисляется по формуле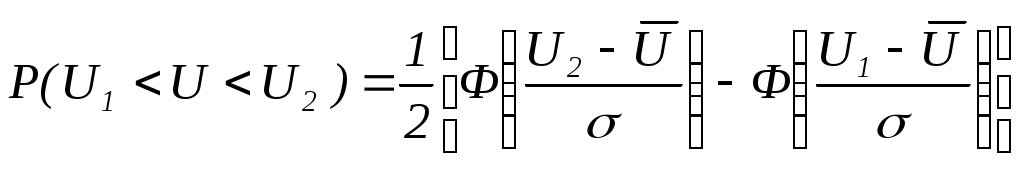

,

где 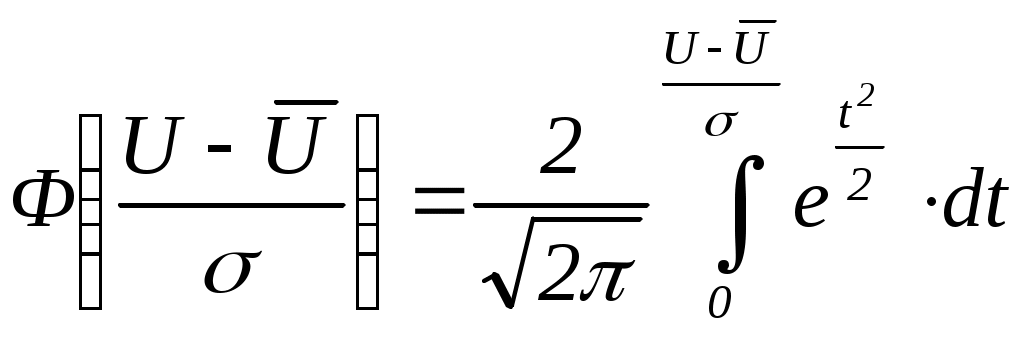- функция Лапласа (интеграл вероятности), некоторые значения которой приведены в таблице.

Таблица 3.3

	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
0	0	0,0797	0,1585	0,2358	0,3108	0,3829	0,4515	0,5161	0,5763	0,6319
1	0,6827	0,7287	0,7699	0,8064	0,8385	0,8664	0,8904	0,6109	0,9231	0,9426
2	0,9545	0,9643	0,9786	0,9876	0,9836	0,9876	0,9907	0,9931	0,9949	0,9963
3	0,9973	0,9981	0,9986	0,9990	0,9993	0,9995	0,9997	0,9998	0,9998	0,9999

Приведем расчет одной точки. Допустим, по экспериментальным данным =5 кВ, 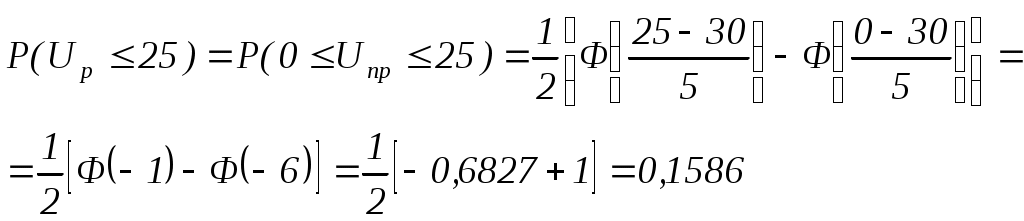=30 кВ. Определим .



Интеграл вероятности является функцией нечетной и

.

Аналогично рассчитываются все остальные точки в пределах от - 3σ – до

+3σ.
3.4. Содержание отчета

1. 
   Цель работы и методика ее проведения.
   
2. 
   Схема испытательной установки и параметров основного оборудования
   
3. 
   Результаты испытаний и расчетов в виде таблиц и графиков.
   
4. 
   Расчетные формулы и примеры расчета основных величин ( , σ, ).
   
5. 
   Основные результаты, полученные по программе ЭВМ.
   
6. 
   Выводы по работе.
   

3.5. Контрольные вопросы

1. 
   Чем определяется разброс пробивных напряжений образцов изоляции?
   
2. 
   Почему разброс пробивных напряжений жидкой изоляции больше, чем воздушной?
   
3. 
   Является ли исчерпывающей характеристикой изоляционных возможностей конструкции величина ?
   
4. 
   Поясните смысл основных параметров нормального распределения (σ, ).
   
5. 
   Почему нормальное распределение Гаусса удовлетворительно аппроксимирует экспериментальную кривую P (U_p = U_i) в пределах ?
   
6. 
   Часто очень важной величиной для оценки изоляции является величина U_p,min. Почему?
   
7. 
   Определите необходимый объем испытаний для оценки и σ при заданной величине погрешности.
   

Литература: [1], с.41-43; [3], с.78-81;

[6], справочники и пособия по теории вероятности и математической статистике.

Лабораторная работа № 4