Практикум по курсу Экономикоматематические модели и методы
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Лабораторный практикум по курсу «Экономико-математические модели и методы» Лабораторная работа №1 «Модель межотраслевого баланса» Подготовила А.А. Коробецкая Работа посвящена изучению модели межотраслевого баланса (МОБ) и расчетам по ней средствами MS Excel 2007. Лабораторная работа содержит три задания: Выполнение расчетов с матрицами в MS Excel 2007. Нормативный расчет межотраслевого баланса. Статистический расчет межотраслевого баланса. Рассматривается инструмент «Поиск решения». Каждое задание оформляется на отдельном листе в общей книге Excel. На каждом листе указывается номер и название задания, ФИО и группа выполнившего, номер варианта. Отчет по работе выполнять не требуется, к сдаче предоставляется только файл Excel. СодержаниеЗадание 1.Операции с матрицами 5 Подготовка к работе. Поиск решения«Поиск решения» – это инструмент, позволяющий подбирать значения ячеек, так чтобы найти минимум, максимум или определенное значение. Кнопка «Поиск решения» находится на вкладке «Данные»:  По умолчанию «Поиск решения» в Excel отключен и кнопка не отображается. Чтобы включить его, необходимо выполнить следующую последовательность действий. В меню Office нажать кнопку «Параметры Excel»  В окне параметров Excel выбрать «Надстройки», выделить пункт «Пакет анализа» и нажать кнопку «Перейти...»  В окне «Надстройки» поставить галочку «Поиск решения» и нажать «OK»  После нажатия на кнопку «Поиск решения» появляется окно:  Таким образом, для поиска решения необходимо задать: целевую ячейку – ячейка с формулой, для которой ищется максимум, минимум или корень; изменяемые ячейки – одна или несколько ячеек с управляемыми переменными; их значения входят в формулу целевой ячейки; ограничения (необязательно) – диапазоны изменения переменных, условия на значений и др. Введенные параметры сохраняются для каждого листа, так что при повторном поиске решения вводить их заново не потребуется. Пример Найти минимум функции: f(x) = 10 – 2x + 0,5x4 Для решения потребуется как минимум две ячейки: в одну будет помещено решение (значение x), в другую – сама функция, которую нужно минимизировать. 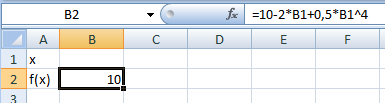 Поиск решения: целевая ячейка – ячейка с формулой для f(x), «изменяя ячейки» – ячейка для x, ограничений нет.  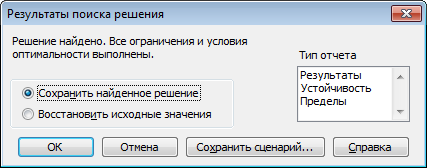 Результат: 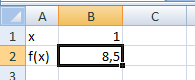 Операции с матрицамиЗаданиеЗаданы матрицы A и B, вектор C и константы a, b. Вычислить: определители матриц  ; ;транспонированные матрицы 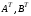 ; ;обратные матрицы 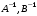 ; ;произведение матриц  ; ;значение 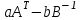 . .Решить систему уравнений вида 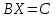 , где , где 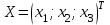 – вектор переменных. Решение найти двумя способами: – вектор переменных. Решение найти двумя способами: с помощью матричных операций; с помощью «Поиска решений». Пример варианта задания
Указания к выполнениюДля выполнения операций с матрицами в Excel присутствует несколько функций и специальный режим редактирования, когда несколько ячеек представляют собой одно целое (матрицу или вектор). Создайте и сохраните новую книгу Excel. Переименуйте «Лист 1» в «Задание 1». Добавьте на лист «Задание 1» шапку (см. скриншот). Введите исходные данные и настройте форматирование ячеек. Матрицы и вектор записываются в виде таблиц. 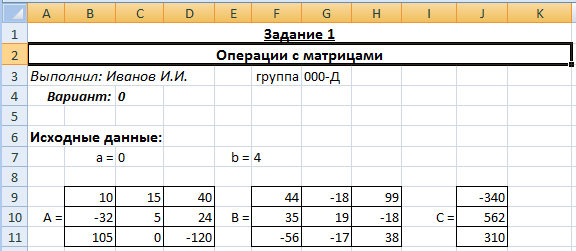 Обратите внимание: числа и подписи к ним находятся в разных ячейках, иначе значения нельзя будет использовать в расчетах. Для аккуратного оформления установите выравнивание числа по левому краю, а подписи – по правому. Выполнение расчетов. Для расчета определителя в Excel используется формула МОПРЕД(массив). Это обычная формула, результатом является число. 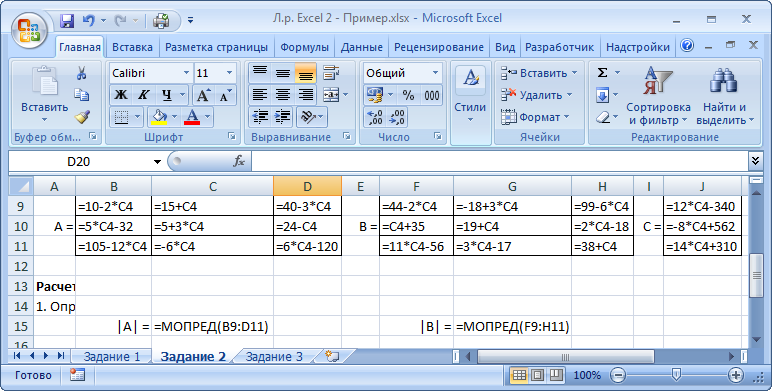  Транспонирование матрицы выполняется с помощью функции ТРАНСП(диапазон), но результатом в данном случае будет не одно число, а тоже матрица, т.е. несколько ячеек одновременно. В Excel существует способ для ввода общей формулы для диапазона ячеек. Для этого: выделите диапазон ячеек, в которых будет размещен результат (B17:D19); нажмите F2 на клавиатуре – Excel перейдет в режим ввода формулы; введите =ТРАНСП(B10:D11), но не выходите из ячейки; нажмите Ctrl+Shift+Enter. В результате формула будет распространена (не растянута!) на весь диапазон B17:D19. Теперь редактировать его можно только целиком, используя сочетание клавиш Ctrl+Shift+Enter. Формула при этом отображается в фигурных скобках. 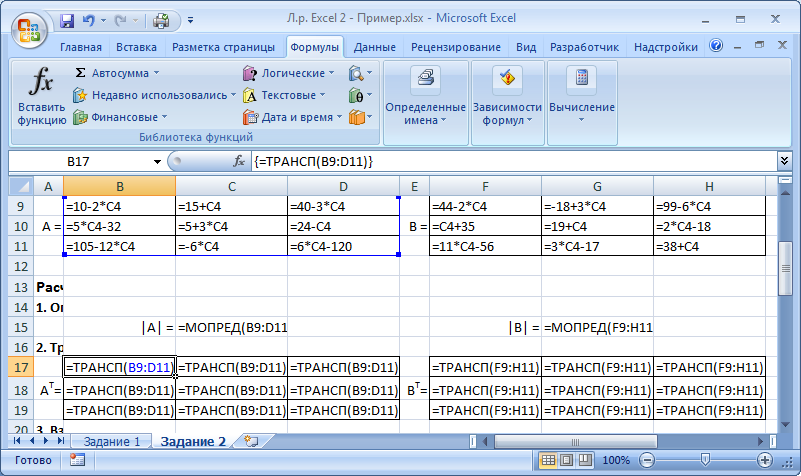  Чтобы оформить верхний или нижний индексы (в данном случае T), во время набора текста выделите только нужный символ, правый клик – «Формат ячеек...», вкладка «Шрифт», поставить галочку «надстрочный» или «подстрочный». Формулы для следующих расчетов: МОБР(диапазон) – обратная матрица; МУМНОЖ(диапазон1;диапазон2) – умножение двух матриц. Они также вводятся как формулы диапазона.  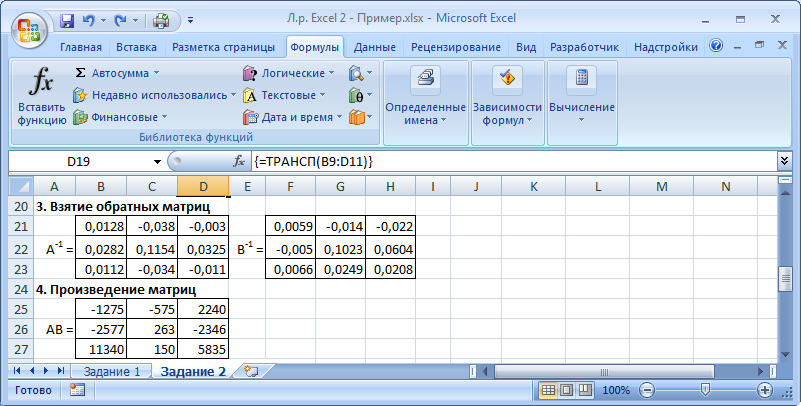 Арифметические действия с матрицами можно выполнять двумя способами: а) с отдельными ячейками (поэлементно); б) целиком для матриц, используя формулы для диапазона.   Решение системы уравнений в матричном виде. Из курса линейной алгебры известно, что решение уравнения вида 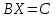 можно найти как 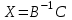 . .Таким образом, достаточно взять обратную матрицу 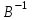 и умножить ее на вектор С. и умножить ее на вектор С.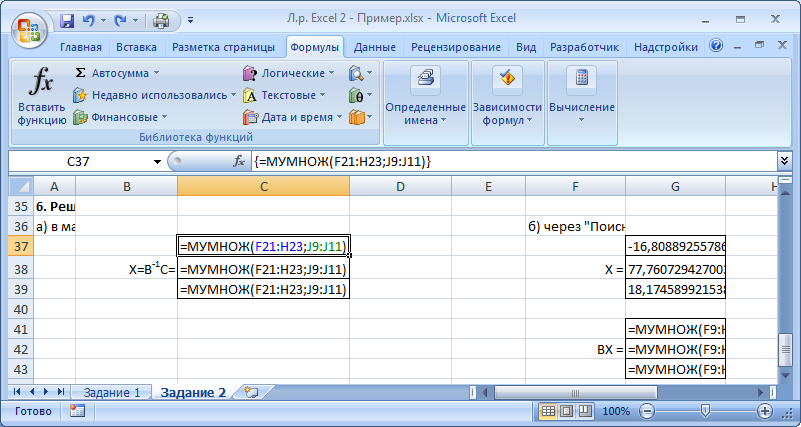 Для использования «Поиска решения» необходимо задать целевую функцию. В данном случае можно записать: 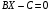 . .Введем эту формулу и подготовим место для значений X. 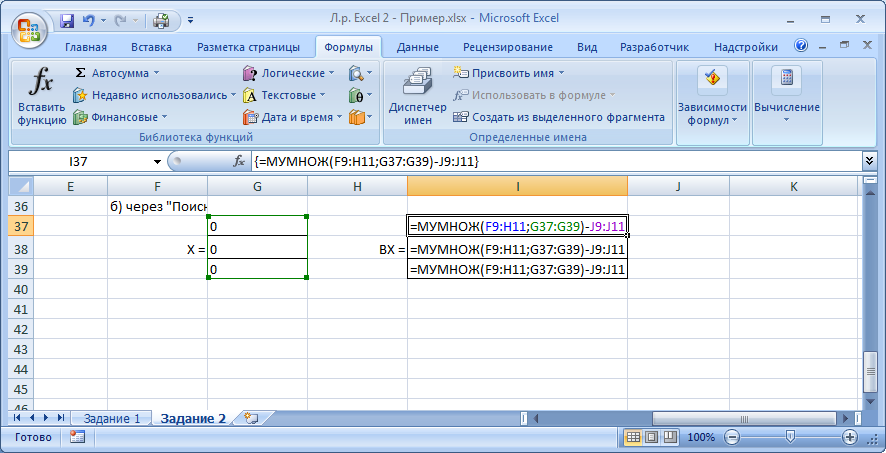 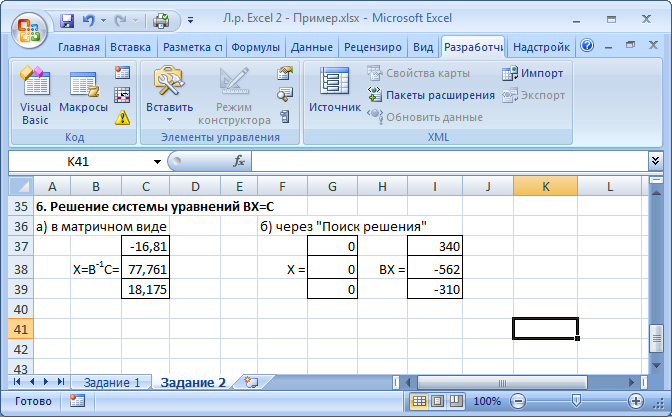 Значения ячеек I37:I39 необходимо установить равными нулю. Но в «Поиске решения» в качестве целевой функции можно задать только одну ячейку. Поэтому I37 мы будем использовать как целевую функцию, а для I38 и I39 зададим ограничения: 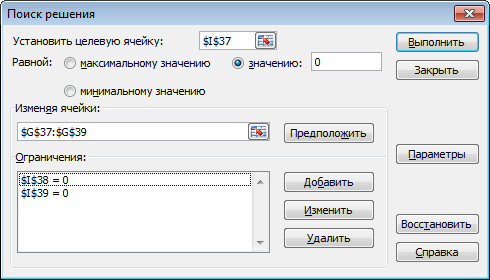 В результате получим: 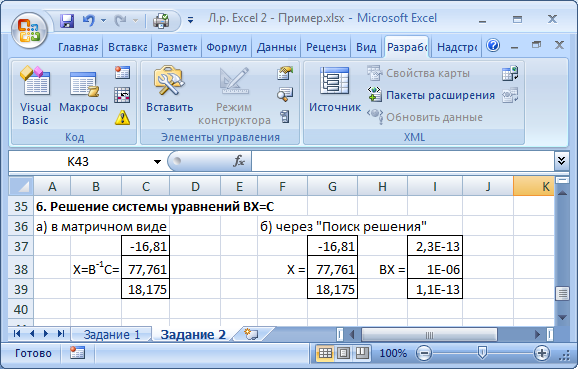 Таким образом, оба метода дают одинаковый результат. Замечание: Вектор BX после поиска решений содержит очень малые, близкие к 0 значения (2E-13 = 2∙10-13 и т.д.). Это отличие от нуля возникает из-за ошибки округления. Задание 2. Нормативный расчет МОБЗаданиеЗаданы матрица коэффициентов прямых затрат A и вектор конечного потребления Y. Вычислить матрицу коэффициентов полных затрат B. Проверить продуктивность матрицы A. Заполнить таблицу МОБ: Вычислить вектор валового продукта X. Рассчитать объемы межотраслевых поставок продукции xij. Вычислить добавленную стоимость Z. Пример варианта задания
Указания к выполнениюПерейдите на «Лист 2» и переименуйте его в «Задание 2». Скопируйте вариант задания, заполните «шапку». 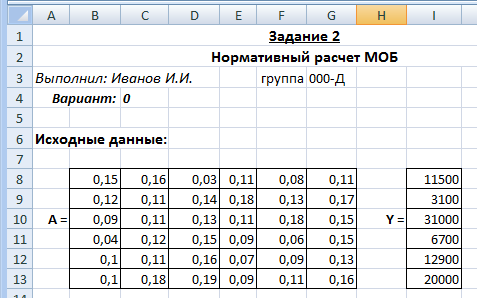 Вычислим матрицу коэффициентов полных затрат по формуле:  Для этого сначала необходимо вычислить матрицу  , где E – единичная матрица. , где E – единичная матрица.Для заполнения E удобнее сначала ввести везде 0 с помощью «растягивания», а затем уже вписать 1 по диагонали. 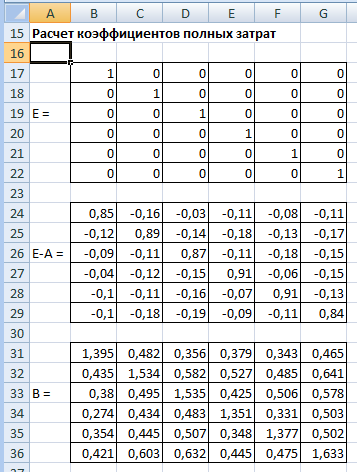 2. Все значения матрицы B положительные, следовательно, матрица A продуктивна и обеспечивает положительную величину конечного производства по всем отраслям. На диагонали матрицы B значения > 1, а остальные ячейки меньше 1. 3. Расчертим место для таблицы межотраслевого баланса (раскрашивать необязательно): 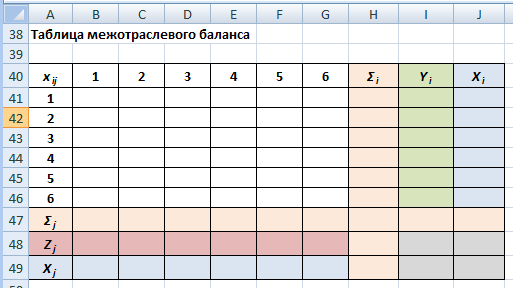 Чтобы вставить значок суммы, нажмите на ленте на вкладке «Вставка» кнопку «Символ» 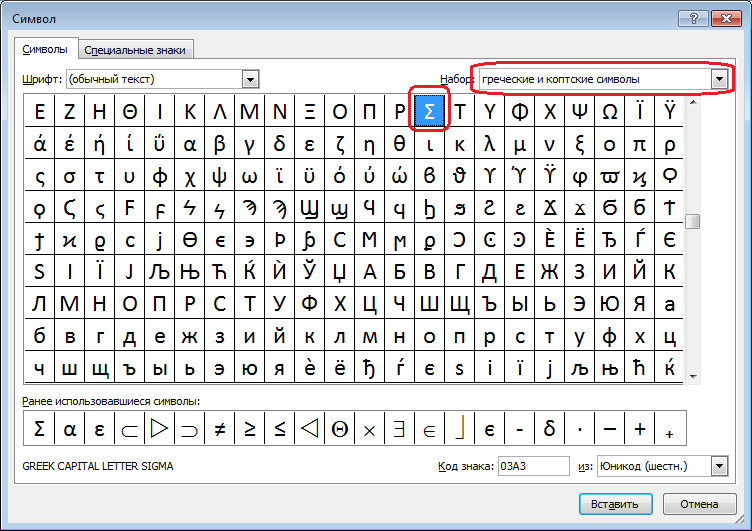 Порядок заполнения таблицы: Скопировать значения конечного потребления Yi из исходных данных.  Вычислить столбец валового продукта Xi по формуле: X = (E – A)–1 Y Заполнить строку Xj путем транспонирования столбца Xi. Рассчитать объемы межотраслевых поставок продукции по формуле: xij = aij Xj Чтобы было удобно растягивать формулы, зафиксируйте в формуле Excel только номер строки для Xj (два раза нажать F4 или вручную вписать $): =B8*B$49 Вычислить итоги Σi и Σj как суммы соответствующих строк и столбцов. Вычислить добавочную стоимость Zj по формуле: Zj = Xj – Σj 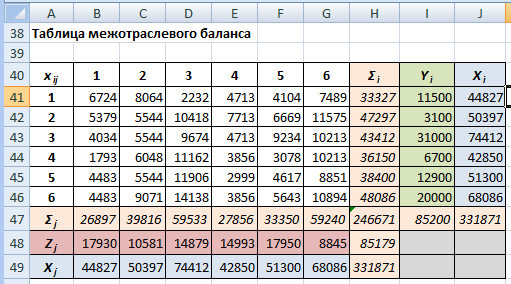 Проверьте себя! Σi + Yi = Xi Σ Zj= Σ Yi Σ Xj= Σ Xi Небольшие расхождения (как и в примере) возможны из-за ошибок округления. Задание 3. Статистический расчет МОБЗаданиеНародное хозяйство некоторой страны было разбито на пять основных отраслей: Тяжелая промышленность. Легкая промышленность. Строительство. Сельское хозяйство. Транспорт. Статистические данные содержат следующие сведения (в млн. д.е.): межотраслевой баланс за прошлый год; оплата труда по отраслям; суммарная амортизация по отраслям; валовой продукт по отраслям. Вычислить коэффициенты прямых затрат. Какие отрасли какой продукции потребляют больше всего? меньше всего? Вычислить коэффициенты полных затрат. Проверить продуктивность экономики. Сколько всего продукции должна произвести каждая отрасль для производства конечной продукции на 1 млн. д.е.? Определить добавочную стоимость и валовую прибыль по отраслям. Есть ли среди отраслей убыточные? Рассчитать суммарные объемы промежуточного и конечного потребления. Чему равен ВВП страны? Какая отрасль занимает первое место по производству конечной продукции? по общему объему производства? Пример варианта задания
Указания к выполнениюПерейдите на «Лист 3», переименуйте его в «Задание 3». Заполните «шапку» и вставьте исходные данные.  Добавьте в таблицу межотраслевого баланса недостающие строки и столбцы. Под таблицей выделите место для матрицы коэффициентов прямого и полного потребления. 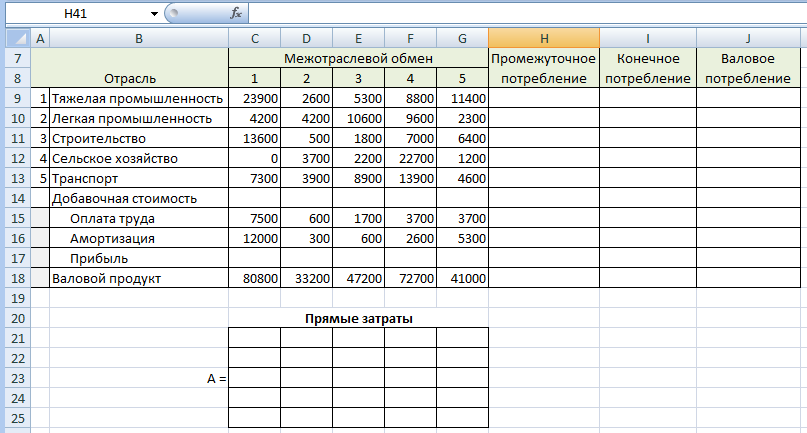 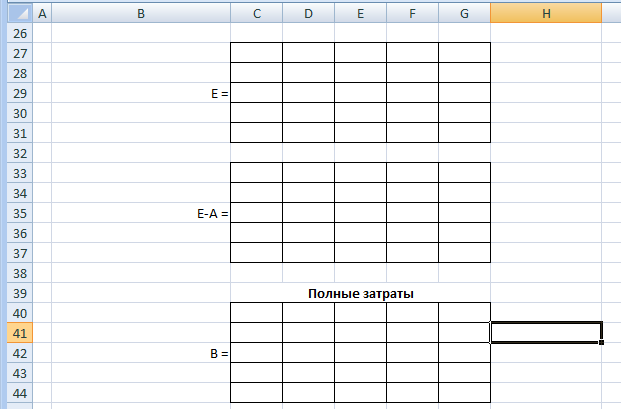 Вычислим коэффициенты прямых затрат по формуле: aij = xij / Xj 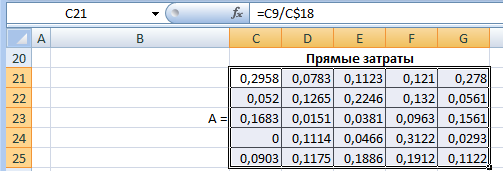 Вывод: Тяжелая промышленность больше всего потребляет собственной продукции (a11 = 0,296), и не потребляет продукцию сельского хозяйства (a41 = 0). Легкая промышленность также больше всего потребляет собственной продукции, но не намного больше, чем продукцию сельского хозяйства и транспорта (a22 = 0,127, a42 = 0,111, a52 = 0,118). Строительство в легкой промышленности почти не ведется (a32 = 0,015). В строительстве больше всего используется продукции легкой промышленности (a23 = 0,22), а меньше всего – собственной и сельского хозяйства (a33 = 0,38, a43 = 0,047). В сельском хозяйстве больше всего потребляется собственной продукции (a44 = 0,312), меньше всего – строительной (a25 = 0,056). Транспортная отрасль больше всего потребляет продукции тяжелой промышленности (a15 = 0,278), меньше всего – легкой (a25 = 0,029). Вычислим матрицу полных затрат по аналогии с заданием 2: 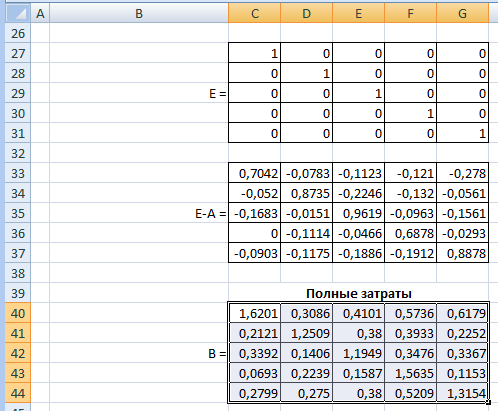 Вывод Все коэффициенты полных затрат положительны, следовательно экономика продуктивна (конечный продукт по всем отраслям положителен). Для выпуска 1 млн. д.е. конечной продукции тяжелой промышленности требуется произвести продукции на сумму 1,62 млн.д.е. Для легкой промышленности – на сумму 1,25 млн.д.е. Для строительства – на сумму 1,19 млн.д.е. Для сельского хозяйства – на сумму 1,56 млн.д.е. Для транспорта – на сумму 1,31 млн.д.е. Вычислим валовую прибыль P по отраслям, как разницу между валовым выпуском и всеми видами затрат (A – амортизация, L – оплата труда): Pj = Xj – Σj – Aj – Lj  Добавочную стоимость Z можно вычислить по любой из двух формул: Zj = Xj – Σj или Zj = Lj + Aj +Pj  Вывод Прибыль во всех отраслях положительная, убыточных отраслей нет. Наименьшую прибыль дает сельское хозяйство, наибольшую – легкая промышленность. При этом валовой продукт сельского хозяйства более чем в 2 раза превышает значение легкой промышленности. Но и затраты на производство в легкой промышленности значительно ниже по всем строкам. Вычислим суммарные объемы промежуточного и конечного потребления. Сначала транспонируем строку с валовым производством, чтобы получить валовое потребление. Промежуточное потребление равно сумме потребления по строкам. Конечное потребление равно разнице между валовым и промежуточным потреблением. Также добавим строку с итоговыми (суммарными) показателями. Окончательно матрица межотраслевого баланса примет вид:  Вывод ВВП страны равен 94 300 млн. д.е. Наибольший объем конечного потребления принадлежит сельскому хозяйству (45% ВВП), наименьший – легкой промышленности и транспорту (по 2,5% ВВП). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
