Методичка Excel. Практикум по курсу Информатика
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
Задание 1. Обработка данных
А2 – исходные значение, x В2 – удвоенное значение, 2*x С2 – квадрат значения, x2 D2 – cos2(х) -1
соответственно.
Проверьте правильность вычислений. Если результаты неверны, найдите и исправьте ошибку!
Сохраните свою работу под именем Занятие2. Задание 2. Построение графиковЛист1. Путем подбора параметров найдите корень уравнения cos(x)-x=0 с погрешностью < 0,001 Лист2. Постройте график функции y= cos2 (x)-1. Лист3. Постройте в одной системе координат графики следующих двух функций y=2sin(x); y=3cos(2x)-sin(x) для x, принадлежащему [-3; 0]. Лист4. Постройте поверхность для следующей функции z=x2-y 2 при x принадлежащему [-2; 2], hx=0,2 y принадлежащему [-1; 1], hy=0,2 Сохраните свою работу под именем Занятие4. Занятие 5. Финансовый анализ в MS EXCEL
Многие функции имеют одинаковые аргументы. Представим их в таблице:
Рассмотрим финансовые функции, связанные с интервалом выплат. Интервал выплат – это последовательность постоянных денежных платежей, делаемых в непрерывный период. В функциях, связанных с интервалами выплат, выплачиваемые деньги представляются отрицательным числом, получаемые деньги - положительным числом. Функция ПС Синтаксис: =ПС(ставка; кпер; плт; бс; тип) Функция ПС является наиболее распространенным способом оценки привлекательности долговременных вложений. Текущее значение вложения (чистый текущий объем вклада) определяется дисконтированием (приведением к стоимости на настоящий момент) поступлений по этому вложению. Если текущая стоимость поступлений оказывается больше вклада, вложение считается удачным. Функция ПС вычисляет текущую стоимость ряда равных по величине периодических выплат или единовременной выплаты (периодические выплаты постоянной величины называют обыкновенной рентой). Для вычисления текущей стоимости ряда выплат используется аргумент выплата, а для вычисления текущей стоимости единовременной выплаты – аргумент бс .Для вложения с рядом периодических выплат и единовременной выплатой используются оба этих аргумента. Задача 1. Существует возможность вложения, которое ежегодно возвращает 1000р. в течение следующих пяти лет. Но для этого нужно вложить 4000р. Имеет ли смысл вкладывать 4000р. сегодня, чтобы заработать 5000р. в течение последующих 5 лет? Для определения текущей стоимости этого вложения используется формула =ПС(4,5%; 5; 1000). В этой формуле используется аргумент выплата и не задействован аргумент бс. Аргумент выплата равен 1000 (положительное число), поскольку деньги получают, а не отдают. Формула возвращает результат −4389,98. Это означает что нужно 4389,98р. вложить (отдать, поэтому результат функции -отрицательное число) в банк под 4,5% годовых сегодня , чтобы получить 5000р. в течение следующих 5 лет. Поскольку в предлагаемой сделке вложение составляет 4000р., можно считать предложение выгодным. Примечание. Если тип=0 и бс=0, то значение функции ПС вычисляется по формуле А Здесь А – плт, i –ставка, n- кпер. Задача 2 . Вас просят дать в долг 10000р. и обещают возвращать по 2000р. в течение 6 лет. Будет ли эта сделка выгодна при годовой ставке банка 7%? Решение задачи удобно оформить в виде таблицы: 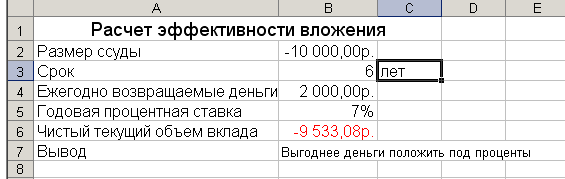 Рис.1 В ячейке В6 записана формула для вычисления текущей стоимости вложения: =ПС (В5; В3; В4). Для автоматизации составления таблицы и получения ответа на вопрос, выгодна ли сделка, в ячейки таблицы введены следующие формулы: Ячейка Формула С3 =ЕСЛИ (В3=1;"год";ЕСЛИ(В3<=4;"года";"лет")) В7 =ЕСЛИ(ABS(B2) Функция АВS(x) вычисляет |x|. Как видно из рис. 1, в рассмотренном случае деньги выгоднее положить под проценты. Задача 3. Можно вложить 4000р. и получить по истечении 5лет 5000р.(в конце срока). Есть возможность положить деньги в банк под 4,5% годовых. Необходимо оценить выгодность предложения. Для решения задачи потребуется формула: =ПС(4,5%; 5; ; 5000). Здесь используется аргумент бс и не используется аргумент плт. Эта формула возвращает значение −4012,26. Это означает, что 5000р., которые вкладчик получит через 5 лет, сегодня стоят 4012,26 р. при ставке 4,5%. По условиям сделки нужно вложить 4000 р. (то есть меньше, чем 4012,26 р.), значит предложение является выгодным. Задача 4. Сделка рассчитана на 5 лет. Если вложить 4000 р., ежегодно будет возвращаться 500р., кроме того, в конце срока будет выплачено 3000 р. Можно положить деньги на краткосрочный вклад под 4,5%. Определить выгодно ли вложение. Решить задачу можно с помощью формулы: =ПС(4,5%; 5; 500; 3000) В этой формуле одновременно используются и аргумент плт и аргумент бс. Результатом функции является значение −4602,32. Это означает, что надо вложить в банк 4602,32р. чтобы получить тот же результат. Поскольку значение 4602,32 больше 4000, предложение является выгодным. Функция ЧПС Синтаксис: =ЧПС ( ставка; значение1; значение2;…). Функция ЧПС также вычисляет величину чистой приведенной стоимости инвестиции и может быть использована для определения выгодности вложения. Чистая текущая стоимость (чистый текущий объем вклада) – это сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения). Функция ЧПС отличается от ПС двумя аспектами:
Задача 5 Предложена сделка, согласно которой можно вложить 10000р. и по истечении года получить 2000р., через год еще 4000, и еще через год 7000р. Есть альтернатива положить деньги в банк под 10% годовых. Оценить выгодность сделки. Для решения задачи потребуется формула: =ЧПС(10%; 2000; 4000; 7000). Результат, равный 10383,17р., говорит о том, что можно рассчитывать на получение чистой прибыли от этого вложения: в банк пришлось бы вложить большую сумму, чтобы получить ту же прибыль, что и в предлагаемой сделке. Задача 6 Какую сумму надо положить в банк под 4,5% годовых, чтобы через год получить 1000 р. Ответ можно получить с помощью формулы =ЧПС(4,5%; 1000). Функция дает результат равный 956,94. Если n – это количество денежных взносов в списке значений, Pj – j-oe значение и i-ая ставка, то возвращаемое значение функцией ЧПС вычисляется по формуле 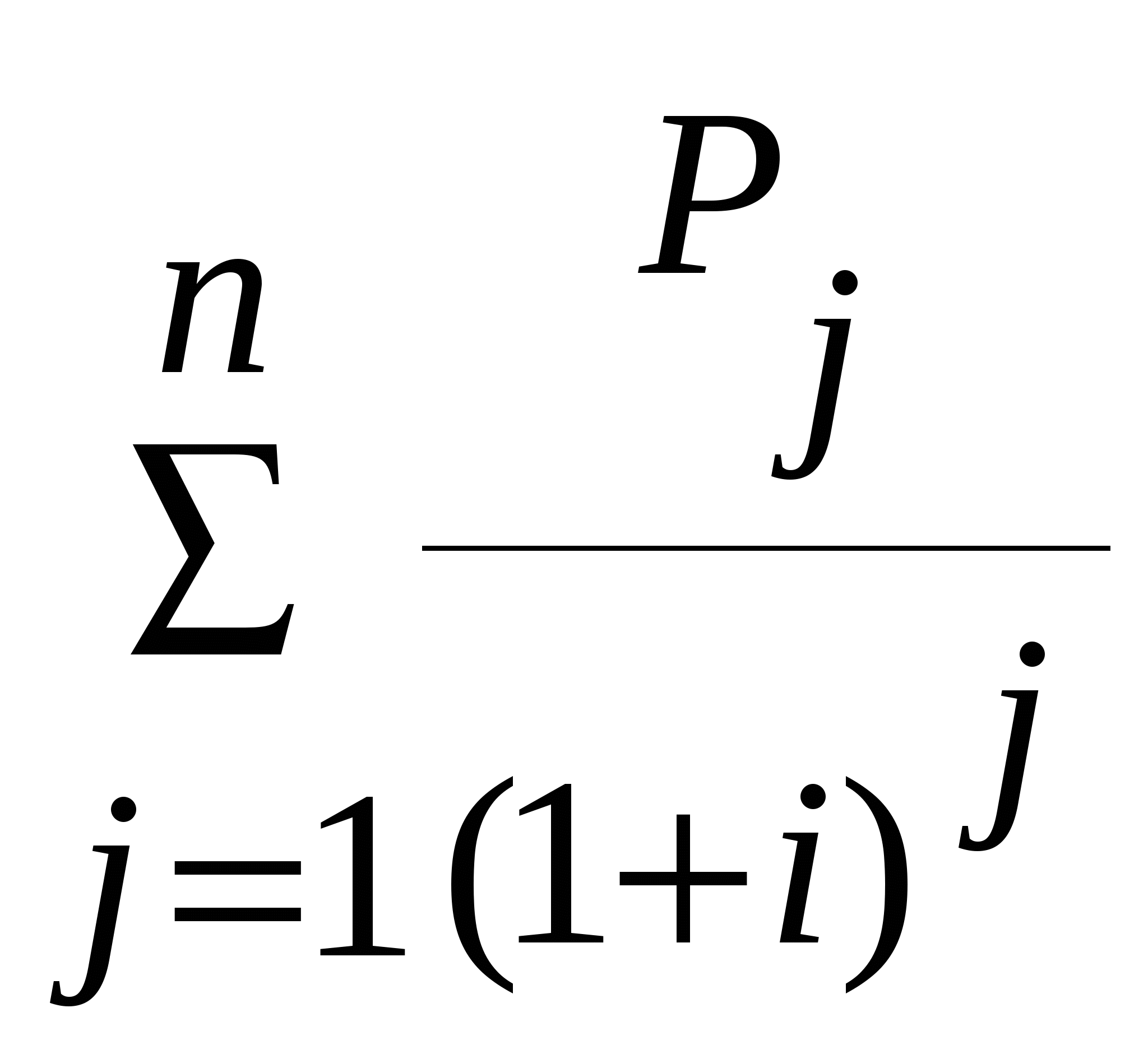 . .Функция БС Функция БС – вычисляет будущую стоимость вклада на основе периодических постоянных (равных по величине) платежей и постоянной процентной ставки. Функция БС подходит для расчета итогов накоплений при ежемесячных банковских взносах. Синтаксис: =БС(ставка; кпер; плт; пс;тип). Здесь ставка - процентная ставка за период; кпер - число периодов; плт - величина постоянных периодических платежей; пс - текущее значение, т.е. общая сумма, которую составляют будущие платежи. Приведенная (нынешняя) стоимость, или общая сумма, которая на настоящий момент равноценна серии будущих выплат (пс=0). тип - (0 или1). Если оплата производится в конце периода, то тип=0 (или значение опущено), если в начале периода - тип=1. Если тип=0 и пс=0, то БС вычисляется по формуле где А - плт; i – ставка; n – число периодов. Задача 7 Вкладчик открывает счет и планирует вносить на счет 2000 рублей в начале каждого месяца и рассчитывает на среднюю скорость оборота 11% в год на протяжении всего срока. Какая сумма будет на счете через 5 лет? Для решения задачи потребуется формула: =БС((11/12))%; 5*12; -2000; ;1). Ответ. Через 5 лет на счете будет 160 493,99 руб. В задаче указана годовая процентная ставка, но поскольку вложения производятся каждый месяц, ее нужно скорректировать. Поэтому в формуле аргумент ставка =(11/12)%. Кроме того нужно скорректировать количество периодов: вложения производятся каждый месяц в течение 5 лет, всего периодов 5*12. Аргумент плт задан со знаком «-», поскольку деньги отдают. Аргументу тип задано значение 1, что говорит о том, что вложения производятся в начале каждого периода. Задача 8 Рассмотрим предыдущую задачу с небольшим дополнением. Счет был открыт 3 года назад и на настоящий момент на нем 10000 рублей. Используем формулу =БС((11/12))%; 5*12; -2000; -10000; 1). Ответ. Через 5 лет на счете будет 177 783,15 руб. Финансовая функция ПЛТ Функция вычисляет величину выплаты за один период годовой ренты (например, регулярных платежей по займу) при постоянной процентной ставке, т. е. функция ПЛТ вычисляет размер периодической выплаты, необходимой, например, для погашения ссуды за указанное число периодов. Синтаксис: =ПЛТ(ставка;кпер;пс;бс;тип) здесь ставка – процентная ставка за период; кпер - общее число периодов выплат по займу; пс - текущее значение, то есть общая сумма, которую составят будущие платежи. Приведенная (нынешняя) стоимость – общая сумма на настоящий момент, равноценная серии будущих выплат; бс - будущая стоимость или баланс наличности, который нужно достичь после последующей выплаты (бс=0, если значение не указано); тип - (0 или1) Если оплата производится в конце периода, то тип=0 (или значение опущено), если в начале периода - тип=1. Если бс=0 и тип=0, то ПЛТ возвращает значение 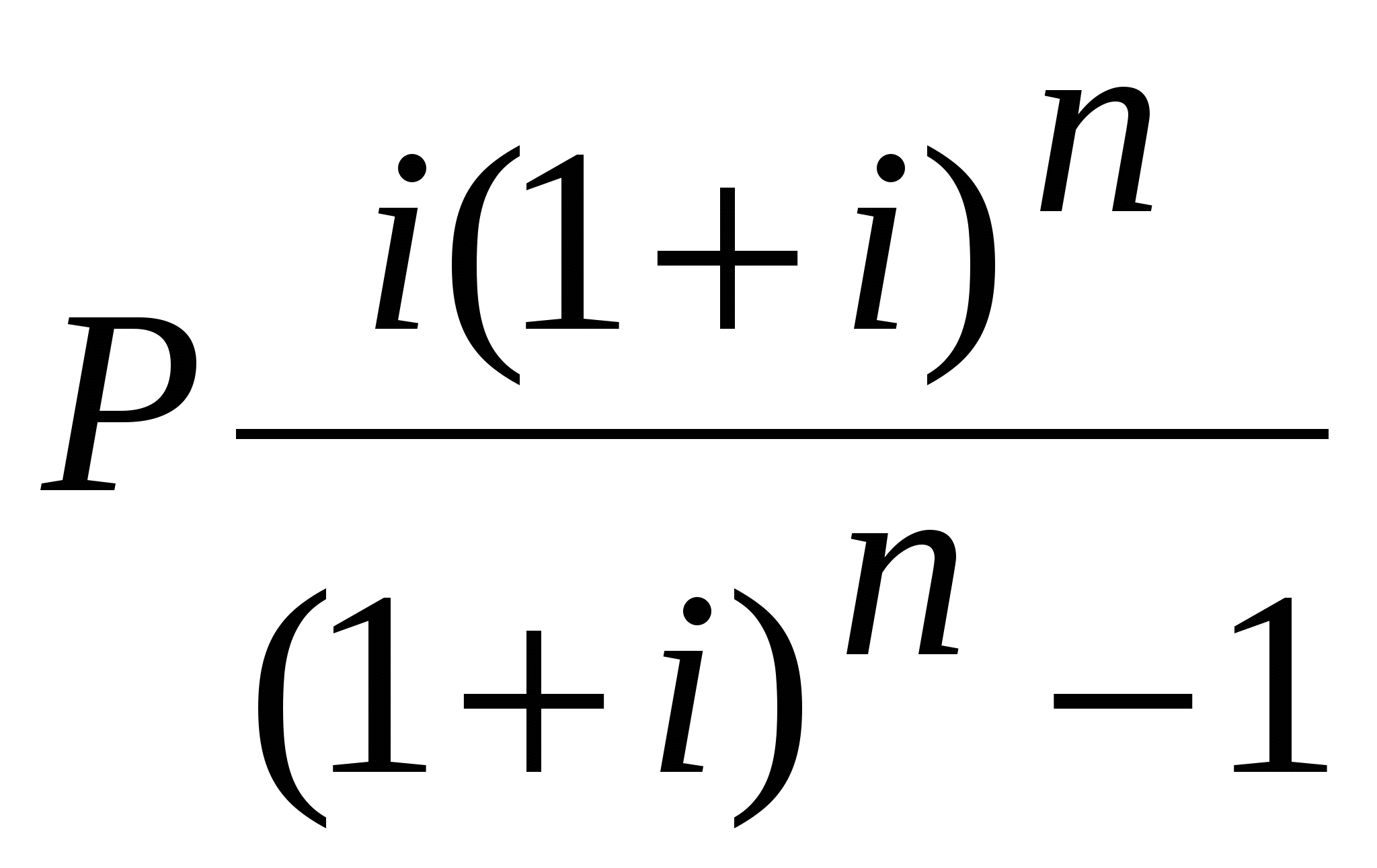 , , где Р – пс, i – ставка, п– число периодов. Задача 9 Нужно взять 25-летнюю ссуду в размере 100000 рублей. Процентная ставка составляет 8%. Какой будет величина ежемесячных выплат. Используя функцию ПЛТ, получим: =ПЛТ((8/12)%; 25*12; 100000) Ответ. -771,82 (отрицательное значение говорит о том, что деньги нужно отдавать). Задача 10 Рассчитать 30-летнюю ипотечную ссуду со ставкой 8% годовых при начальном взносе 20% и ежемесячной (ежегодной) выплате. Размер ссуды – 250000 рублей. Решение.
=ПЛТ((8/12)%;30*12;200000) Ответ. а) -1467,53 р.– ежемесячные платежи; б) общая сумма выплат -1467,53*360 (месяцев)=-528310,49 рублей в) общая сумма комиссионных 528310,49 – 200000 =328310,49 руб.
а) =ПЛТ(8%;30;200000), то есть -17765,49 рублей; б) общая сумма выплат -17765,49*30=-532964,60 рублей в) общая сумма комиссионных 532964,60-200000=332964,6 рублей Функция КПЕР Вычисляет, сколько периодов необходимо для погашения ссуды при заданной величине периодических выплат. Синтаксис: =КПЕР(ставка;плт;пс;бс;тип) Задача 11 За какой срок будет погашен долг в размере 100000 рублей, взятых под 8% годовых, если выплачивать ежемесячно по 1000 рублей. Воспользуемся формулой =КПЕР((8/12)%; -1000; 100000), которая даст ответ 165,34 месяцев. 2.Функции для вычисления скорости оборота Функция СТАВКА Позволяет определить скорость оборота (норму прибыли) вложения по ряду постоянных периодических платежей или/и по единовременной выплате, то есть функция вычисляет процентную ставку за один период, необходимую для получения определенной суммы в течение заданного срока путем постоянных взносов. Синтаксис: =СТАВКА(кпер; плт; пс; бс; тип; предположение) плт - используется при определенной скорости оборота для ряда постоянных периодических выплат; бс - используется при определении скорости оборота для единовременной выплаты; прогноз – (по умолчанию равен 10%) дает начальное приближение нормы, т.к. Excel использует итерационный процесс для вычисления. Задача 12 Рассматривается вложение, которое гарантирует пять ежегодных выплат по 1000 рублей. Сумма вложения составляет 3000 рублей. Чтобы определить годовую скорость оборота этого вложения, используется формула =СТАВКА(5; 1000, -3000). Эта формула возвращает значение 20%. Задача 13 Рассмотрим задачу 12 со следующими изменениями: если вложить 3000 р., то через 5 лет можно получить 5000 р. Определить скорость оборота. Решить задачу поможет формула =СТАВКА(5; ; -3000; 5000). Скорость оборота денег составляет 11%.
Амортизация – это способ, с помощью которого компания может распределить стоимость активов по всему периоду предполагаемого срока их эксплуатации. Другими словами, амортизация представляет собой уменьшение стоимости имущества в процессе эксплуатации. Для определения размера амортизации за год нужно знать:
Есть два основных метода распределения стоимости активов по периоду, в течение которого они будут эксплуатироваться, - метод равномерного начисления износа и метод ускоренной амортизации. При описании функции для вычисления амортизации будут использоваться аргументы, описание которых приведено в таблице.
Функция АПЛ Синтаксис: =АПЛ( стоимость; остаток; время жизни ) Функция АПЛ реализует метод прямолинейной амортизации (метод равномерного начисления), который заключается в следующем. Из суммы стоимости имущества вычитается его остаточная стоимость, а полученная разница делится на количество лет эксплуатации. Метод прямолинейной амортизации предполагает, что амортизация постоянна для любого конкретного единичного периода на протяжении полезного времени жизни имущества. Задача 14 Пусть вы купили компьютер за 40000р., имеющий время жизни 5 лет и ликвидную стоимость 1000р. Определить годовую амортизацию компьютера. Формула =АПЛ(40000; 1000; 5) дает ответ: снижение стоимости компьютера для каждого года эксплуатации составит 7800р. Необходимо отметить, что в Excel имеются функции, вычисляющие амортизацию более сложными методами. |
