Практикум по курсу "Основы теории управления" для студентов заочной формы обучения

• Название: Практикум по курсу "Основы теории управления" для студентов заочной формы обучения
• Дата: 22.05.2021
• Размер: 0.75 Mb.
• Имя файла: Lr_TU_Sukhov_7363.docx
• Тип: Практикум; #208454

Кафедра Автоматики и процессов управления

Лабораторный практикум по курсу

“Основы теории управления”

для студентов заочной формы обучения

Вариант № 14

Выполнил

Ст. гр. 7363

Сухов Р.А.

Преподаватель

Новожилов И.М.

СПбГЭТУ «ЛЭТИ»

2020

1. Выражения связывают управляющий сигнал u(t) на выходе регулятора с сигналом e(t) на его входе и описывают типовые законы (алгоритмы) управления.

Который их них соответствует интегральному закону ?

2. Модель СУ задана структурной схемой  рис.1.

О
ператоры звеньев (блоков) заданы передаточными функциями (ПФ).

Звено 1 – “сумматор”. Его ПФ W₁(s) = 1/1 = 1.

Значения параметров ПФ остальных звеньев:

W₂(s)=K_1=10,

W₃(s)=K₂/(T₁s+1)=5/(2s+1),

W₄(s)=K₃/(T₂s+1)=1/(0.1s+1).

W₅(s)=K₄/(T₃s+1)=0.4/(0.01s+1).

К какому классу (классам) относится математическая модель СУ ?

1: линейные; 2: непрерывные; 3: дискретные, 4: нелинейные.

Данная СУ ?

1: статическая, 2: с астстизмом 1-го порядка, 3: с астстизмом 2-го порядка.

С использованием графического редактора программы CLASSiC сформировать модель системы в соответствии со структурной схемой рис.1 и заданными операторами звеньев. Модель сохранить в файле, присвоив ей конкретное имя.

Модель сохранена в файле Lab.mdl.

Вид структурной схемы из графического редактора программы CLASSiC приведен на рис.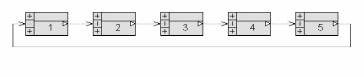

Рис.1а

Для контроля правильности ввода получить модель в текстовой форме из окна графического редактора моделей, команды меню “Вид””Модель – текстовая форма (сводка)”.

Модель: Lab.MDL

========================

Количество блоков: 5

Количество связей: 5

=========================================================

| | Передаточные функции | |

| Блоки |-------------------------------| Связи |

| | Числитель |Знаменатель|Степень| |

=========================================================

| #1 | 1 | 1 | 0 | 2 |

| Вход | | | | |

|------------|-----------|-----------|-------|----------|

| #2 | 10 | 1 | 0 | 3 |

|------------|-----------|-----------|-------|----------|

| #3 | 5 | 1 | 0 | 4 |

| | | 2 | 1 | |

|------------|-----------|-----------|-------|----------|

| #4 | 1 | 1 | 0 | 5 |

| | | 0.1 | 1 | |

|------------|-----------|-----------|-------|----------|

| #5 | 0.4 | 1 | 0 | -1 |

| Выход | | 0.01 | 1 | |

=========================================================

Убедиться в соответствии таблицы заданной модели СУ.

3. Модель СУ задана в вопросе2 (рис.2). Какой принцип управления реализован ? 1принцип разомкнутого управления, 2  принцип компенсации, 3принцип замкнутого управления (принцип обратной связи), 4  принцип комбинированного управления (одновременная реализация в СУ принципов 2 и 3).

4. На рис.2 показана общая структура, которая получена из модели задачи2.

В
ыразить через численные значения параметров звеньев передаточную функцию W_P(s)=B_P(s)/A_P(s) разомкнутой СУ (т.е. системы без обратной связи).

.
Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 20 | 1 | 0 |

| | | 2.11 | 1 |

| | | 0.221 | 2 |

| | | 0.002 | 3 |

================================================

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полностью совпадают.

5. Структурная схема СУ представлена на рис.2. Записать формулу, связывающую ПФ по управлению Ф(s)=Y(s)/F(s) замкнутой системы и ПФ W_P(s) разомкнутой системы.

Ф(s) = W_P(s) /(1+W_P(s)).

Записать через численные значения параметров звеньев ПФ Ф(s) для СУ, заданной в задаче 2.

Ф(s)= .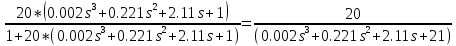

Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 20 | 21 | 0 |

| | | 2.11 | 1 |

| | | 0.221 | 2 |

| | | 0.002 | 3 |

================================================

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полностью совпадают.

6. Структурная схема СУ представлена на рис.2. Записать формулу, связывающую ПФ по ошибке Ф_e(s)=E(s)/F(s) замкнутой системы и ПФ W_P(s) разомкнутой системы.

Ф_e(s) = 1/(1 + W_P(s)).

Записать через численные значения параметров звеньев ПФ Ф_e(s) для СУ, заданной в задаче 2.

Ф_e(s)= .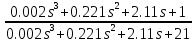
Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 1 | 21 | 0 |

| | 2.11 | 2.11 | 1 |

| | 0.221 | 0.221 | 2 |

| | 0.002 | 0.002 | 3 |

================================================

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полностью совпадают.

7. Модель системы задана в задаче 2. На вход системы подается единичное ступенчатое воздействие f(t)=1(t) (изображение этой функции F(s) = 1/s). Чему равно значение установившейся ошибки ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.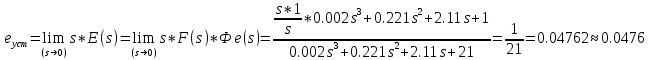

.

На рис.3 приведены графики процессов в системе и показана установившаяся ошибка.


Рис.3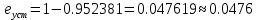

.

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полностью совпадают.

8. Модель системы задана в задаче 2. На вход системы подается воздействие с постоянной скоростью f(t)=at=1t (изображение F(s)=a/s²). Чему равно значение установившейся ошибки ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.

.

На рис.4 приведены графики процессов в системе и показана установившаяся ошибка.

Рис.4

По графику видно, что

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полностью совпадают.

9. Модель замкнутой СУ задана в вопросе 2. В каких рассмотренных выше задачах фигурирует характеристический полином системы?

В задачах №5, 6, 7, 8 в выражениях .

10. Модель СУ задана в вопросе 2. Провести анализ устойчивости этой системы. Использовать алгебраический критерий Гурвица.

1: система устойчива,

2: система нейтральна (находится на нейтральной границе устойчивости),

3: система находится на колебательной границе устойчивости,

4: система неустойчива.

Для устойчивости СУ необходимо и достаточно, чтобы корни характеристического полинома принадлежали левой полуплоскости плоскости корней. В характеристическом полиноме: – коэффи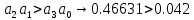циенты и все коэффициенты => СУ устойчива.

11. Модель СУ задана в вопросе 2. Усиление в контуре обратной связи K=K_1K_2K_3K₄. Есть возможность изменять (варьировать) параметр K₁. K_{кр } “критический” коэффициент усиления контура, при котором система находится на колебательной границе устойчивости. Чему равно значение K=K_кр ? Использовать алгебраический критерий Гурвица.

K_кр= .

На рис.5 приведены графики процесса в системе при K=K_кр.



Рис. 5

Модель: "Lab.MDL"

================================

Ном. Система

Нули:

Корни отсутствуют - полином нулевой степени

Полюсы:

p1 = 0.000000 + 32.480699j

p2 = 0.000000 – 32.480699j

p3 = -110.499962

Абсолютное затухание: 0

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Результаты полностью совпадают.

12. Модель СУ задана в вопросе 2. Изменяем оператор звена 5. Полагаем T_3=0. В результате имеем W₅(s)=K₄.

Определить область устойчивости для коэффициента усиления контура – интервал значений (K_minKK_max), при котором система устойчива.

1: (0K1.25); 2: (0K100); 3: (0K); 4: (K).

.

.

.

.

Достаточным и необходимым условием устойчивости СУ для полинома второго порядка одинаковый знак у всех коэффициентов. Отсюда следует, что может быть любым положительным числом.

13. Модель замкнутой СУ задана в вопросе 2.

Построить с использованием программы CLASSiC амплитудную L_р() и фазовую _р() логарифмические частотные характеристики разомкнутой системы.



1/T₁
Скопировать график в данный отчет. На этом же графике с помощью средств рисования WORD построить асимптотическую ЛАХ, обозначить графики и показать запас по фазе (если система устойчива).

На рис.6 приведены результаты расчета и требуемые построения.

Результат автоматизированного расчета:

Частота среза: 7.8326 рад/с

Запас по фазе: 51.1038 град

Частота пи: 32.4808 рад/с

Запас по модулю: 21.2950 дБ

13. На рис.7 построены качественно амплитудно-фазовые частотные характеристики W_P(j) разных разомкнутых СУ.

К
оторая из этих характеристик соответствует системе, заданной в задаче 2 ?

1; 2; 3; 4.



Рис. 7.1

14. Модель СУ задана в вопросе 2. Изменяем оператор звена 5. Полагаем T_3=0. В результате имеем W₅(s)=K₄.

Которая из частотных характеристик, изображенных на рис.7, соответствует такой системе?

1; 2; 3; 4.



Рис. 7.2

15. На рис.8 построена качественно амплитудно-фазовая частотная характеристика W_P(j) некоторой разомкнутой СУ.

П
роанализировать устойчивость системы в замкнутом состоянии. Использовать критерий Найквиста.

1: система устойчива,

2: система нейтральна (находится на нейтральной границе устойчивости),

3:система находится на колебательной границе устойчивости,

4: система неустойчива.

Система находится на колебательной границе устойчивости, так как проходит через критическую точку -1.