Практикум по предмету СК СПРС. Практикум по курсу средства коммутации систем подвижной радиосвязи
 Скачать 85.91 Kb. Скачать 85.91 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное агентство по образованию ГОУ ВПО « Юго-Западный государственный университет» Факультет ИиВТ Кафедра телекоммуникаций ПРАКТИКУМ ПО КУРСУ «СРЕДСТВА КОММУТАЦИИ СИСТЕМ ПОДВИЖНОЙ РАДИОСВЯЗИ» Курск 2012 УДК 621.3.014.22(076.5) Составитель: В.Л.Лысенко Практикум «Исследование характеристик систем пространственной и временной коммутации» по дисциплине «Средства коммутации систем подвижной радиосвязи». - Курск: 2012. -52 с. Данный практикум предназначен для студентов специальностей 210402, 210404 и других специальностей вуза по направлению «Телекоммуникации» с целью изучения принципов построения коммутационных схем и расчета их пропускной способности, длин очередей, вероятностей блокировок и особенностей реализации схем пространственной и временной коммутации. Табл.2. Ил.29 . Библиогр.: 10 назв. Практическая работа № 1 Построение многозвенных коммутационных схем пространственной коммутации и определение их параметров
Ознакомление с принципами построения и работы многозвенных коммутационных схем, а также с методикой оценки их параметров. Перед выполнением лабораторно-практических заданий студенты должны ориентироваться в основных аспектах теории вероятностей, графов, теории массового обслуживания на примерах систем с отказами и с очередями, обладать навыками программирования и функционального моделирования в программных средах MathCad/ Matlab (пакет Simulink)/LabVIEW. В результате выполнения практического задания студенты должны освоить принципы реализации многозвенных коммутационных схем и методы их анализа в программных средах MathCad/ Matlab (пакет Simulink)/ LabVIEW. 1.2. Краткие теоретические сведения Многозвенные коммутационные схемы позволяют использовать совокупность точек коммутации для образования нескольких соединительных путей через коммутационную схему. Структурная схема трехзвенной коммутационной схемы показана на рис. 1.1, входы и выходы в которой разделены на подгруппы из n входов и n выходов каждая [4]. Входы каждой подгруппы обслуживаются отдельной прямоугольной коммутационной схемой. Входные коммутаторы – это коммутаторы n·k, где каждый из k-ых выходов соединяется со входом одного из k коммутаторов центрального звена.  Рис. 1.1. Трехзвенная коммутационная схема Третье звено состоит из коммутаторов k·n, которые обеспечивают соединение каждого коммутатора центрального звена с группой n выходов. Все коммутаторы центрального звена имеют параметры (N/n)·(N/n), что позволяет обеспечить соединение любого коммутатора первого звена с любым коммутатором третьего звена. Если все коммутаторы являются полнодоступными коммутационными схемами, то любое конкретное соединение входа с выходом схемы может быть установлено k различными путями. Каждый из k путей проходит через отдельный коммутатор центрального звена. Поскольку каждая входящая и исходящая линия связи подключается к ограниченному числу точек коммутации, то минимизируется и емкостная нагрузка. Общее число точек коммутации Nx, требуемое для построения трехзвенной коммутационной схемы составляет [4]: Nx=2·N·k+k·(N/n)2 , (1) где N – число входов (выходов); n – размер каждой группы входов выходов); k – число коммутаторов центрального звена. Число точек коммутации, определенное таким образом, может быть значительно меньше числа точек коммутации, требуемого для построения однозвенных коммутационных схем. Однако вначале следует определить, сколько коммутаторов центрального звена должна содержать схема, чтобы обеспечить приемлемое качество обслуживания. Если допускается совместное использование точек коммутации, то возникает возможность блокировки. Неблокирующиеся коммутационные схемы являются одним из привлекательных свойств однозвенной коммутационной схемы. Если каждый отдельный коммутатор является неблокирующейся схемой, и при этом число коммутаторов центрального звена k равно 2·n–1, то коммутационная схема будет строго неблокирующейся. Подставляя в (1) вместо k его выражение (k = 2 · n – 1) в итоге получаем, что общее число точек коммутации в строго неблокирующейся трехзвенной коммутационной схеме равно: Nx=2·N·(2·n-1)+(2·n-1)·(N/n)2 (2) Выражение для минимального числа Nx_minточек коммутации трехзвенной неблокирующейся схемы определяют, находя экстремум функции Nx (дифференцируя выражение (2) и приравнивая его к «0» [4]): Nx min = 4·N· (2·N – 1)½, (3) где N – общее число входов (выходов). Трехзвенная коммутационная схема обеспечивает значительное уменьшение числа точек коммутации, особенно при большой емкости коммутационной схемы.
Практическая работа № 2 Расчет вероятностей блокировок многозвенных коммутационных схем по методу графов Ли
Ознакомление с подходом к оценке вероятностей блокировок многозвенных коммутационных схем по методу графов Ли. Перед выполнением лабораторно-практических заданий студенты должны ориентироваться в основных аспектах теории вероятностей, графов, теории массового обслуживания на примерах систем с отказами и с очередями, обладать навыками программирования и функционального моделирования в программных средах MathCad/ Matlab (пакет Simulink)/LabVIEW. В результате выполнения практического задания студенты должны освоить принципы определения вероятностей блокировок многозвенных коммутационных схем по методу графов Ли и анализа характера их зависимостей в программных средах MathCad/ Matlab (пакет Simulink)/ LabVIEW. 2.2. Краткие теоретические сведения Для сокращения числа точек коммутации применяются схемы с двумя и более звеньями. Даже для трехзвенных коммутационных схем большой емкости число точек коммутации может быть недопустимо большим. В этом случае наиболее существенное уменьшение числа точек коммутации может быть достигнуто не столько за счет введения дополнительных звеньев в коммутационную схему, сколько за счет работы коммутационной схемы с приемлемо малым значением вероятности блокировки. Одним из наиболее гибких и логически простых методов вычисления вероятности блокировок является метод, основанный на использовании вероятностных графов, предложенный Ли [4]. Если какая-либо одна из группы n параллельных линий может быть использована при установлении соединения, то полная вероятность блокировки В есть вероятность того, что все n линий заняты: В = рn , где р – вероятность того, что линия занята. Если при установлении соединения необходимо использовать n последовательно соединенных линий, то вероятность блокировки определяется как: B=1–qn, (2.1) где q=1–р – вероятность того, что линия свободна. Вероятностный граф трехзвенной коммутационной схемы изображен на рис. 2.1 и показывает, что любое соединение может быть установлено k различными путями: каждый путь проходит через один коммутатор центрального звена. Вероятность того, что любая промежуточная линия занята, обозначается через p1.  Рис. 2.1 Вероятностный граф трехзвенной коммутационной схемы Вероятность блокировки трехзвенной схемы может быть определена как: В = (1-(q1)2)k , (2.2) где k – число коммутаторов центрального звена, и q1 = 1 - p1 – вероятность того, что промежуточная линия свободна. Если известна вероятность р того, что занят вход, то вероятность p1 того, что занята промежуточная линия, можно определить как: p1 = p/β, (2.3) где β = k/n – коэффициент расширения. Это выражение показывает, что, если занято некоторое число входов, то также занято такое же число выходов из коммутатора первого звена. Величина β определяется на основе допущения, что k больше n: это означает, что на первом звене коммутационной схемы имеет место пространственное расширение. Если же β меньше 1, то это означает, что на первом звене осуществляется концентрация поступающей нагрузки. Окончательная формула для вероятности блокировки трехзвенной коммутационной схемы, выраженная через использование входящих линий р: В = [1- (1- p / β)2] · k . (2.4) Если средние три звена пятизвенной коммутационной схемы являются строго неблокирующимися (k2 = 2·n2 - 1), то такая структура позволяет получить экономию точек коммутации на каждом коммутаторе центрального звена рассмотренной ранее трехзвенной коммутационной схемы. Вероятностный граф пятизвенной схемы приведен на рис. 2.2 (см. ниже). На основе этого графа вероятность блокировки может быть оценена следующим образом: B = {1-(q1)2·[1-(1- q22)k2 ]}k1, (2.5) где q1 = 1 – p1 и q2 = 1 – p2 . 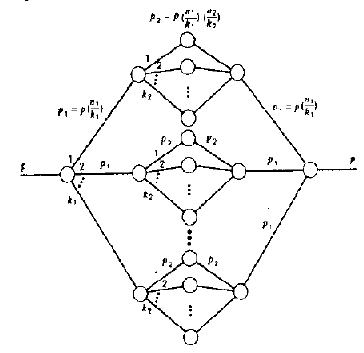 Рис. 2.2. Вероятностный граф пятизвенной коммутационной схемы
2.4. Контрольные вопросы 1. В чем суть оценки вероятности блокировки по методу Ли на примере трехзвенной коммутационной схемы? 2. Показать, в каких ситуациях возникает необходимость в переходе от трехзвенной коммутационной схемы к пятизвенной. 3. Что такое пространственное расширение и концентрация поступающей нагрузки и для каких случаев их используют?
Практическая работа № 3 Расчет вероятностей блокировок многозвенных коммутационных схем по методу Якобеуса 3.1. Цель практической работы: Ознакомление с методом оценки вероятностей блокировок многозвенных коммутационных схем по методу Якобеуса. Перед выполнением лабораторно-практических заданий студенты должны ориентироваться в основных аспектах теории вероятностей, графов, теории массового обслуживания на примерах систем с отказами и с очередями, обладать навыками программирования и функционального моделирования в программных средах MathCad/ Matlab (пакет Simulink)/LabVIEW. В результате выполнения практического задания студенты должны освоить принципы определения вероятностей блокировок многозвенных коммутационных схем по методу Якобеуса и анализа характера их зависимостей в программных средах MathCad/ Matlab (пакет Simulink)/ LabVIEW. 3.2. Краткие теоретические сведения Выражение для вероятности блокировки, полученное на основе метода графов Ли (вероятностного графа Ли), было определено с учетом ряда предположений, означающих, что отдельные вероятности принимаются независимыми. На самом же деле эти вероятности не являются независимыми, особенно в тех случаях когда в схеме используется значительное расширение. При наличии в схеме пространственного расширения предположение о независимости отдельных вероятностей приводит к завышению значения вероятности потерь по сравнению с фактическим. Анализ многозвенных коммутационных схем был выполнен в 1950 г. Якобеусом, который в итоге привел к следующему результату для вероятности блокировки [4]: 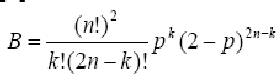 , (3.1) , (3.1)где n – число входов (выходов) коммутатора первого (третьего) звеньев; k – число коммутаторов второго звена; р – вероятность занятости входа. Получаемые обоими методами (графов Ли и Якобеуса) результаты хорошо согласуются с практическими в случае, когда коэффициенты расширения β близки к единице. Во всех случаях, когда β больше 1 эффективнее использование метода Якобеуса.
Библиографический список 1. Матвеев В.Ф., Ушаков В. Г. Системы массового обслуживания. – М.: МГУ, 1984. 2. Тихоненко О.М. Модели массового обслуживания в системах обработки информации. – Минск: Университет, 1990. 3. Абилов А.В. Сети связи и системы коммутации. – Ижевск: Изд-во ИжГТУ, 2002. 4. Беллами Дж. Цифровая телефония. - М.: Эко-Трендз, 2004. 5. Берлин Л.Н. Коммутация в системах и сетях связи. - М.: Эко-Трендз, 2006. 6. Гольдштейн Б.С. Системы коммутации. 2-е изд., испр. и доп. СПб.: BHV-2004. 7. Букрина Е.В. Сети связи и системы коммутации: Учебное пособие / Е.В. Букрина. - Екатеринбург: УрТИСИ ГОУ ВПО «СибГУТИ», 2007. 8. Аваков Р. А., Шилов О. С., Исаев В. И. Основы автоматической коммутации: Учебник для, вузов. — М.: Радио и связь, 1981. 9. Автоматическая коммутация: Учебник для вузов./ Под ред. О.Н.Ивановой. -М.: Радио и связь,1988. 10. Виноградова Н.А., Листратов Я.И., Свиридов Е.В. Разработка прикладного программного обеспечения в среде LabVIEW: Учебное пособие.– М.: Изд-во МЭИ, 2005. 10. Загидуллин Р.Ш. LabVIEW7 в исследованиях и разработках. -М.: Горячая линия – Телеком, 2005. |
