Практикум по напорной гидравлике и гидромашинам учебное пособие

• Название: Практикум по напорной гидравлике и гидромашинам учебное пособие
• Дата: 31.03.2023
• Размер: 4.09 Mb.
• Имя файла: virtualnyj-laboratornyj-praktikum_color.docx
• Тип: Практикум; #1027990
• страница: 12 из 31

Виртуальная лабораторная работа № 5

ИЗУЧЕНИЕ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ НАПОРНОГО ТРУБОПРОВОДА С ОПРЕДЕЛЕНИЕМ КОЭФФИЦИЕНТОВ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ И МЕСТНЫХ СОПРОТИВЛЕНИЙ
Вводная часть

Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора (энергии) затрачивается на преодоление работы сил вязкости, т. е. возникают потери напора.

При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им потери напора ‒ потерями напора по длине (h_l). Эти потери в круглых трубопроводах, работающих полным сечением, вычисляют по формуле Дарси ‒ Вейсбаха:

ℎ_𝑙

= 𝜆 ^𝑙

𝑑

^𝑣2 , (16)

2𝑔

где ‒ безразмерный коэффициент, называемый коэффициентом гидравлического трения (коэффициентом Дарси). Величина коэффициента

 характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса Re и относительной шероховатости _э/d трубопровода, т. е. = f(Re, _э/d); l и d – длина и внутренний диаметр трубопровода; ʋ – средняя скорость движения потока жидкости [2, 5, 9].

Впервые зависимость = f(Re) исследовал И.И. Никурадзе (рис. 9), который проводил опыты на трубах с искусственными шероховатостями.

Величину коэффициента при гидравлических экспериментах вычисляют по опытным данным из формулы (16). При гидравлических же расчетах – по эмпирическим и полуэмпирическим формулам, например при ламинарном режиме:

𝜆 = ⁶⁴ , (17)

𝑅𝑒

а при турбулентном режиме движения жидкости и работе трубопровода в

области доквадратичного сопротивления – по формуле А.Д. Альтшуля:

𝜆 = 0,11 ^∆э + ⁶⁸



0,25

. (18)

докв

𝑑 𝑅𝑒

Величину абсолютной эквивалентной шероховатости _эпри расчетах берут из справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла _э= 0,006 мм, а для стальных водопроводных умеренно заржавленных труб _э= 0,20…0,50 мм.

Область гидравлического сопротивления при расчетах определяют или непосредственно по графикам = f(Re,_э/d), полученным опытным путем для труб из различных материалов и приведенным в справочной

литературе, или же с помощью соотношений ^10𝑑

∆_э

и ^500𝑑, предложенных

∆_э

А.Д. Альтшулем на основе использования упомянутых графиков. В

последнем случае вычисляют соотношения ^10𝑑

∆<sub>э

и</sub> 500𝑑

∆_э

и сравнивают их с

числом Рейнольдса 𝑅𝑒_(𝑑) = ^𝑣𝑑. При этом, если 𝑅𝑒 ≥ ^500𝑑, трубопровод

𝜈 ∆_э

работает в области квадратичного сопротивления. Если 3000 < 𝑅𝑒 ≤ ^10𝑑,

∆_э

трубопровод работает в области гидравлически гладких труб. Если же

^10𝑑 < 𝑅𝑒 < ^500𝑑, трубопровод работает в области доквадратичного

∆_э ∆_э

сопротивления.

Следует иметь в виду, что для каждой области гидравлического сопротивления предложены и используются при гидравлических расчетах свои формулы для вычисления коэффициента .

Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока, изменения скорости потока по величине или направлению, называют местными сопротивлениями, а вызываемые ими потери напора ‒ местными потерями напора (h_м).

При прохождении через любое местное сопротивление поток жидкости деформируется (рис. 10), вследствие чего движение становится неравномерным, резко изменяющимся, для которого характерны:

а) значительное искривление линий тока и живых сечений потока;

б) отрывы транзитной струи от стенок трубопровода (ввиду действия закона инерции) и возникновение в местах отрыва устойчивых водоворотов;

в) повышенная (по сравнению с равномерным движением) пульсация скоростей и давлений;

г) изменение формы (переформирование) эпюр скоростей.

Местные потери напора при гидравлических расчетах вычисляют по формуле Вейсбаха:


м
ℎ = ^𝑣2 , (19)

2𝑔

где ‒ безразмерный коэффициент, называемый коэффициентом местного сопротивления; υ ‒ средняя скорость потока в сечении за местным сопротивлением, т. е. ниже по течению (если скорость υ, как исключение, принимается перед местным сопротивлением, это обязательно оговаривается) [2, 5, 9].

Величина коэффициента зависит в общем случае от числа Рейнольдса Re, вида и конфигурации, т. е. формы проточной части местного сопротивления. В частном случае, когда трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, величина коэффициента от Re не зависит.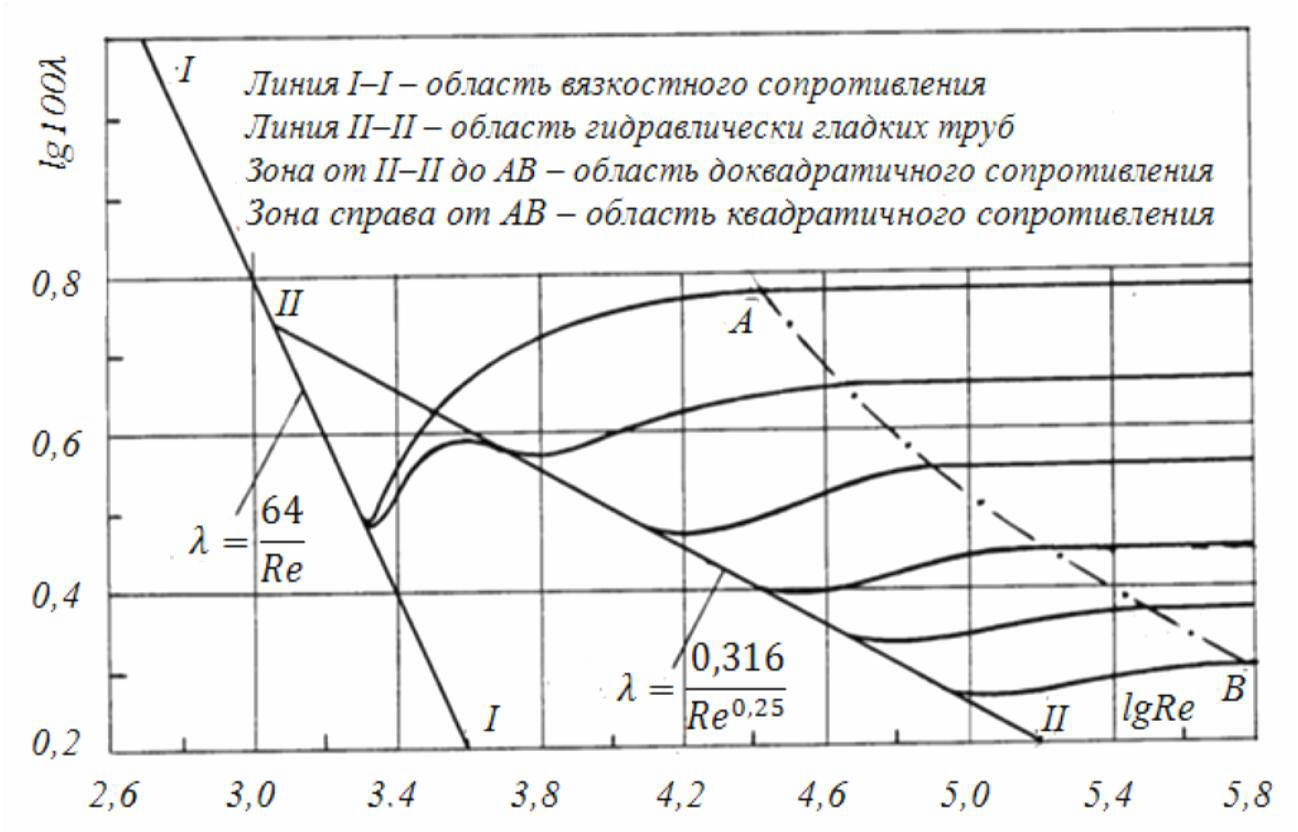

Рис. 9. График зависимости коэффициента гидравлического трения λ от числа Рейнольдса Re для труб с различной относительной искусственной шероховатостью _э /d (график И.И. Никурадзе)




а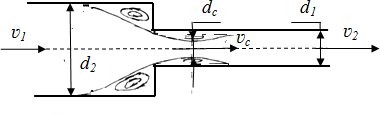




б

Рис. 10. Схемы движения жидкости при резком (внезапном) изменении сечения трубопровода: а – резкое расширение; б – резкое сужение
Величину для каждого вида местного сопротивления определяют по данным гидравлических экспериментов, пользуясь формулой (19). Полученные таким образом значения коэффициентов для различных видов местных сопротивлений берутся при гидравлических расчетах (обычно при квадратичной области сопротивления) из справочной и специальной литературы. Исключением являются резкое расширение и резкое сужение трубопровода, для которых численные значения коэффициентов определяются по формулам, полученным теоретическим и полуэмпирическим путем. При резком расширении трубопровода, когда средняя скорость в формуле (19) взята перед местным сопротивлением, т. е. ʋ₁, коэффициент местного сопротивления для резкого расширения

^` = 1 − ^𝑆1



2

, (20)

pp _𝑆2

где S₁ и S₂ ‒ площади проходных сечений трубопровода до и после местного сопротивления по направлению движения жидкости соответственно.

Если же скорость берется за местным сопротивлением, т. е. ʋ₂, то

^`` = ^𝑆2 − 1



2

. (21)

pp _𝑆1

Коэффициент местного сопротивления при резком сужении трубопровода (_рс) принято относить к скорости после сужения. При этом

 = 0,5 1 − ^𝑆2


2

. (22)

рс _𝑆1