Практикум по напорной гидравлике и гидромашинам учебное пособие
 Скачать 4.09 Mb. Скачать 4.09 Mb.
|
Виртуальная лабораторная работа № 4ЭКСПЕРИМЕНТАЛЬНАЯ ИЛЛЮСТРАЦИЯ ЛАМИНАРНОГО И ТУРБУЛЕНТНОГО РЕЖИМОВ ДВИЖЕНИЯ ЖИДКОСТИ, УСТАНОВЛЕНИЕ ЗАКОНОВ ГИДРАВЛИЧЕСКОГО СОПРОТИВЛЕНИЯ И ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОГО ЧИСЛА РЕЙНОЛЬДСА Вводная часть Многочисленными экспериментальными исследованиями установ- лено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме. Ламинарный режим наблюдается при небольших скоростях движения. При этом окрашенные струйки жидкости не перемешиваются, сохраняя траекторию своего движения по всей длине потока, т. е. движение жидкости при ламинарном режиме является струйчатым, перемешивание частиц жидкости отсутствует. Турбулентный режим наблюдается при значительных скоростях и характеризуется интенсивным перемешиванием частиц жидкости, что обусловливает пульсацию скоростей и давления. Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической ‒ ʋкр. Величина ее, как показывают опыты в трубопроводах круглого сечения, зависит от рода жидкости, характеризуемого динамическим коэффициентом вязкости и плотностью , а также от диаметра трубопровода d. Одновременно опытами установлено, что величина безразмерного алгебраического комплекса, называемого критическим числом Рейнольдса, отвечающего критической скорости 𝑣кр: 𝑅𝑒кр(𝑑) = 𝑣кр𝜌𝑑  𝜇 𝜇= 𝑣кр𝑑 . (14)  𝜈 𝜈Для напорных потоков критическое число Рейнольдса Reкр(d) = 2320. Устойчивый ламинарный режим движения жидкости наблюдается  𝜈 при значениях числа Рейнольдса 𝑅𝑒(𝑑) = 𝑣𝑑 < 𝑅𝑒кр(𝑑) ≈ 2320, а турбу-  𝜈 лентный – при 𝑅𝑒(𝑑) = 𝑣𝑑 > 𝑅𝑒кр(𝑑) ≈ 2320. Таким образом, число Рейнольдса  𝜈 𝑅𝑒(𝑑) = 𝑣𝑑 (15) является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением.  Величину 𝜈 = 𝜇 , имеющую размерность м2/с, входящую в формулы Величину 𝜈 = 𝜇 , имеющую размерность м2/с, входящую в формулы𝜌 и (15), называют кинематическим коэффициентом вязкости жидкости. Из изложенного следует, что для определения режима напорного движения жидкости в круглом трубопроводе достаточно вычислить по формуле (15) число Рейнольдса и сравнить его с критическим [2, 5, 9]. Знание режима движения жидкости необходимо для правильной оценки потерь напора при гидравлических расчетах. Как показывают опыты в круглых трубах при напорном равномерном движении (результаты их представлены на рис. 7 в виде графика зависимости потерь напора по длине hlот средней скорости υ), при ламинарном режиме потери напора hlпропорциональны средней скорости υ в первой степени, а при турбулентном ‒ в степени 1,75 ≤ m ≤ 2. Заметим, что с помощью этого графика определяют величину критической скорости υкр, а через нее ‒ и критическое число Рейнольдса по формуле (14) [6].  Необходимо отметить, что график (см. рис. 7) построен в логарифмических координатах, что способствует преобразованию нелинейных зависимостей в линейные и упрощает обработку опытных данных. Описание установкиУстановка (рис. 8) включает в себя расположенную горизонтально стеклянную трубу, в которой и изучается движение воды при различных режимах, напорный бак, емкость с раствором красителя, подаваемого открытием крана по трубке во входное сечение стеклянной трубы. Для измерения расхода воды в стеклянной трубе служат мерная емкость и секундомер. Вода в напорный бак подается по питающему трубопроводу открытием вентиля из резервуара лаборатории. Для поддержания уровня воды в напорном баке во время опытов на постоянной отметке имеется переливное устройство. Температура воды в напорном баке измеряется термометром. Регулирование расхода воды, а следовательно, и средней скорости ее движения в стеклянной трубе, осуществляется регулирующим вентилем. На стеклянной трубе имеются пьезометры для определения потерь напора по длине hl(по разности их показаний) [6, 12]. 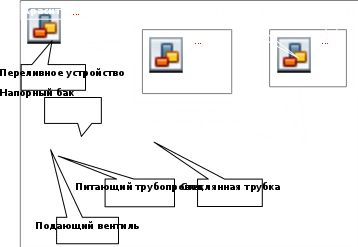 Рис. 8. Схема установки для изучения режимов движения жидкости |
