Практикум по напорной гидравлике и гидромашинам учебное пособие
 Скачать 4.09 Mb.
|
Виртуальная лабораторная работа № 3ОПРЕДЕЛЕНИЕ ОПЫТНЫМ ПУТЕМ СЛАГАЕМЫХ УРАВНЕНИЯ Д. БЕРНУЛЛИ ПРИ УСТАНОВИВШЕМСЯ НЕРАВНОМЕРНОМ ДВИЖЕНИИ ЖИДКОСТИ В НАПОРНОМ ТРУБОПРОВОДЕ (ТРИ СЕЧЕНИЯ) Вводная часть 𝑈 𝑈 Для двух произвольно выбранных живых сечений I‒I и II‒II струйки реальной жидкости при установившемся движении (рис. 4) уравнение Д. Бернулли имеет вид 𝑧1 + 𝑝1 2 +1 = 𝑧2 + 𝑝2 2 +2 + ℎ𝑊 . (12)  𝜌𝑔2𝑔 𝜌𝑔 2𝑔 1−2 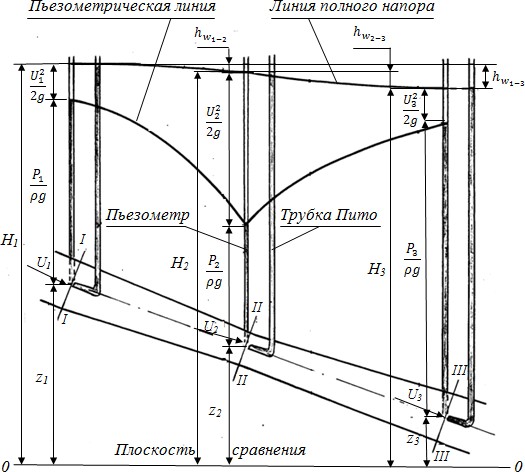 Рис. 4. Диаграмма уравнения Д. Бернулли для струйки реальной жидкости Слагаемые, входящие в уравнение (12), можно истолковать с геометрической и энергетической точек зрения. С геометрической точки зрения слагаемые уравнения (12) являются высотами (напорами): z – геометрическая высота (напор), т. е. превышение центра тяжести рассматриваемого поперечного сечения струйки над плоскостью сравнения 0‒0, выбираемой произвольно; 𝑝𝜌𝑔 – пьезометрическая высота (напор), т. е. высота подъема жидкости в пьезометре, подключенном к центру тяжести рассматриваемого сечения струйки, отвечающая гидродинамическому давлению p в этой точке; 𝑈2  2𝑔 скоростная высота (напор), отвечающая местной скорости U, т. е. скорости в центре тяжести сечения; 𝑧 + 𝑝𝜌𝑔 𝑧 + 𝑝𝜌𝑔 гидростатический напор; + 𝑈2 = 𝐻 – полный напор в рассматриваемом сечении2𝑔 струйки; ℎ𝑊1−2 = 𝐻1 − 𝐻2 – потеря полного напора, т. е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями I‒I и II‒II. С энергетической точки зрения слагаемые уравнения (12) представляют собой разновидности удельной энергии, а именно: z ‒ удельная потенциальная энергия положения жидкости в рассматриваемом сечении струйки; 𝑝𝜌𝑔 удельная потенциальная энергия давления; 𝑧 + 𝑝𝜌𝑔 удельная потенциальная энергия жидкости; 𝑈2 ‒ удельная кинетическая энергия движения жидкости;2𝑔 𝑧 + 𝑝𝜌𝑔 + 𝑈2 = 𝐻 ‒ полная удельная энергия движущейся жидкости; 2𝑔ℎ𝑊1−2 ‒ потеря полной удельной энергии струйки, т. е. части ее, затраченной на преодоление работы сил внутреннего трения, обусловленного вязкостью жидкости. Удельной энергией называется энергия, приходящаяся на единицу веса жидкости. Величины слагаемых уравнения (12) могут быть определены опытным путем следующим образом: z – геометрическим нивелированием или измерением линейкой; 𝑝 𝜌𝑔 𝑈2 2𝑔 с помощью пьезометрической трубки (пьезометра); – по разности отметок уровней жидкости в скоростной и пьезометрической трубках, подключенных к рассматриваемой точке живого сечения струйки; ℎ𝑊1−2 ‒ по разности отметок уровней воды в скоростных трубках, подключенных к сечениям I‒I и II‒II струйки реальной жидкости [2, 5, 9]. Скоростная трубка (трубка Пито) (рис. 5) представляет собой трубку, верхний конец которой открыт в атмосферу, а нижний изогнут навстречу скорости U в рассматриваемой точке потока жидкости. Благодаря этому, у входа в изогнутый конец скоростной трубки кинетическая энергия частицы жидкости преобразуется в потенциальную энергию давления столба жидкости. 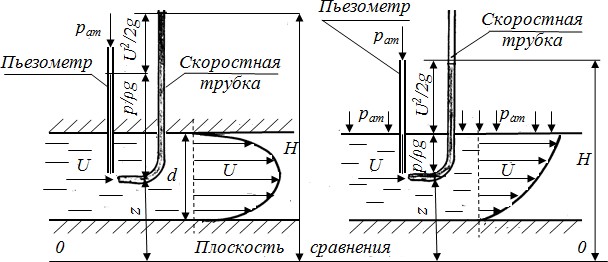 а б Рис. 5. К изменению скоростного напора U2/2g при движении жидкости: а – напорном; б – безнапорном Поскольку срез нижнего конца скоростной трубки перпендикулярен вектору скорости, а срез нижнего конца пьезометра параллелен, уровень жидкости в скоростной трубке всегда устанавливается выше, чем в пьезометре, на величину ℎ𝑈 = 𝑈2. 2𝑔 Прибор, объединяющий конструктивно пьезометрическую (П) и коростную (С) трубки, называется прибором (трубкой) Пито ‒ Прандтля и широко применяется для измерения местной скорости движения жидкости: 𝑈 = 2𝑔ℎ𝑈. 1 2 + ℎ  + Для двух сечений потока реальной жидкости уравнение Д. Бернулли имеет вид 𝑧1 + 𝑝1 + 𝛼1 𝑣2 = 𝑧2 + 𝑝2 𝛼2 𝑣2 𝑊, (13) 𝜌𝑔2𝑔 𝜌𝑔 2𝑔 1−2  где 𝛼𝑣22𝑔 скоростной напор, отвечающий средней скорости 𝑣 = 𝑄  𝑆потока жидкости в рассматриваемом живом сечении (здесь Q ‒ расход потока жидкости; S ‒ площадь живого сечения потока); ℎ𝑊1−2 ‒ потеря полного напора (полной удельной энергии) на преодоление работы сил внутреннего и внешнего трения на пути между живыми сечениями потока жидкости I‒I и II‒II; ‒ коэффициент Кориолиса (корректив кинетической энергии), учитывающий неравномерность распределения местных скоростей U по живому сечению потока, обусловленную вязкостью жидкости. Величина зависит от режима течения жидкости и вида движения. Так, при равномерном движении для ламинарного режима = 2,0, а для турбулентного ‒ =1,05…1,15. Слагаемые уравнений (12) и (13) в различных живых сечениях можно изображать графически в виде диаграммы уравнения Д. Бернулли, дающей наглядное представление о перераспределении по пути движения жидкости потенциальной и кинетической энергии, а также о характере убывания полной энергии. |