кцукцк. И. А. Клюева, И. П. Мединцева ПРАКТИКУМ ПО РЕШЕНИЮ ЭКОНОМИЧЕСКИХ. Практикум по решению экономических задач
 Скачать 2.49 Mb. Скачать 2.49 Mb.
|
|
Для решения этой задачи создайте таблицы по образцу. 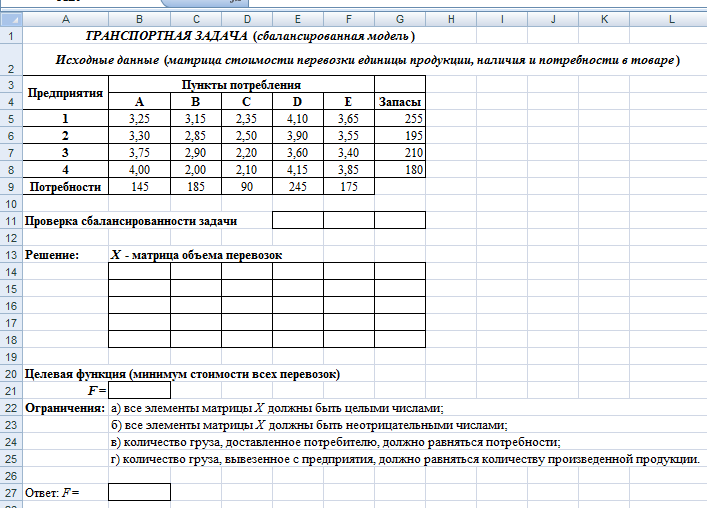 Выполните проверку сбалансированности задачи, для этого в ячейках Е11 и F11 про- суммируйте потребности и запасы (вкладка Формулы категория Математические функция СУММили воспользуйтесь кнопкой Автосуммирование на вкладке Главная). Запишите вывод в ячейке G11 c помощью логической функции ЕСЛИ (вкладка Форму-лы категория Логические): если выполняется условие Е11 = F11, то «Задача является сбалансированной (закрытой)», в противном случае – «Задача является несбалансиро- ванной». В диапазон В14:F17 матрицы Х введите произвольные неотрицательные числа, которые будут представлять собой некоторые предполагаемые объемы перевозок (можно, к примеру, ввести все единицы). Просуммируйте значения данного диапазона по столбцам, введя для этого в ячейку В18 формулу: =СУММ(B14:B17) (вкладка Формулы категория Математические функция СУММ или воспользуйтесь кнопкой Автосуммирование на вкладке Глав-ная). Скопируйте эту формулу в соответствующие ячейки столбцов C, D, E и F с по- мощью маркера автозаполнения. Аналогично просуммируйте значения данного диапазона по строкам, введя для этого в ячейку G14 формулу: =СУММ(B14:F14) (вкладка Формулы категория Математи-ческие или воспользуйтесь кнопкой Автосуммирование на вкладке Главная). Скопи- руйте эту формулу в соответствующие ячейки строк 15, 16 и 17 с помощью маркера ав- тозаполнения. В ячейке В21 вычислите значение целевой функции, подсчитывающей суммарные транспортные расходы на перевозку продукции от поставщиков к потребителям. Целе- вая функция в данной задаче будет равна сумме произведений элементов матрицы та- рифов (стоимости) перевозок В5:F8 и матрицы предполагаемых объемов перевозок В14:F17. Для этого воспользуйтесь функцией СУММПРОИЗВ (вкладка Формулы категория Математические). Полученное значение целевой функции необходимо минимизировать при условии вы- полнения ограничений. Данная задача решается с помощью сервиса MS Excel Поискрешения.  Выделите ячейку В21 и на вкладке Данныевыберите пункт Поискрешения. 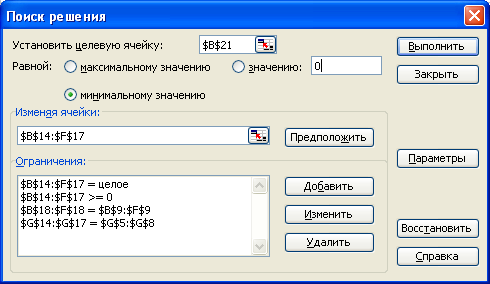 В появившемся диалоговом окне установите необходимые для решения задачи пара- метры. В появившемся диалоговом окне установите необходимые для решения задачи пара- метры.Для создания ограничений задачи нажмите кнопку Добавить, введите необходимые ограничения, записанные в ячейках В22:В25. 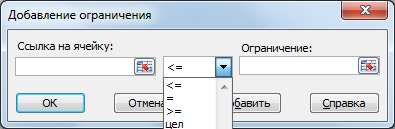 Нажмите кнопку Выполнить. В ячейке В21 у Вас должно получиться значение 2 572,75. При этом обратите внимание на то, как изменились значения матрицы Х– матрицы объемов перевозок. У Вас должно получиться 145 0 90 0 20 Х 0 5 0 35 155 0 0 0 0 180 0 210 0 0 0 Ячейке В27 присвойте полученное значение ячейки В21. На листе Лист2, который назовите Производственная задача (планирование), решите следующую задачу: фирма «ВираМайна» выпускает два типа строительных материалов А и В. Продукция обоих видов поступает в продажу. Для производства материалов ис- пользуются два исходных продукта П1 и П2. Максимально возможные суточные запасы этих продуктов составляют 15 и 19 тонн соответственно. Расходы продуктов П1 и П2 на 1 тонну соответствующих произведенных материалов приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на материал В не превышает спроса на ма- териал А более, чем на 2 т. Кроме того, спрос на материал А никогда не превышает 3 т в сутки. Оптовые цены 1 т материалов обоих видов равны 6 500 у.е. и 5 850 у.е. соответ- ственно. Какое количество материала каждого вида должна выпускать фирма, чтобы доход от реализации был максимальным?
Пусть х1 – суточный объем производства материала А, х2 – суточный объем производ- ства материала Всоответственно. Тогда можем записать целевую функцию F = 6 500х1 + 5 850 х2, вычисляющую при- быль от производства х1 тонн материала А и х2 тонн материала В. Задача состоит в том, чтобы при всех допустимых значениях и существующих ограничениях максимизиро- вать суммарную прибыль от производства материалов. Определим ограничения на переменные: а) объем производства материалов не может быть отрицательным; б) расход исходного продукта для производства обоих видов ма- териалов не может превосходить максимально возможного запаса данного исходного продукта; в) ограничения на величину спроса на материалы. Таким образом, получаем математическую модель задачи: F = 6 500х1 + 5 850 х2 max при следующих ограни- чениях в соответствии с условием задачи: 4,5х1 2,8х2 15, 5,2х 3,5х 19, 1 2 х2 х1 2, х1 3, х1 0, х2 0. Для решения задачи создайте таблицы по образцу:  В ячейки D3 и D4 введите произвольные неотрицательные числа, которые будут пред- ставлять собой некоторые предполагаемые объемы производства материалов обоих ви- дов. В ячейке D7 вычислите значение целевой функции, в диапазон ячеек D9:Е12 введите необходимые ограничения в соответствии с условием задачи. Полученное значение целевой функции необходимо максимизировать при условии вы- полнения ограничений. Для этого выделите ячейку D7 и на вкладке Данные выберите пункт Поиск решения. В появившемся диалоговом окне установите необходимые для решения задачи пара- метры и нажмите кнопку Выполнить. 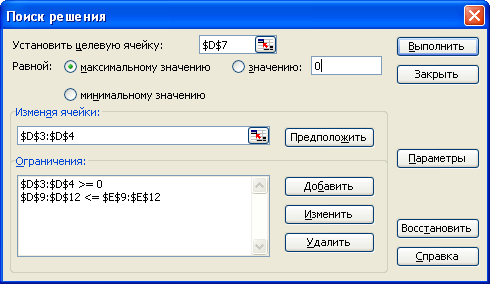 В ячейке D7 должно получиться значение 27 602,74 при выпуске строительных матери- алов Аи Вв объеме 1,29 т и 3,29 т соответственно. Ячейке D14 присвойте полученное значение ячейки D7. Покажите выполненное задание преподавателю. Самостоятельно решите задачи: производство продукции осуществляется на 5-и предприятиях, а затем развозится в 4 пункта потребления. Стоимость перевозки 1 единицы продукции (в у.е.) с предприятий в пункты потребления, объем производства продукции и объемы по- требления приведены в таблице. Необходимо минимизировать суммарные транс- портные расходы по перевозке продукции (F= 1393,1 у.е.);
исходя из специализации и технологических возможностей, предприятие может выпускать четыре вида продукции. Сбыт любого количества продукции обеспе- чен. Для изготовления продукции используются трудовые ресурсы, полуфабрика- ты и станочное оборудование. Общий объем ресурсов (в расчет на трудовую не- делю), расход каждого ресурса на единицу продукции и цена за единицу продук- ции даны в таблице. Определите план выпуска, доставляющий предприятию мак- симальную выручку (F=84 811,1 у.е. при х1=944,44, х2=88,89, х3=0 и х4=144,44).
Покажите выполненное задание преподавателю. ЗА Д А Н И Е 11. ИСПОЛЬЗОВАНИЕ ФИНАНСОВЫХ ФУНКЦИЙ На диске D: в своей папке создайте папку Задание_11, в ней создайте файл MS ExcelЭкономическиерасчеты. Решите следующие задачи: Задача_1. Рассчитайте, какая сумма окажется на счете, если 55 000 руб. вложить в банк на 8 лет под 10,7 % годовых при ежемесячном начислении процентов. Задача_2. Составьте план погашения ссуды, если ссуда размером 1 000 000 руб. выдана сроком на 5 лет под 12,8 % годовых. Задача_3. Рассчитайте размеры ежемесячных / ежегодных выплат для 15-летней ипотечной ссуды размером 3 500 000 руб. по ставке 10,8 % годовых при первона- чальном взносе 25 %. Задача_4. Рассчитайте срок окупаемости некоторого инвестиционного проекта, если инвестиции к началу поступления доходов составят 150 000 000 руб., норма дисконтирования составляет 8,5 %, а ожидаемые ежегодные доходы от реализа- ции проекта составляют 65 000 000 руб. Задача_5. Облигация номиналом 300 000 руб. выпущена на 7 лет. Порядок начис- ления процентов следующий: в первый год – 10,3 %, в следующие три года – 12,4 %, в оставшиеся три года – увеличивается на 0,3 %. Рассчитайте будущую стоимость облигации по процентной ставке сложных годовых процентов. Задача_6. Затраты по инвестиционному проекту составят 500 000 000 руб. Ожида- емые доходы в течение следующих 5 лет составят 50 000 000 руб., 100 000 000 руб., 250 000 000 руб., 200 000 000 руб., 150 000 000 руб. соответственно. Оцените эко- номическую целесообразность проекта по скорости оборота инвестиции, если ры- ночная норма дохода 13,6 %.  Для решения первой задачи на листе Лист1, который переименуйте в Задача_1, запи- шите условие по образцу: Для решения первой задачи на листе Лист1, который переименуйте в Задача_1, запи- шите условие по образцу:Будущая стоимость вклада вычисляется при помощи финансовой функции БС (вкладка Формулы категория Финансовые). При вычислениях учтите, что начисления произ- водятся ежемесячно. Для ежемесячных выплат процентную ставку нужно разделить на 12, а количество периодов соответственно умножить на 12 т.е., в ячейке В8 должна быть записана формула =БС(В4/В5;В6*В5; – В3). 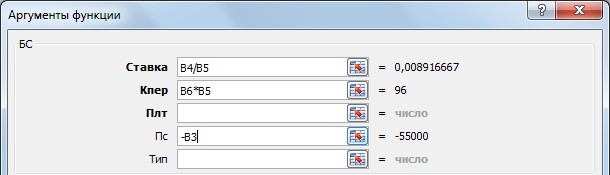 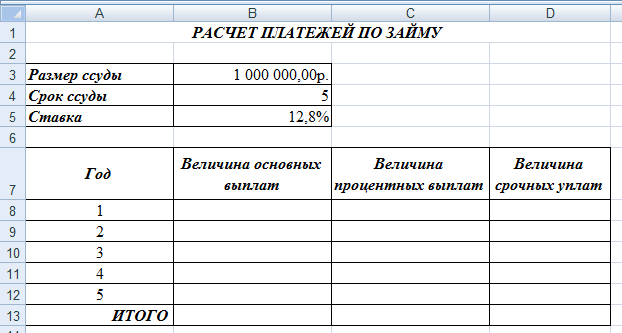 Для решения второй задачи на листе Лист2, который переименуйте в Задача_2, запи- шите условие по образцу: Для решения второй задачи на листе Лист2, который переименуйте в Задача_2, запи- шите условие по образцу:Заполните таблицу с помощью финансовых функций ОСПЛТ,ПРОЦПЛАТ,ПЛТ (вкладка Формулы категория Финансовые). Величина основных выплат = ОСПЛТ($B$5;A8;$B$4;$B$3); 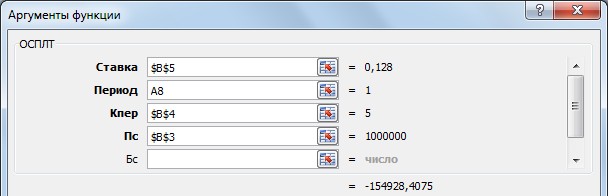 Величина процентных выплат = ПРОЦПЛАТ ($B$5;A8;$B$4;$B$3); 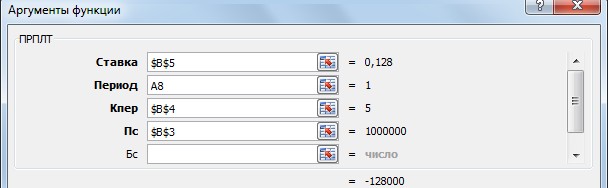 Величина срочных уплат = ПЛТ($B$5;$B$4;$B$3). 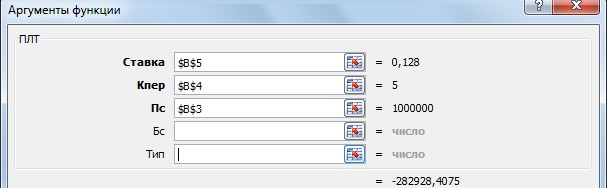 В ячейках В13 (сумма основного долга 1 000 000 руб.), С13 (сумма начисленных за 5 лет процентов) и D13 (сумма всего долга с начисленными процентами) просуммируй- те значения по трем последним столбцам таблицы. Для решения третьей задачи на листе Лист3, который переименуйте в Задача_3, запи- шите условие по образцу: 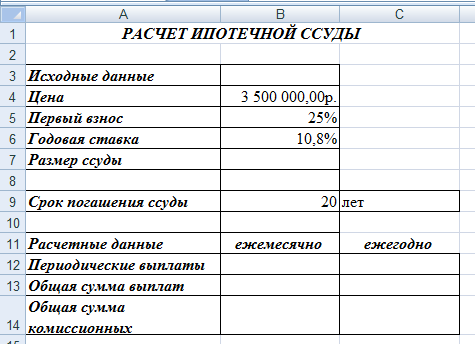 Формулу для вычисления размера ссуды задайте самостоятельно. Заполните расчетные данные: периодические выплаты вычислите с использованием финансовой функции ПЛТ (вкладка Формулы категория Финансовые). Для ежеме- сячных выплат процентную ставку нужно разделить на 12, а количество периодов соот- ветственно умножить на 12. Таким образом, для вычислений надо задать следующие формулы при условии начисления процентов на сумму долга ежемесячно и один раз в год: в ячейке В12 = ПЛТ(В6/12;В9*12;В7), в ячейке С12 = ПЛТ(В6;В9;В7). Для вычислений в остальных ячейках задайте нужные формулы. Добавьте еще 4 листа в рабочую книгу, для этого выполните команды: вкладка Главная Вставить Вставить лист (или щелчком правой кнопки мыши по названию ли- стов вызовите контекстное меню, в котором выберите команду Добавить, после чего активируйте нужный объект). 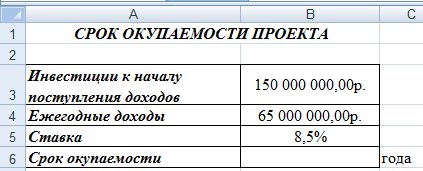 Для решения четвертой задачи на первом добавленном листе Лист4, который переиме- нуйте в Задача_4, запишите условие по образцу: Для решения четвертой задачи на первом добавленном листе Лист4, который переиме- нуйте в Задача_4, запишите условие по образцу:Срок окупаемости инвестиционного проекта вычисляется при помощи финансовой функции КПЕР (вкладка Формулы категория Финансовые). Для данной задачи в ячейке В6 задайте формулу: = КПЕР(В5; В4; – В3). 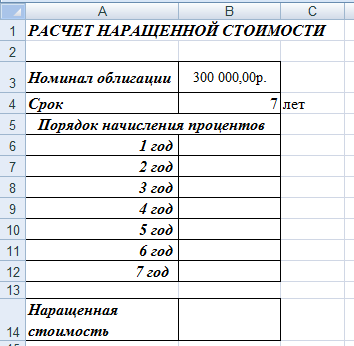 Для решения пятой задачи на втором добавленном листе Лист5, который переименуйте в Задача_5, запишите условие по образцу: Для решения пятой задачи на втором добавленном листе Лист5, который переименуйте в Задача_5, запишите условие по образцу:Значения процентных ставок в ячейки В6:В12 внесите самостоятельно. 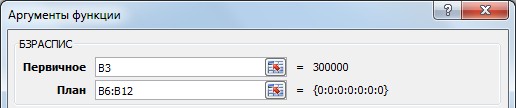 Для расчета будущей стоимости облигации по сложной процентной ставке использует- ся функция БЗРАСПИС (вкладка Формулы категория Финансовые), которая для данной задачи задается в ячейке В14 следующим образом: Для расчета будущей стоимости облигации по сложной процентной ставке использует- ся функция БЗРАСПИС (вкладка Формулы категория Финансовые), которая для данной задачи задается в ячейке В14 следующим образом:Для решения шестой задачи на третьем добавленном листе Лист6, который переиме- нуйте в Задача_6, запишите условие по образцу: 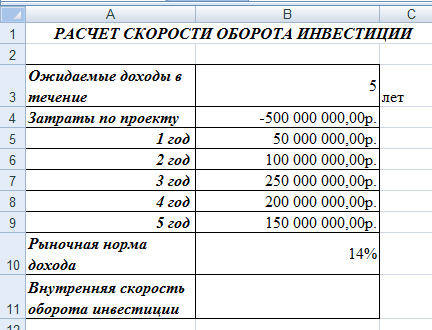 Для расчета нормы доходности по сложной процентной ставке используется функция ВСД (вкладка Формулы категория Финансовые), в которой для данной задачи ис- пользуется только аргумент Значения, один из которых обязательно является отрица- тельным. Если внутренняя скорость оборота инвестиций будет больше рыночной нор- мы доходности, то проект считается экономически целесообразным. В противном слу- чае проект должен быть отвергнут. Для ячейки В11 задайте функцию следующим обра- зом: = ВСД (В4:В9). В ячейке С11 с помощью логической функции ЕСЛИ введите условие, согласно кото- рому в этой ячейке будет выводиться комментарий о целесообразности проекта: если В11 > В10, то «Проект экономически целесообразен», в противном случае «Проект необходимо отвергнуть». Покажите выполненное задание преподавателю. На четвертом добавленном листе, который назовите Самостоятельно, решите следу- ющие задачи (оформите решения по образцам, приведенным выше): Вычислите 7-летнюю ипотечную ссуду для покупки дома стоимостью 10 000 000 руб. с годовой ставкой 8,5 % сложных годовых и первоначальным взносом 15 %. Выполните расчеты для ежеквартальных и ежегодных выплат (вкладка Формулы категория Финансовые функция ПЛТ). Определите, какая сумма окажется на счете, если вклад размером 500 000 руб. размещен на 7 лет под 9,7 % сложных годовых, а проценты начисляются ежеме- сячно (вкладка Формулы категория Финансовые функция БС). Через 4 года фирме «Сатурн-М» понадобится сумма размером 10 000 000 руб. В настоящее время фирма готова положить некоторую сумму единым вкладом на депозит под 12,8 % сложных годовых. Проценты будут начисляться ежекварталь- но. Определите сумму начального вклада. (вкладка Формулы категория Финан-совые функция ПС). Сколько потребуется лет, чтобы вклад размером 400 000 руб. достиг значения 1 000 000 руб., если ставка сложных годовых процентов 13,5 % и проценты начисляются каждые два месяца? (вкладка Формулы категория Финансовые функция КПЕР). Рассчитайте будущую стоимость облигации номиналом 100 000 руб., выпущен- ной на 5 лет, если первые два года проценты начисляются по ставке 16 % слож- ных годовых, а в течение следующих трех лет процентная ставка ежегодно увели- чивается на 0,4 %. (вкладка Формулы категория Финансовые функция БЗРАСПИС). Затраты по проекту составят 1 000 000 000 руб. Ожидаемые доходы в течение по- следующих 5 лет составят соответственно 350 000 000 руб., 250 000 000 руб., 250 000 000 руб., 400 000 000 руб., 300 000 000 руб. Оцените экономическую це- лесообразность проекта по скорости оборота инвестиции, если рыночная норма дохода 12 %. (вкладка Формулы категория Финансовые функция ВСД). Покажите выполненное задание преподавателю. ЗА Д А Н И Е 12. ФУНКЦИИ ПРОСМОТРА ССЫЛОК И МАССИВОВ На диске D: в своей папке создайте папку Задание_12, в ней создайте файл MSExcelВедомость. 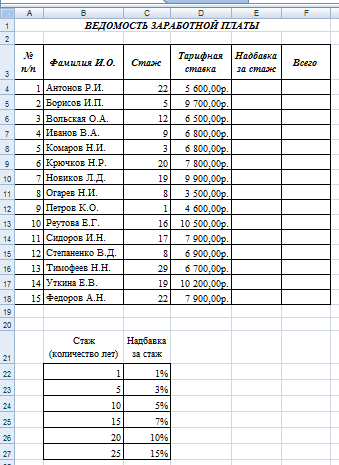 На листе Лист1, который назовите Ведомостьзарплаты, создайте основную и вспомо- гательную таблицы по следующему образцу: На листе Лист1, который назовите Ведомостьзарплаты, создайте основную и вспомо- гательную таблицы по следующему образцу:Заполните таблицу, для этого в ячейку Е4 введите формулу: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
