Практикум по решению задач 1. Тема 2 Метод критического пути Задача 1 Руководитель проекта разработал следующий перечень работ
 Скачать 296.38 Kb. Скачать 296.38 Kb.
|
|
Практикум по решению задач №1. Тема № 2 «Метод критического пути» Задача 1 Руководитель проекта разработал следующий перечень работ:
Вопросы: Какова длина критического пути? Сколько работ находится на критическом пути? Можно ли отложить выполнение работы F без отсрочки завершения проекта в целом? Задача 2 Проект пусконаладки компьютерной системы состоит из восьми работ. Непосредственно предшествующие работы и продолжительность выполнения работ показаны ниже.
Вопросы: Сколько времени потребуется для выполнения проекта? Сколько работ на критическом пути? Чему равно наиболее раннее время начала работы C? Решение. Найдем критический путь при нормальном времени выполнения работ. Используем для этого метод СРМ. Вводим в программу POMWIN исходную информацию, описывающую проект в виде последовательности работ: 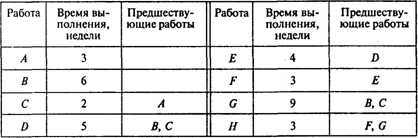 Выполнив расчеты, получаем следующие результаты: 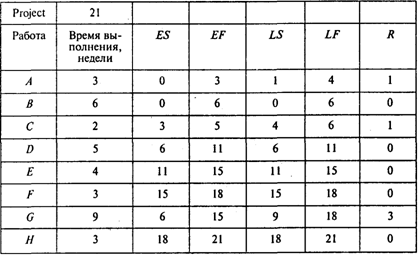 Отсюда видно, что при нормальной продолжительности работ длина критического пути составляет 21 неделю. На критическом пути находятся работы В, D, Е, F, Н. Для того чтобы определить затраты на выполнение проекта при нормальной продолжительности работ, достаточно просуммировать затраты, указанные в пятом столбце таблицы исходных данных. В результате получаем затраты 18 700 руб. Для определения минимальных дополнительных издержек, необходимых для того, чтобы снизить продолжительность проекта до 16 недель, построим модель линейного программирования. Для этого на основании данных о непосредственно предшествующих работах построим графическое представление проекта (рис. 1). 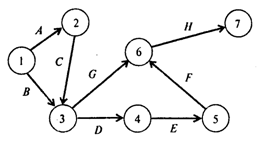 Рис. 1 Используя исходные данные, определяем удельные (в единицу времени) затраты КIj на сокращение продолжительности работ. Получаем следующие результаты: 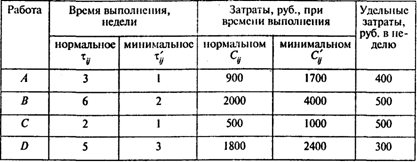 Окончание таблицы 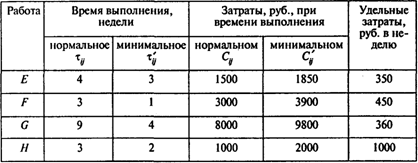 Используя обозначения ХI — время наступления события I, УIj — величина сокращения времени работы (I,J), получаем следующую модель линейного программирования для определения минимальных издержек, необходимых для сокращения продолжительности проекта с 21 до 16 недель: При условиях 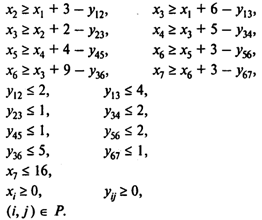 Для решения этой задачи линейного программирования используем программу POMWIN. В следующей таблице приведенная выше модель представлена в формате программы POMWIN: 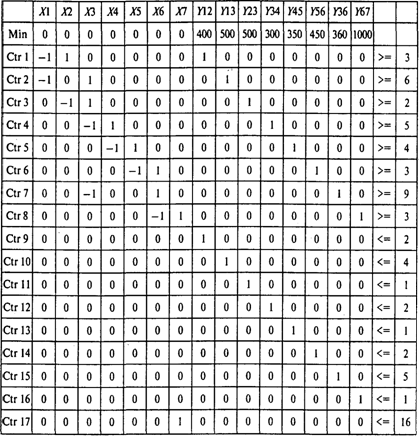 Выполнив расчеты, получаем следующие результаты: 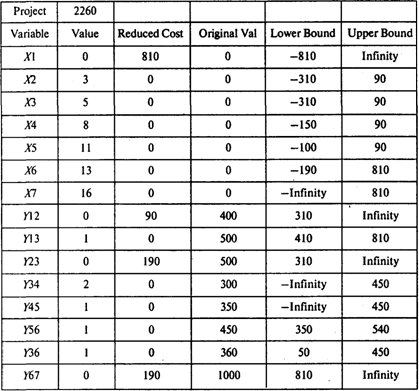 Итак, минимальные затраты, необходимые для того, чтобы сократить продолжительность проекта с 21 до 16 недель, составляют 2260 руб. Продолжительность каждой из работ (1, 3), (4, 5), (5, 6) и (3, 6) сокращается на одну неделю. Продолжительность работы (3, 4) сокращается на две недели. Ответы: 1. 21 неделя. 2. Пять работ. 3. 18 700 руб. 4. 2260 руб. Задача 3
Рассмотрите следующую сеть проекта (продолжительность работ показана в неделях) Вопросы За какое минимальное время может быть выполнен проект? Сколько работ находится на критическом пути? На сколько недель можно отложить выполнение работы D без отсрочки завершения проекта в целом? Строим сетевой график: 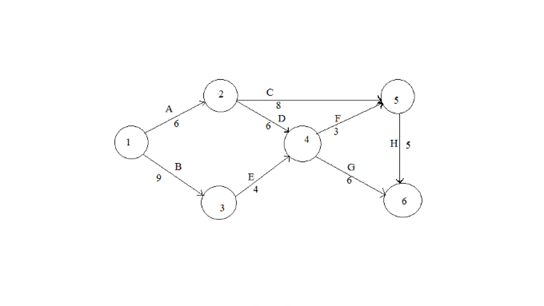 Рисунок 1 Модель сетевого графика Решение: Этап 1. При вычислении tp( i) перемещаемся по сетевому графику от исходного события 1 к завершающему событию 6. tp(1)= 0. В событие 2 входит только одна работа: tp(2)= tp(1)+ tp(1,2)= 0 + 6 = 6. Аналогично tp(3)= tp(2)+ tp(1,3)= 0 + 9 = 9. В событие 4 входит две работы: tp(4) = max ( tp(2) + t (2,4),tp(3) + t(3,4)) = max (6+6,3+4) = 12. tp(5) = max ( tp(2) + t (2,5), tp(4) + t(4,5)) = max (6+8,12+3) = 15. tp(6) = max ( tp(4) + t (4,6), tp(5) + t(5,6)) = max (12+6,15+5) = 20. Следовательно, критический путь равен 20 недель. Этап 2. При вычислении tn(i) перемещаемся от завершающего события 6 к исходному событию 1 по сетевому графику против стрелок. tn(6) = tp(6) = 20. Далее рассмотрим непосредственно предшествующее событие 5, из которого выходит только одна работа (5,6): tn(5)=tn(6) -t(5,6) = 20-5 = 15. Из события 4 выходят две работы: (4,5) и (4,6). Поэтому определяем tn(4) по каждой из этих работ: tn(4) = min(tn(5) -t (4,5), tn(6) -t(4,6)) = min (15-3,20-6) = 12. tn(3) = tn(4) -t(3,4)= 12-4 = 8. tn(2) = min(tn(5) -t (2,5), tn(4) -t(2,4)) = min (15-8,12-6) = 6. tn(1) = min(tn(2) -t (1,2), tn(3) -t(1,3)) = min (6-6,8-9) = 0. Этап3. Вычисляем R(i) = tn(i) -tp(i) резерв времени события i, то есть из чисел, полученных на этапе 2, вычисляем числа, полученные на этапе 1. R(1) =0 -0 = 0. R(2) = 6 -6 = 0. R(3) = 8-3 = 5. R(4) = 12 -12 = 0. R(5) = 15 -15 = 0. R(6) = 20 -20 = 0. Этап 4. У критических событий резерв времени равен нулю, так как ранние и поздние сроки их свершения совпадают. Критические события 2,3,4,5,6 и определяют критический путь. Для завершения проекта потребуется 20 недели. Работа D = (2,4) расположена на критическом пути. Поэтому ее отложить без отсрочки завершения проекта в целом. Работа C = (2,5) не расположена на критическом пути, ее можно задержать на tn(5) - tp(2) - t(2,5) = 15-6-8 = 1 неделю Задача 4
Экономический факультет МГУ разрабатывает новую программу повышения квалификации преподавателей количественных методов анализа экономики. Желательно, чтобы эту программу можно было реализовать в наиболее сжатые сроки. Существуют взаимосвязи между дисциплинами, которые необходимо отразить, составляя расписание занятий по программе. Например, сетевые методы планирования должны рассматриваться лишь после того, как слушатели обсудят различные аспекты (коммерческие, финансовые, экономические, технические и т.д.) проектного анализа, связанные с жизненным циклом проекта. Дисциплины и их взаимосвязь указаны в следующей таблице. Вопросы: Найдите минимальное время, за которое можно выполнить программу. Какое количество дисциплин находится на критическом пути? Каков резерв времени изучения дисциплины F? |
