Урок финансовой грамотности для старшеклассников. Практикум по теме "Использование процентов в финансовых расчетах" Разработала учитель математики мбоу Лицей 35 г. Майкопа Республики Адыгея Шепталенко Татьяна Николаевна
 Скачать 51.39 Kb. Скачать 51.39 Kb.
|
|
Урок-практикум по теме: "Использование процентов в финансовых расчетах" Разработала: учитель математики МБОУ «Лицей №35» г. Майкопа Республики Адыгея Шепталенко Татьяна Николаевна Цели урока: Формировать финансовую грамотность учащихся; Повторить и закрепить знания о процентах, Развивать навыки применения формул для удобства анализа и принятия решений; Показать прикладную направленность математики на примере использования процентов в финансовых расчетах. Ход урока: 1. О/м 2. Постановка целей и задач урока. День финансиста- праздник российского финансового сообщества, установленный Указом Президента Российской Федерации Медведева Д.А. от 19 августа 2011 года, как новый официальный государственный профессиональный праздник; отмечается ежегодно 8 сентября - в этот день, в 1802 году Император Александр I своим Высочайшим Манифестом основал Министерство финансов России. Кто же такие финансисты? (Финансист - это специалист по финансовым (денежным) операциям.) Он из кризиса выводит, В банке он счета заводит. Знает, деньги как копить, Как дефолт предотвратить. Все подсчеты производит, Инвестиции проводит, Не пропустит ни рубля, Риски сводит до нуля. Мы присоединяемся к поздравлениям, которые прозвучат сегодня в адрес финансистов и приурочим урок математики к этому событию. А заодно, повторим и обобщим знания о процентах, их использовании в финансовых расчетах. Рассмотрим различные условия хранения вкладов и проанализируем выгоду. 3. Актуализация знаний. В экономических и статистических расчетах, а также во многих отраслях науки части величин принято выражать в процентах (сотых долях). Это имеет свои практические удобства, ибо выражение частей чисел в одних и тех же (сотых) долях позволяет: быстро сравнивать величины частей числа со всем числом и между собой, упростить расчеты и в то же время добиться достаточной степени точности выражения частей величин целыми числами (в тех случаях, когда измерение в десятых долях было бы слишком грубым, а в тысячных – излишне точным). Наиболее часто проценты применяются при финансовых расчетах (банковское дело, доходы от облигаций госзаймов, вкладов в сберегательные банки и т.п.), а также при учете роста хозяйственной продукции, выполнения производственных планов, роста народонаселения и т.д. Что же такое "процент"? (сотая часть числа). Финансисты различают простые и сложные проценты. При финансовых расчетах число, показывающее, сколько процентов дохода в установленный срок (зачастую в год) приносит та или иная сумма, называется процентной таксой (ставкой), а сама сумма дохода – процентными деньгами. Для расчета процентных денег служат формулы простых и сложных процентов. Если проценты начисляются по отношению к исходной сумме, то такой метод называется методом простых процентов. Если проценты начисляются по отношению к величине, включающей первоначальную сумму и проценты, начисленные за прошедший период, то такой метод называется методом сложных процентов. Обозначим: В – первоначальная сумма вклада; t – период начисления процентов – время, по истечении которого начисляются процентные деньги; р – ставка простого процента – доля вклада, которая начисляется вкладчику по истечению периода t; Р – процентные деньги за весь срок использования вклада; Т – срок использования вклада (банком); n = Т / t – количество периодов начисления процентов за срок использования вклада; S – сумма, образовавшаяся на вкладе к концу срока Т, тогда Sn= B(1+ np) – начисление по формуле простых % Sn= B(1+ p)n начисление по формуле сложных % Ваша задача выполнить расчеты по данным формулам. Заполнить таблицы, построить графики наращивания процентных денег и проанализировать свою выгоду. 4. Выполнение практических заданий. Описание см. Практические работы №1, 2. 5. Подведение итогов: Сравнивая полученные результаты расчетов, мы сделали вывод, что 1. самым прибыльным является условие хранения с ежемесячным начислением процентов. 2. Вкладчику выгодно размещать в банке деньги на условиях сложных процентов. Кроме того, отметим, что механизм начисления процентов по банковским кредитам аналогичен. И если вы когда-нибудь решите оформить кредит, то правильно оцените все риски и сможете подсчитать сумму возврата долга по процентам. 6. Д/з: Ознакомиться, на каких условиях Сбербанк предлагает Потребительский кредит, подсчитать выплаты по процентам, если сумма кредита 100000 руб, срок на 1 год. Практическая работа №1 "Расчёт процента от суммы банковского вклада" Цели: изучить понятия "простые проценты" и "сложные проценты"; научиться решать задачи на проценты и банковские расчёты, анализировать, осмысливать и извлекать необходимую информацию для принятия решений. Задача 1. В сбербанке установлены следующие процентные ставки: 1) 2 % от суммы вклада с ежемесячной выплатой дохода; 2) 6 % от суммы вклада при условии его хранения в течение трех месяцев (депозит на три месяца); 3) 12,5 % от суммы вклада при условии его хранения в течение шести месяцев (депозит на полгода); 4) 25 % годовых при условии хранения вклада в течение года. При каком условии хранения процентные деньги окажутся наибольшими, если вкладчик не будет их изымать в течение года? Ход работы: Из условия задачи следует, что имеют место сложные проценты, поэтому экономико-математическая модель данной задачи выражается одной и той же формулой 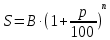 где р принимает соответственно значения: 2; 6; 12,5; 25. Число n в первом случае равно 12, так как после каждого месяца (в течение года) производится перерасчет, во втором случае n = 4, в третьем n = 2, а в четвертом n = 1. Обозначим S1, S2, S3, S4 – суммы вклада после 1-го года хранения на условиях 1), 2), 3), 4) соответственно. Тогда S1=… S2=… S3=….. S4=…. Занесем полученные результаты в таблицу:
Выводы: Сравнивая полученные числа, видим, что наибольшим является ____________, поэтому самым прибыльным является условие хранения ___________________ Практическая работа №2 "Сравнение роста процентных денег на условиях простых и сложных процентов " Задача 2. Некто планирует разместить в банке вклад в 10 000 руб. на длительный срок. Процентная ставка в банке – 10% годовых. Необходимо проанализировать возможный рост процентных денег на условиях простых и сложных процентов. Ход работы: Имеем В = 10 000, р = 10 % (или 0,1). Результаты расчетов представим следующей таблицей.
Для большей наглядности представим на графике процесс наращивания процентных денег (данные таблицы за вычетом первоначальной суммы 10 000 руб.) при простых и сложных процентах. - - - -простые проценты;  сложные проценты сложные проценты  Из таблицы и графиков видно, что различие процентных денег при простых и сложных процентах с течением времени (с увеличением количества периодов начисления процентов) становится все более ощутимым и, если через 10 лет на простых процентах вклад удвоится, то на сложных увеличится почти в 2,6 раза Вывод: Вкладчику выгодно размещать в банке деньги на условиях __________ ___________процентов. |
