Комбинаторика. Правила сложения и умножения в комбинаторике
 Скачать 182.15 Kb. Скачать 182.15 Kb.
|
|
Правила сложения и умножения в комбинаторике Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами. Пример 1. В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного? Решение Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек. По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами. Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены: способами. Пример 2. В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных? Решение Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами. После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами. По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами. Сочетания без повторений. Сочетания с повторениями Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькимиспособамиможновыбратьm изn различных предметов? Пример 3. Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать? Решение Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4: Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькимиспособамиможновыбратьm ( Пример 4. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных? Решение Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4. Размещения без повторений. Размещения с повторениями Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом:сколькимиспособамиможновыбратьиразместитьпоm различнымместамm изn различныхпредметов? Пример 5. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии? Решение. В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента: Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами. Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом:сколькимиспособамиможновыбратьиразместитьпоm различнымместамm изn предметов, средикоторыхестьодинаковые? Пример 6. У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик? Решение Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5: Перестановки без повторений. Перестановки с повторениями Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькимиспособамиможноразместитьnразличныхпредметовнаn различныхместах? Пример 7. Сколько можно составить четырехбуквенных «слов» из букв слова«брак»? Решение Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е. Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы. 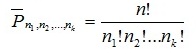 Пример 8. Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»? Решение Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ "КОМБИНАТОРИКА" 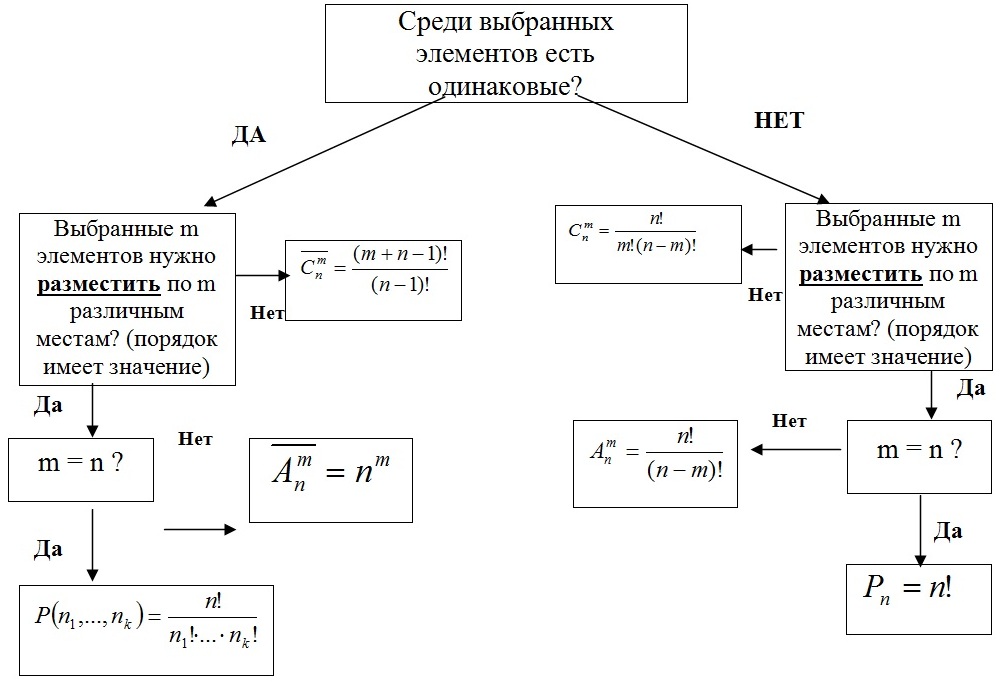 Сколько существует чисел, делящихся на 5, десятичная запись которых содержит 5 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, делящихся на 5, десятичная запись которых содержит 6 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, делящихся на 5, десятичная запись которых содержит 7 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, делящихся на 5, десятичная запись которых содержит 8 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, восьмеричная запись которых содержит 5 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, восьмеричная запись которых содержит 6 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, восьмеричная запись которых содержит 7 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, восьмеричная запись которых содержит 8 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, шестнадцатеричная запись которых содержит 3 цифры, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, шестнадцатеричная запись которых содержит 4 цифры, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Сколько существует чисел, шестнадцатеричная запись которых содержит 5 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом. Ваня Сергей составляет 6-буквенные коды из букв К, Л, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей? Сергей составляет 5-буквенные коды из букв С, Е, Р, Г, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей? Сергей составляет 5-буквенные коды из букв Ж, А, Л, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей? Сергей составляет 5-буквенные коды из букв В, О, Р, О, Б, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей? Сергей составляет 6-буквенные коды из букв С, О, Л, О, В, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей? Начнем с того, что у нас вопрос, о том сколько различных кодов и поэтому будем считать 2 буквы О за одну. 1) нет Й- 5^6=15625 2) Й на втором месте : 4*1*4*5*5*5= 3) Й на третьем месте: 5*4*1*4*5*5 4) Й на четвертом месте: 5*5*4*1*4*5 5) Й на пятом месте: 5*5*5*4*1*4 Всего с Й: 4^3*5^3=20^3=8000 Итого ответ: 15625+8000=23625 Сергей составляет 6-буквенные коды из букв Е, Л, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей? Сергей составляет 6-буквенные коды из букв К, А, Л, И, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой И. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей?
Василий составляет 4-буквенные коды из букв Б, Е, Р, К, Л, И, Й. Каждую букву можно использовать любое количество раз, при этом код не может начинаться с буквы Й и должен содержать хотя бы одну гласную. Сколько различных кодов может составить Василий? Василий составляет 4-буквенные коды из букв В, А, Я, Ю, Щ, И, Й. Каждую букву можно использовать любое количество раз, при этом код не может начинаться с буквы Й и должен содержать хотя бы одну гласную. Сколько различных кодов может составить Василий? Из букв слова Р У С Т А М составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных? Из букв А З И М У Т составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных? Из букв слова Р А Д У Г А составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных? Из букв слова Р А З М А Х составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных? Из букв слова К О Р Т И К составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных? Из букв слова К А Р К А С составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных? Из букв слова К А Н К А Н составляются 6-буквенные последовательности. Сколько можно составить различных последовательностей, если известно, что в каждой из них содержится не менее 3 согласных?
|
