математика вариант 8. математика. Правила сложения и умножения вероятностей
 Скачать 23.33 Kb.
|
|
Тема 1. Элементы комбинаторики. События и их вероятности, классический и геометрический способы подсчета вероятностей Вариант 8. На складе имеется 15 телевизоров, причем 10 из них изготовлены отечественным производителем. Найти вероятность того, что среди пяти взятых наудачу телевизоров окажутся три отечественных телевизора. P(A)=m/n m-количество благоприятных исходов n-количество всех исходов А-три телевизора отечественных среди пяти отобранных    Ответ: 0,4 Тема 2.Операции над событиями. Правила сложения и умножения вероятностей Вариант 8. Брошены три игральные кости. Найти вероятность того, что на каждой из выпавших граней появится пять очков. Пусть событие A - на каждой грани появилось 5 очков. Вероятность выпадения пятёрки при одном броске: 1/6. броски - независимые события, поэтому вероятность, что 5 выпадет на всех гранях равна: P(A) = 1/6 · 1/6 · 1/6 = 1/216 = 0,0046. Ответ: 0,0046 Тема 3. Формула полной вероятности. Формулы Бейеса Вариант 8. Страховая компания разделяет водителей по трём классам: № 1 (мало рискует), № 2 (рискует средне), № 3 (рискует сильно). Компания предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат классу № 1, 50% - к классу № 2 и 20% - к классу № 3. Вероятность того, что в течение года водитель класса № 1 попадает в одну аварию, равна 0,01, для водителя класса № 2 эта вероятность равна 0,02, а для класса № 3 – 0,08. Найти вероятность того, что водитель, застраховавший свою машину, попадает в аварию в течение года. По формуле полной вероятности имеем следующее: Р(А) = 0,01 * 0,3 + 0,02 * 0,5 + 0,08 * 0,2 = 0,003 + 0,01 + 0,016 = 0,029 — это вероятность того, что случайный застрахованный водитель попадёт в аварию. Ответ: 0,029 Тема 4. Повторение независимых испытаний. Наивероятнейшее число успехов. Формулы Бернулли, Лапласа, Пуассона. Вариант 8. Известно, что в большой партии радиоламп 90% стандартных. Найти вероятности того, что из 300 отобранных радиоламп стандартных окажутся: а) ровно 270; б) от 260 до 275; в) не менее 275. Число испытаний n= 300 велико; вероятность p= 0,9 появления события A немала; q= 1 - p= 0,1; npq= 300*0,9*0,1 = 27  20, поэтому воспользуемся локальной и интегральной формулами Лапласа.а) Имеем: n=300, p=0,9, q=0,1, k=270, np=270, npq=27, 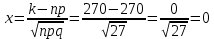 . По таблице 1 приложения  . По локальной приближенной формуле Лапласа  получим .б) Имеем: n=300, p=0,9, q=0,1, k1=260, k2 =275, np=270,  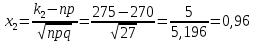=5,196,  ,  . Функция 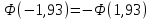 нечетная, поэтому  . По таблице 2 приложения находим  ,  . По интегральной приближенной формуле Лапласа  имеем   .в) Имеем: n=300, p=0,9, q=0,1, k1=275, k2 = 300, np=270, =5,196,  ,  . По таблице 2 приложения находим  . По интегральной приближенной формуле Лапласа имеем  .Ответ: 0,0268 |