Вычитание
Из теории множеств известно, что разность множеств А и В, если В – подмножество А, называется дополнением множества В до множества А.
Мы можем изобразить дополнение одного множества до другого, число элементов дополнения можно найти счетом. Кроме того, в теории множеств доказано, что число элементов дополнения множества В до множества А равно разности числа элементов множества А и множества В.
К р а т к а я з а п и с ь : m(BA) = m(A) – m(B) (1), если B ⊂ A.
Пусть a = m(A), b = m(B), где a, b ∈ No.
Сделав замену в равенстве (1), получим предложение a – b == m(BA), из которого можно сформулировать определение разности чисел a и b.
Определение 8. Разностью целых неотрицательных чисел а и b называется число элементов дополнения множества В до множества А, если a = m(А), b = m(В) и В ⊂ А.
К р а т к а я з а п и с ь : a – b = m(ВА), где m(А) = a, m(В) = b, В⊂А .
З а д а н и е 4. Найдите значение разности: а) 8 и 5, б) 5 и 0. Докажите, что 7 – 5 = 2.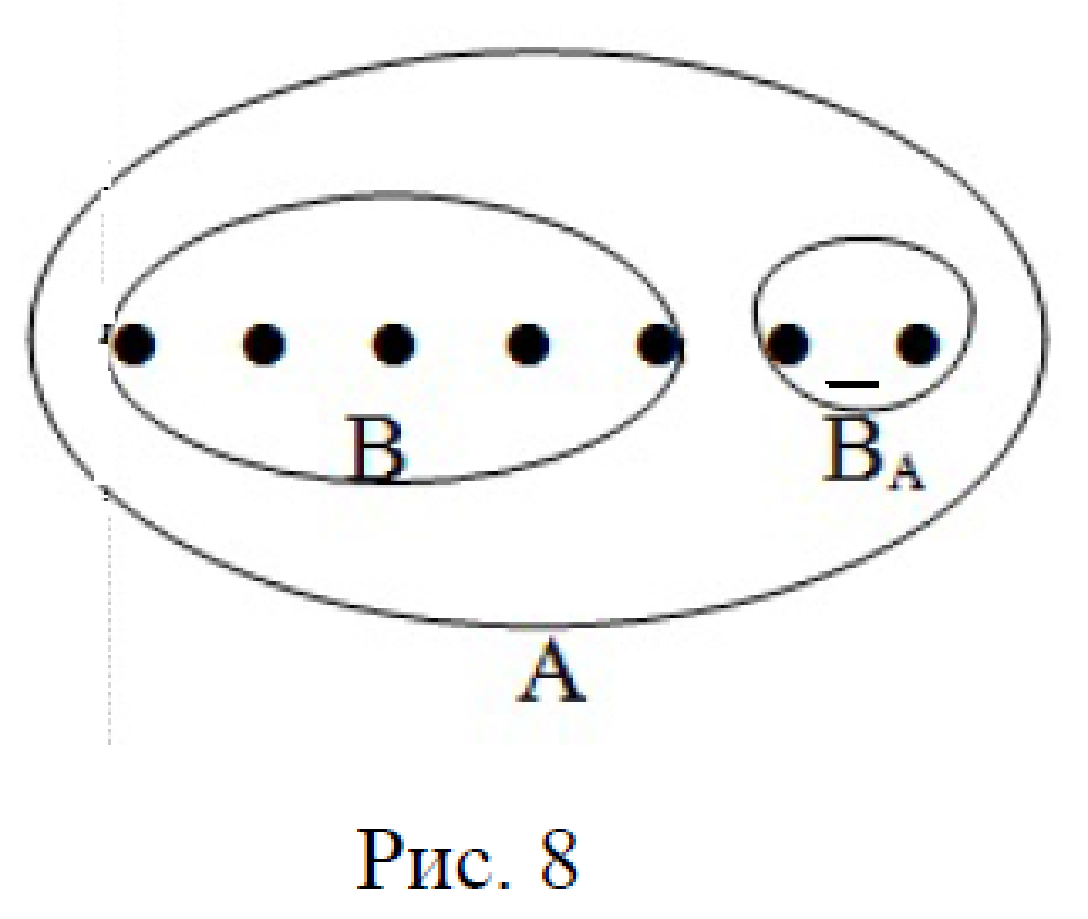
При этом:
а) см. задачу на нахождение суммы чисел (с. 9);
б) используйте А \ Ø = А, m(A \ Ø) = m(A), A \ Ø = ØA.
Решение.
1) По определению разности 7 – 5 = m(ВА) (1), где 7 = m(А), 5 = m(В) и В ⊂ А. Известно, что разность равна 2. Значит, нужно доказать, что m(ВА) = 2.
2) Изобразим множества А и В (рис. 8), где B ⊂ A.
Элементы из множества А, не вошедшие в множество В, образуют третье множество – дополнение множества В до А, т.е. ВА. Используя счет предметов, получим ВА
N2, т.е. m(ВА) = 2 (2).
Из (1) и (2) следует, что 7 – 5 = 2 – верное равенство.
Из определения разности чисел a и b мы видим связь вычитания чисел с разностью множеств, из которых второе будет подмножеством первого, т.е. с дополнением второго множества до первого.
Справедливо и обратное. Связь дополнения множеств со сложением чисел раскроем при решении текстовых задач.
В школе дети учатся решать задачи на вычитание четырех типов:
• на нахождение остатка;
• на нахождение неизвестного слагаемого по сумме и известному слагаемому;
• на разностное сравнение;
• на уменьшение на число (в прямой и косвенной форме).
З а д а н и е 5. Обосновать выбор действия и ответить на вопрос.
Задача 1. Катя сорвала 12 ромашек, три ромашки она отдала Маше. Сколько ромашек осталось у Кати?
1. Работа с условием.
Пусть А – множество ромашек, которые сорвала Катя, m(А) = 12;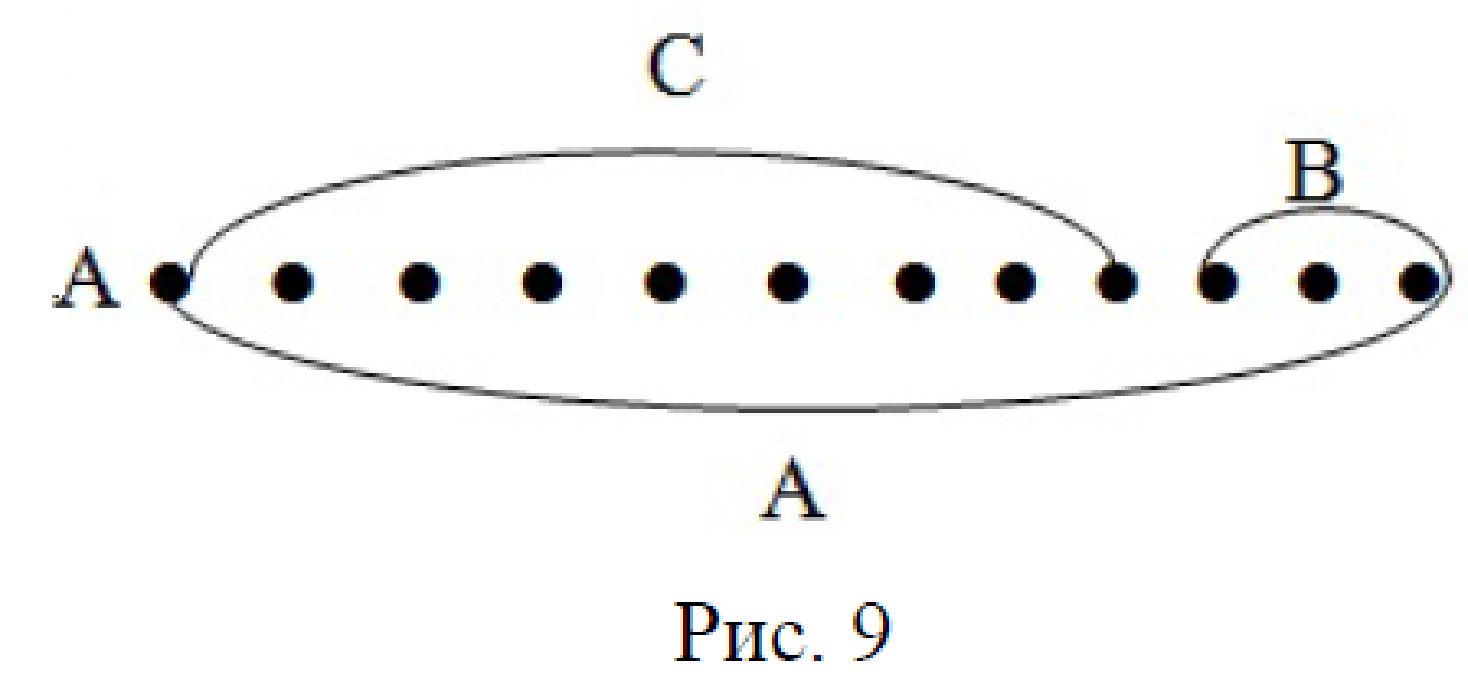
В – множество ромашек, которые Катя отдала, m(В) = 3;
С – множество ромашек, которые остались у Кати, m(С) = ?
2. Изобразим множество С (построим модель к задаче) на рис. 9.
Для этого можно изобразить:
1) А, m(А) = 12 (элементы А – точки);
2) В, m(В) = 3 и В⊂ А;
3) элементы из А, которые не принадлежат множеству В, образуют множество С. По определению, С = А\ В и так как В ⊂ А, то C = ВА.
3. Нужно найти m(С), где множество С равно дополнению множества В до множества А, значит, задачу нужно решать вычитанием. Обоснование можно провести иначе.
Для нахождения m(С), используем теорему о числе элементов дополнения к подмножеству, получим m(С) = m(А) – m(В), сделаем замену m(С) = 12 – 3. В этом случае мы не только доказали, что задачу решаем вычитанием, но и составили выражение, значение которого нужно найти.
4. Чтобы ответить на вопрос задачи, найдем m(С) счетом. Получим С
N9 => m(С) = m(N9), m(С) = 9, т.е. у Кати осталось 9 ромашек.
Вывод. 1. Доказали, что задачу нужно решать вычитанием.
2. Ответили на вопрос задачи.
Задача 2. В букете всего 12 ромашек и васильков. Сколько ромашек в букете, если в нем 7 васильков? 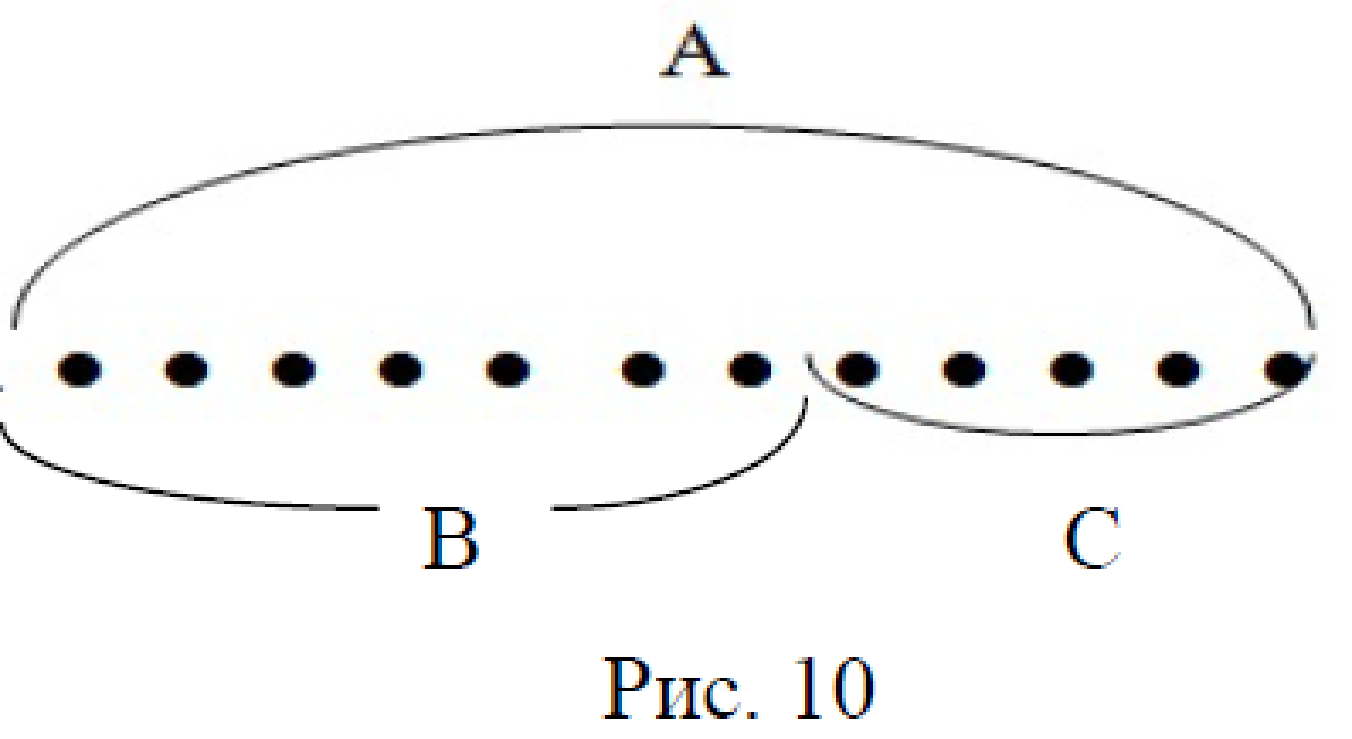
1. Работа с условием.
Пусть А – множество цветков в букете, m(А) = 12;
В – множество васильков в букете, m(В) = 7;
С – множество ромашек в букете, m(С) = ?
2. Модель к задаче (рис. 10).
Можно изобразить:
1) А, m(А) = 12;
2) В, m(В) = 7, В ⊂ А;
3) Существует С, С = А\ В, и так как В⊂А, то C = В-А .
3. См. объяснение в задаче 1 и дополнить решение,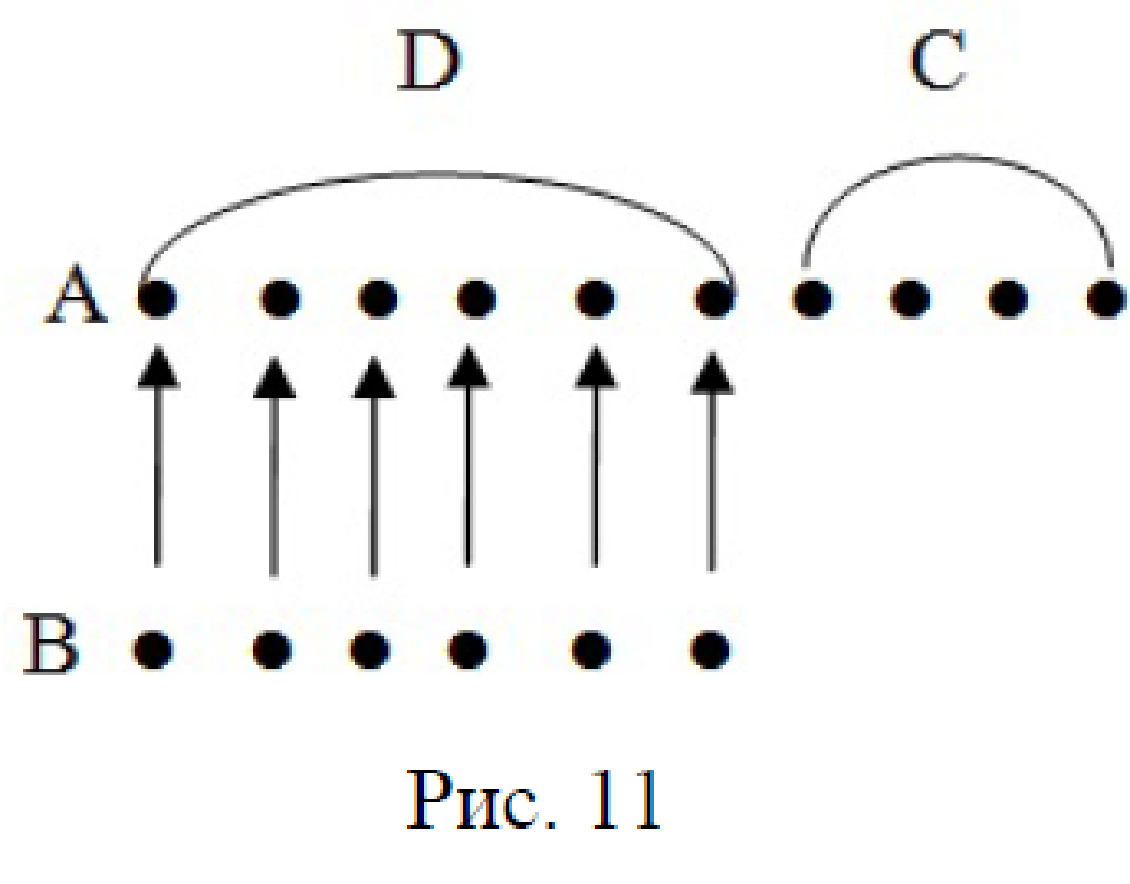
4. См. объяснение в задаче 2 и дополнить решение.
Задача 3. В букете 10 ромашек и 6 васильков. На сколько васильков меньше, чем ромашек?
1. Работа с условием.
Пусть А – множество ромашек, m(А) = 10,
В – множество васильков, m(В) = 6,
С – множество цветов, где m(С) показывает, насколько число васильков меньше числа ромашек. Найти m(С).
2. Изобразим множество С (построим модель к задаче) на рис. 11.
Изобразим:
1) А, m(А) = 10;
2) В, m(В) = 6.
Число ромашек больше числа васильков на какое-то число х. По определению «больше на число х», ромашек столько, сколько васильков да еще x штук. Поэтому множество А будет разбито на два подмножества D и С, где D
В и m(С) = х.
3. Нужно найти m(С), С = А\ D и D⊂А, значит, С = DА. Задачу нужно решать вычитанием, а именно, т.к. m(С) = m(DА) и m(DА) = m(А) – m(D) и m(D) = m(В), тогда получаем, что m(С) = 10 – 6.
4. Чтобы ответить на вопрос задачи, найдем m (C). С
(N4), m(C) = 4. Васильков на 4 меньше, чем ромашек.
Задача 4. В букете 12 ромашек, а васильков на 5 меньше, чем ромашек. Сколько васильков в букете?
1. Работа с условием.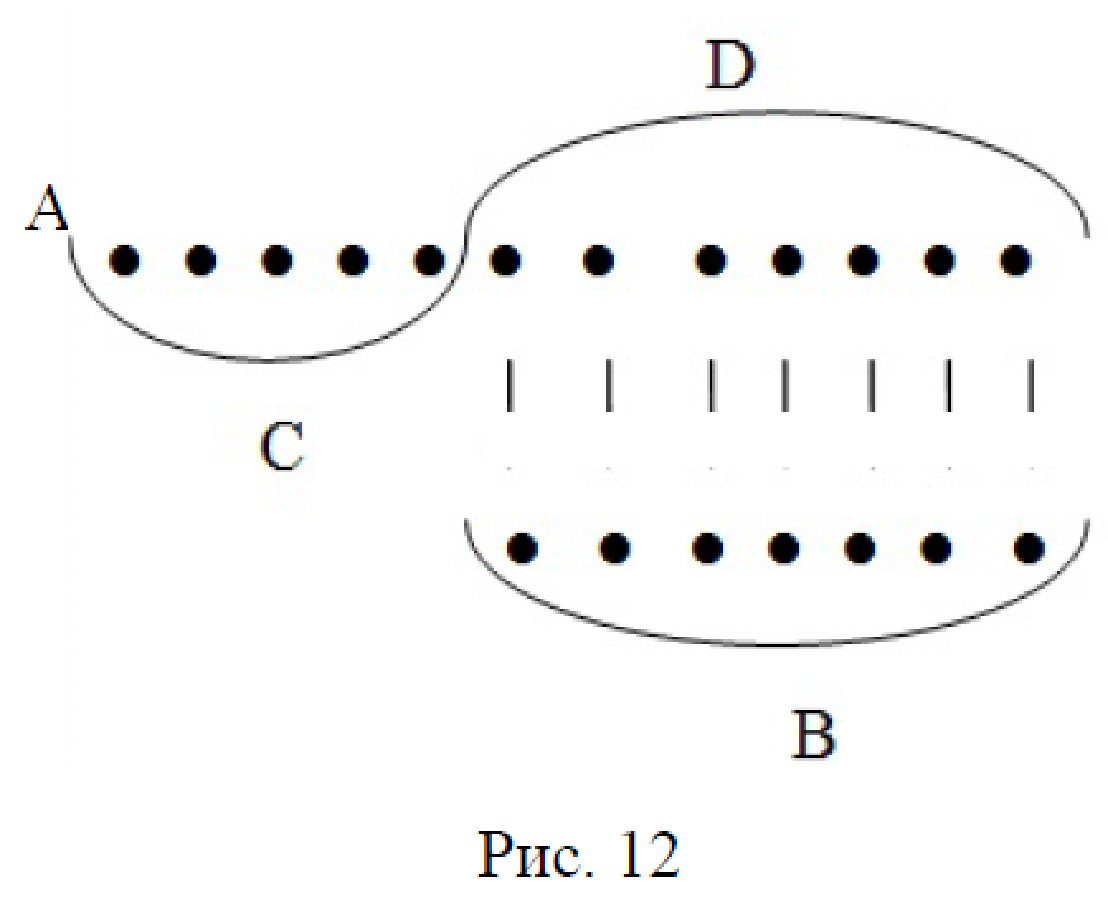
Пусть А – множество ромашек, m(А) = 12,
В – множество васильков, m(В) = ?
С – множество цветков, m(С) = 5.
5 – показывает, на сколько число васильков меньше числа ромашек.
2. Изобразим множество В. По условию число васильков на 5 меньше, чем число ромашек, или число ромашек на 5 больше, чем число васильков. Воспользуемся определением отношения «больше на число 5», получаем, что множество ромашек (множество с большим числом элементов) можно разбить на два непересекающихся подмножества D и С, таких, что D равномощно множеству васильков, а число элементов второго С равно 5. Это означает, что ромашек столько, сколько васильков, да еще 5 (рис. 12).
Шаги построения:
1) А, m(А) = 12;
2) С, m(С) = 5, С ⊂ А;
3) существует D, D ⊂ А, D = СА;
4) В
D.
3. Нужно найти m(В), т. к. В
D, то m(В) = m(D) (1), D = СА, значит, m(D) = m(СА), m(D) = m(А) – m(С), т.е. m(D) = 12 – 5 (2)
Из (1) и (2) m(В) = 12 – 5.
Доказали, что число васильков нужно находить вычитанием.
4. В
N7 => m(В) = 7. Число васильков равно 7.
Рассмотрите еще один способ решения этой задачи. Сравните и выберите наиболее простой с вашей точки зрения.
Начнем со второго шага (построение модели). По условию число васильков на 5 меньше, чем число ромашек. Воспользуемся определением отношения «меньше на число», получаем, что васильков столько, сколько ромашек (множество D), но без 5 цветков (множество С). Из этого следует такое построение (рис. 13):
1) А, m(А) = 12;
2) D
А;
3) С, m(С) = 5,С ⊂ D;
4) существует В, В ⊂ D элементы которого васильки.
Найдем m(В). B
N7 => m(B) = 7.
Число васильков равно 7. Можно найти иначе. В = D\С, т.к. С ⊂ D, тогда В = СD, задачу будем решать вычитанием, а именно m(B) = m(D) – m(C) = 12 – 5, т.к. D
А, то m(D) = m(А).
Наиболее трудными будут задачи, в которых действие задано в косвенной форме.
Задача 5. В букете 12 ромашек, их на 5 больше, чем васильков. Сколько васильков в букете?
Сформулируйте условие иначе. По условию число ромашек на 5 больше, чем число васильков, поэтому васильков на 5 меньше, чем ромашек. Задачу с несколько измененным условием мы решаем, как предыдущую.
Отношения «равно» и «меньше»
Выясним, на какой теоретической основе происходит сравнение чисел.
Пусть даны два целых неотрицательных числа а и Ь. С теоретико-множественной точки зрения они представляют собой число элементов конечных множеств А и В: а = п(А), b = п(В). Если эти множества равномощны, то им соответствует одно и то же число, т. е. а=b. Приходим к определению:
Числа а и b равны, если они определяются равномощными множествами:
а = b А А
В, где n(А) = а, n(B) = b
Если множества A и В неравномощны, то числа, определяемые ими, различны.
В том случае, если множество А равномощно собственному подмножеству множества В и п (А) = а, п (В)= b, говорят; что число а меньше числа b, и пишут: а< b.В этой же ситуации говорят, что b больше а, и пишут: b>а,
а< b А В1, где B1 А В1, где B1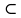 B и В1≠ В, В1≠0 B и В1≠ В, В1≠0
|
Из приведенных определений отношений «равно» и «меньше» исходят в начальной школе когда объясняют, что 2 = 2, 3 = 3, 2<3, 3<4 и т. д. Например, при введении записи 3 = 3 рассматривают два равномощных множества квадратов и кругов (рис. 91). При изучении отношения 3<4 проводятся рассуждения: возьмем три розовых кружка и 4 синих и каждый розовый наложим на синий, видим, что синий кружок остался незакрытым, значит, розовых кружков меньше, чем синих, поэтому можно записать: 3<4.
Отметим еще, что если числа а и b определяются соответственно множествами A и В (кружков, квадратов, палочек и т. д.) и aто выделение в множестве В собственного подмножества, равномощного множеству А, на практике происходит самыми различными способами: наложением, приложением, путем образования пар и т. д. Это возможно, так как отношение а (так же как и отношение а = b) не зависит от выбора множеств АиВ, таких, что n (А)=а, п (В) = b, важно только, чтобы А было равномощно собственному подмножеству множества В (а в случае равенства чисел А равномощно В).
Изложенный подход к определению отношения «меньше» имеет ограниченное применение, он может быть использован для сравнения чисел в пределах 20, поскольку связан с непосредственным сравнением двух групп предметов.
Как же можно еще сравнивать целые неотрицательные числа? Пусть а в смысле данного выше определения.
Тогда а = п(А), b = п(В) и АВ1, где В1— собственное подмножество множества В (рис. 92). Так как B1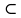 B, то В можно представить в виде объединения множества В1 и его дополнения В\В1. Обозначим это дополнение В1' (т. е. В\В1 = В1'. Тогда В= В1 B, то В можно представить в виде объединения множества В1 и его дополнения В\В1. Обозначим это дополнение В1' (т. е. В\В1 = В1'. Тогда В= В1 В1' и, следовательно, n (В1 В1' и, следовательно, n (В1 В1'). Поскольку множества В1 и В1' не пересекаются, то по определению АВ. суммы n(В)=n(B1) + n(В1') (*). Но по условию В1A, значит, п(В1) = п(A). Если число элементов в множестве В1 обозначить через с, то равенство (*) можно записать в виде b = а+с, т. е. из того, что а следует, что b = а+с. Нетрудно убедиться и в справедливости обратного утверждения. В1'). Поскольку множества В1 и В1' не пересекаются, то по определению АВ. суммы n(В)=n(B1) + n(В1') (*). Но по условию В1A, значит, п(В1) = п(A). Если число элементов в множестве В1 обозначить через с, то равенство (*) можно записать в виде b = а+с, т. е. из того, что а следует, что b = а+с. Нетрудно убедиться и в справедливости обратного утверждения.
Пришли к другому определению отношения «меньше»:
Число а меньше числа 6 тогда и только тогда, когда существует такое натуральное число с, что а + с =b.
Как, пользуясь этим определением, объяснить, что 3<7? 3<7, поскольку существует такое целое неотрицательное число 4, что 3+ 4 = 7.
Этот способ определения отношения «меньше» через сложение также используется в начальном курсе математики. Об этом говорит наличие пар записей 5+1=6, 6>5; 7+1=8, 7<8.
Рассмотрим еще один способ сравнения чисел.
Пусть а < b. Тогда про любое натуральное число х можно сказать, что если х≤а, то х Это значит, что при аотрезок натурального ряда Na является собственным подмножеством отрезка Nb. Справедливо и обратное утверждение.
Таким образом, получаем еще одно определение отношения «меньше»:
Число а меньше числа b тогда и только тогда, когда отрезок натурального ряда Na является собственным подмножеством отрезка этого ряда Nb:
a Na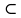 Nb и Na≠Nb . Nb и Na≠Nb .
Например, справедливость неравенства 3<7 с этих позиций можно объяснить тем, что (1, 2, 3)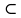 {1, 2, 3, 4, 5, 6, 7). {1, 2, 3, 4, 5, 6, 7).
Данная трактовка понятия «меньше» позволяет сравнивать числа, опираясь на знание их места в натуральном ряду.
Этот способ сравнения чисел также используется в начальном обучении математике: число, которое при счете встречается раньше, всегда меньше числа, которое идет позднее.
|
 Скачать 393.87 Kb.
Скачать 393.87 Kb.
 А В1, где B1
А В1, где B1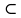 B и В1≠ В, В1≠0
B и В1≠ В, В1≠0
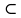 B, то В можно представить в виде объединения множества В1 и его дополнения В\В1. Обозначим это дополнение В1' (т. е. В\В1 = В1'. Тогда В= В1
B, то В можно представить в виде объединения множества В1 и его дополнения В\В1. Обозначим это дополнение В1' (т. е. В\В1 = В1'. Тогда В= В1 В1' и, следовательно, n (В1
В1' и, следовательно, n (В1 В1'). Поскольку множества В1 и В1' не пересекаются, то по определению АВ. суммы n(В)=n(B1) + n(В1') (*). Но по условию В1A, значит, п(В1) = п(A). Если число элементов в множестве В1 обозначить через с, то равенство (*) можно записать в виде b = а+с, т. е. из того, что а
В1'). Поскольку множества В1 и В1' не пересекаются, то по определению АВ. суммы n(В)=n(B1) + n(В1') (*). Но по условию В1A, значит, п(В1) = п(A). Если число элементов в множестве В1 обозначить через с, то равенство (*) можно записать в виде b = а+с, т. е. из того, что а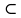 Nb и Na≠Nb .
Nb и Na≠Nb .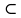 {1, 2, 3, 4, 5, 6, 7).
{1, 2, 3, 4, 5, 6, 7).



