Навигация по странице:Отношения «больше на», «меньше на».Пусть m(A) = a, m(B) = b и a, b NОпределение 7. Суммой любых целых неотрицательных чисел a и b называется число элементов объединения непересекающихся множеств А и В, таких, что a = m(А), b = m(В).В школе дети учатся решать задачи на сложение двух типовПоставим перед собой такие целиНа подготовительном этапе можно предложить такой алгоритм решенияЗ а д а н и е 3.П р и м е ч а н и е. Обосновать выбор действия можно иначе.Cумма а + b не зависит от выбора непересекающихся множеств A и В, таких, чтоДействие, при помощи которого находят сумму, называют сложением, а числа, которые складывают, называют слагаемыми.С переместительным свойством сложения учащиеся начальных классов знакомятся при изучении чисел первого десяткаПроанализируем эти способы.
|
Теор множ смысл + -. Правила вычитания числа из суммы и суммы из числа
Теоретико-множественный смысл сложения и вычитания на множестве целых неотрицательных чисел.
Отношения «равно», «меньше».
Отношения «больше на», «меньше на».
Правила вычитания числа из суммы и суммы из числа.
Мы можем изобразить объединение двух конечных множеств. Число элементов объединения двух конечных множеств можно найти, используя счет, т.е. установление взаимно однозначного соответствия между объединением множеств и отрезком натурального ряда.
Кроме того в теории множеств доказано, что число элементов объединения двух непересекающихся множеств равно сумме числа элементов первого и второго множеств.
К р а т к а я з а п и с ь : m(A U B) = m(A) + m(B) (1), если A ∩ B = Ø.
Пусть m(A) = a, m(B) = b и a, b No; сделав замену в равенстве (1), получим предложение a + b = m(A U B), из которого получается определение суммы чисел a и b.
Определение 7. Суммой любых целых неотрицательных чисел a и b называется число элементов объединения непересекающихся множеств А и В, таких, что a = m(А), b = m(В).
К р а т к а я з а п и с ь : a + b = m(А U В), где m(А) = a, m(В) = b, А ∩ В = Ø
Из определения суммы чисел a и b мы видим связь сложения двух целых неотрицательных чисел с объединением двух непересекающихся множеств. Связь объединения множеств со сложением чисел раскроем при решении текстовых задач.
З а д а н и е 2.
Найдите значение суммы 5 и 3.
Докажите, что 5 + 0 = 5.
Решение.
1. Воспользуемся определением суммы: 5 + 3 = m(АUВ) (1), где А∩В = Ø, 5 = m(А), 3 = m(В).
2. Изобразим АUВ (рис. 5), С = АUВ.
3. Найдем число элементов (АUВ) счетом, АUВNb => m(АUВ) = b(2) .
4. Используя (1) и (2), получим 5 + 3 = 8.
П р и м е ч а н и е. Обратите внимание на алгоритм решения: запись определения, построение модели, счет, вывод. Его можно использовать в дальнейшем и для нахождения значений разности, произведения, частного.
Пусть 5 = m(А), 0 = m(Ø).
По определению суммы, 5 + 0 = m(А U Ø), но А U Ø = А, значит, 5 + 0 = m(А), или 5 + 0 = 5.
В школе дети учатся решать задачи на сложение двух типов:
1) на конкретный смысл сложения;
2) на увеличение на число (в прямой и косвенной форме).
Поставим перед собой такие цели:
1) научиться раскрывать теоретико-множественный смысл решения задачи, чтобы обосновать выбор действия, которым нужно решать задачу;
2) научиться строить модели к задаче и отвечать на вопрос задачи, не выполняя действия над числами.
На подготовительном этапе можно предложить такой алгоритм решения:
работа с условием, выбор множеств;
• построение модели к решению. Модель считается построенной, если обосновано построение искомого множества;
• ответ на вопрос задачи;
• обоснование выбора действия.
• математическая модель построения задачи.
З а д а н и е 3. Обосновать выбор действия и ответить на вопрос.
Задача 1. На первой полке 6 книг, на второй – 4 книги. Сколько книг на двух полках вместе?
1. Работа с условием. Выбор множеств.
А – множество книг на первой полке, m(А) = 6,
В – множество книг на второй полке, m(В) = 4,
С – множество книг на двух полках, m(С) = ?
2. Модель к задаче (рис. 6).
Изобразим множество С, С – объединение множеств А и В, так как любая книга из множества С принадлежит множеству А или множеству В, С = А U В.
3. Нужно найти m(С), где С = А U В и А ∩ В = Ø, значит, задачу нужно решать сложением.
4. Используя счет, найдем m(С):
С
N10 => m(С) = m(N10), m(С) = 10.
Ответ: на двух полках 10 книг.
В ы в о д: 1. Доказали, что задачу нужно решать сложением.
2. Ответили на вопрос задачи.
П р и м е ч а н и е. Обосновать выбор действия можно иначе.
С = А U В и А∩В = Ø, тогда m(С) = m(А U В) или m(С) = m(А) + m(В), делаем замену и получаем m(С) = 6 + 4. Чтобы найти, сколько книг на двух полках, нужно сложить число книг на первой и второй полках.
Доказали, что задачу нужно решать сложением.
Задача 2. На первой полке 6 книг, на второй – на 3 книги больше. Сколько книг на второй полке?
1. Работа с условием. Выбор множеств.
А – множество книг на первой полке, m(А) = 6,
В – множество книг, m(В) = 3,
С – множество книг на второй полке, m(С) = ?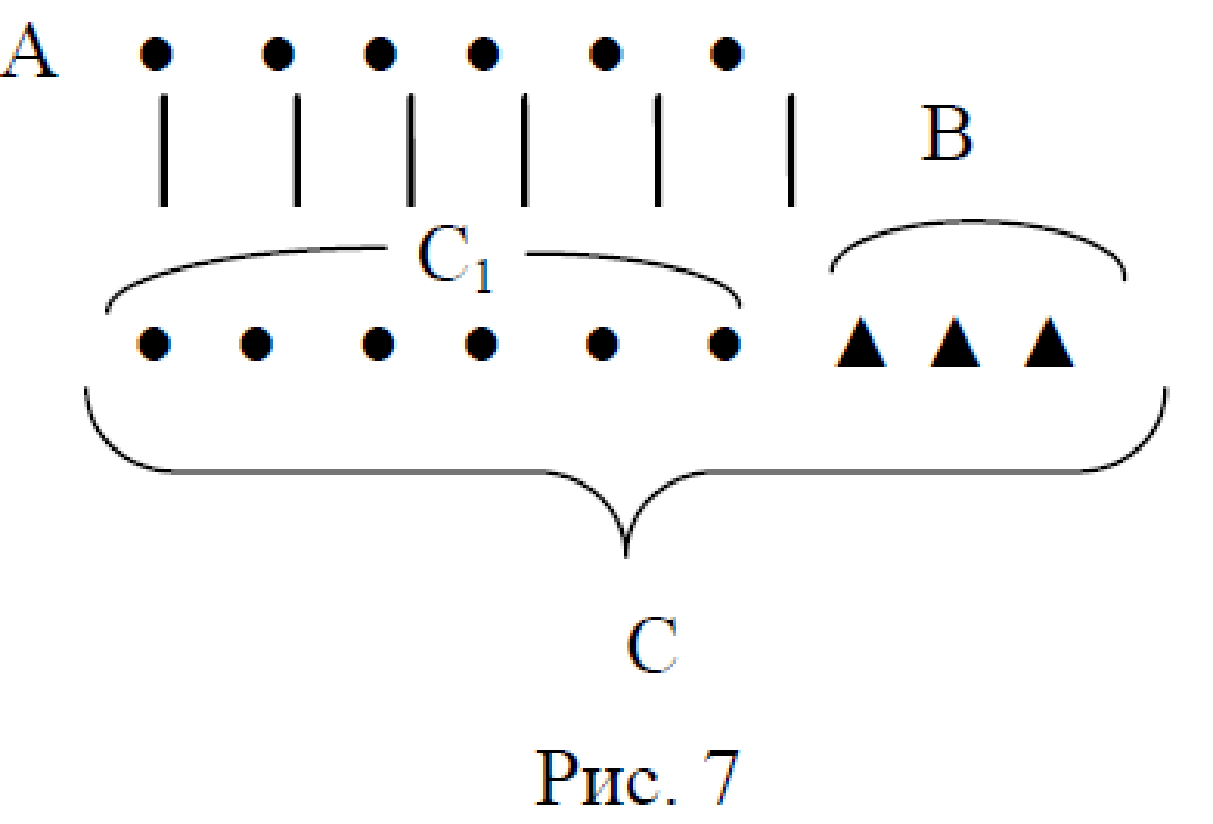
2. Изобразим множество С. По условию известно, что на второй полке на 3 книги больше, чем на первой. По определению отношения «больше на число» получаем, что на второй полке книг столько, сколько на первой (С1
А) да еще 3 книги (множество В).
Шаги построения модели (рис. 7):
1) А, m(А) = 6.
2) С1
A.
3) В, m(В) = 3.
4) С, С = С1UВ.
3. Нужно найти m(С), если С = С1 U В, С1 ∩ В = Ø, значит, задачу решаем сложением.
4. С
N9 => m(С) = m(N9), => m(С) = 9. На второй полке 9 книг.
П р и м е ч а н и е. С равно объединению двух непересекающихся множеств, значит, m(С) = m(С1) + m(В). Сделаем замену: m(С1) = m(А) = 6, так как С1
А m(С) = 6 + 3. Чтобы узнать число книг на второй полке, нужно сложить число книг на первой полке и число, которое показывает, на сколько больше книг на второй полке.
Задача 3. На первой полке 5 книг, это на 4 книги меньше, чем на второй полке. Сколько книг на второй полке?
При построении модели рассуждаем так: на первой полке книг на 4 меньше, чем на второй, значит, на второй полке на 4 книги больше, чем на первой, то есть на второй книг столько, сколько на первой да еще 4 книги. Модель такая же, как к задаче 1.
Говорят, что в этих задачах действие задано в косвенной форме: есть слова «на 4 книги меньше», а задачу решают сложением.
Задача 4. С первой полки взяли 6 книг, а со второй – на 4 книги больше. Сколько книг взяли с двух полок вместе?
Задача составная, нужно сформулировать две простые и решить каждую (см. образцы выше).
Cумма а + b не зависит от выбора непересекающихся множеств A и В, таких, что п (А) = а, п (В) = Ь. Это общее утверждение мы примем без доказательства.
Кроме того, сумма целых неотрицательных чисел всегда существует и единственна. Другими словами, какие бы два целых неотрицательных числа а и Ь мы ни взяли, всегда можно найти их сумму — целое неотрицательное число с, оно будет единственным для данных чисел а и Ь. Существование и единственность суммы вытекают из существования и единственности объединения двух множеств.
Действие, при помощи которого находят сумму, называют сложением, а числа, которые складывают, называют слагаемыми.
Выше нами было дано определение суммы двух слагаемых. А как определи а+ь сумму нескольких слагаемых?
Пусть сумма двух слагаемых определена и определена сумма п слагаемых. Тогда сумма, состоящая из n + 1 слагаемого, т. е. сумма a1 + <а2+ ...+ ап + аn +1» равна (ai+a2+ ... +аn)+аn + 1.
Например, чтобы найти сумму 2+7+15+19 согласно этому определению, надо выполнить следующие преобразования:
2+ 7+ 15+ 19 = (2 + 7+ 15)+19 = ((2 +7)+15)+19 =(9+ 15)+ 19 = 24+ 19=43.
Законы сложения
Докажем сначала переместительный закон, т. е. докажем, что для любых целых неотрицательных чисел а и b выполняется равенство а + b = =b + а.
Пусть а — число элементов в множестве А, b — число элементов в множестве В и А В=0. Тогда по определению суммы целых неотрицательных чисел а + b есть число элементов объединения множеств А и В: a+b=n (A В=0. Тогда по определению суммы целых неотрицательных чисел а + b есть число элементов объединения множеств А и В: a+b=n (A B). Но множество А B). Но множество А В равно множеству В В равно множеству В А согласно переместительному свойству объединения множеств, и, значит, п (А А согласно переместительному свойству объединения множеств, и, значит, п (А  В)= n (В В)= n (В ). По определению суммы п (В ). По определению суммы п (В А)=b+а, поэтому а+b=b+а для любых целых неотрицательных чисел а и b. А)=b+а, поэтому а+b=b+а для любых целых неотрицательных чисел а и b.
Докажем теперь сочетательный закон, т. е. докажем, что для любых целых неотрицательных
чисел а, b, с выполняется равенство(а+ b)+с=а+(b+с).
Пусть а = п (А), b=п(В), с=п(С), причем A В=0, B В=0, B C=0. Тогда по определению суммы двух чисел можно записать (a + b)+ с = n(A C=0. Тогда по определению суммы двух чисел можно записать (a + b)+ с = n(A )+n(C)= n((A )+n(C)= n((A ) )
Так как объединение множеств подчиняется сочетательному закону, то n((A UB) C) = n(AU(B C) = n(AU(B C)). Откуда по определению суммы двух чисел имеем п (A U(BUC)=n(A) + n (BUC) = a + (b + c). Следовательно, (a+b)+c =a+(b+c) для любых целых неотрицательных чисел а, b и с.Каково назначение сочетательного закона сложения? Он объясняет, как можно находить сумму трех слагаемых: для этого достаточно сложить первое слагаемое со вторым и к полученному числу прибавить третье слагаемое или прибавить первое слагаемое к сумме второго и третьего. Заметим, что сочетательный закон не предполагает перестановки слагаемых. C)). Откуда по определению суммы двух чисел имеем п (A U(BUC)=n(A) + n (BUC) = a + (b + c). Следовательно, (a+b)+c =a+(b+c) для любых целых неотрицательных чисел а, b и с.Каково назначение сочетательного закона сложения? Он объясняет, как можно находить сумму трех слагаемых: для этого достаточно сложить первое слагаемое со вторым и к полученному числу прибавить третье слагаемое или прибавить первое слагаемое к сумме второго и третьего. Заметим, что сочетательный закон не предполагает перестановки слагаемых.
И переместительный и сочетательный законы сложения могут быть обобщены на любое число слагаемых. При этом переместительный закон будет означать, что сумма не изменяется при любой перестановке слагаемых, а сочетательный — что сумма не изменяется при любой группировке слагаемых (без изменения их порядка).
Из переместительного и сочетательного законов сложения вытекает, что сумма нескольких слагаемых не изменится, если их переставить любым способом и если любую их группу заключить в скобки.
Вычислим, используя законы сложения, значение выражения 109 + 36+191 +64 +27.
На основании переместительного закона переставим слагаемые 36 и 191. Тогда 109 + 36+ 191 +64 + 27 = 109+ 191 +36 + 64 + 27.
Воспользуемся сочетательным законом, сгруппировав слагаемые, а затем найдем суммы в скобках: 109 + 191+ 36 + 64 + 27 = (109 + + 191) + (36 + 64)+27 = 300+ 100 + 27.
Применим еще раз сочетательный закон, заключив в скобки сумму чисел 300 и 100: 300+100+ 27 = (300+100)+ 27.
Произведем вычисления: (300+100) +27 = 400 + 27 = 427.
С переместительным свойством сложения учащиеся начальных классов знакомятся при изучении чисел первого десятка. Сначала оно используется при составлении таблицы сложения однозначных чисел, а затем для рационализации различных вычислений.
Сочетательный закон сложения в начальном курсе математики в явном виде не изучается, но постоянно используется. Так, он является основой приема прибавления числа по частям: 3 + 2 = 3 + (1 + 1)=(3+ 1)+1 =4+1=5. Кроме того, в тех случаях, когда надо прибавить число к сумме, сумму к числу, сумму к сумме, сочетательный закон используется в сочетании с переместительным. Например, прибавлять сумму 2+1 к числу 4 предлагается следующими способами:
4 + (2 + I)=4 + 3 = 7;
4 + (2+1) = 6+1=7;
4 + (2+1) = 5 + 2 = 7.
Проанализируем эти способы. В случае 1 вычисления выполнены в соответствии с указанным порядком действий. В случае 2 применено сочетательное свойство сложения. Вычисления же в последнем случае опираются на переместительный и сочетательный законы сложения, причем промежуточные преобразования опущены. Они таковы. Сначала на основании переместительного закона переставили местами слагаемые 1 и 2: 4 +(2+1) = 4+(1 +2). Затем воспользовались сочетательным законом: 4+(1 + 2) = (4+1) + 2.И,наконец, произвели вычисления согласно порядку действий (4+1)+ 2 = 5 + 2 = 7. |
|
|
 Скачать 393.87 Kb.
Скачать 393.87 Kb.



 В=0.
В=0. B). Но множество
B). Но множество 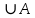 ). По определению суммы
). По определению суммы  )+n(C)= n((A
)+n(C)= n((A