Навигация по странице:Определение 3. Два целых неотрицательных числа a и b равны тогда и только тогда, когда равномощны множества, число элементов которых числа a и b .Отношение «равно» на множестве целых неотрицательных чисел – рефлексивно, симметрично и транзитивноК р а т к а я з а п и с ь : a А ВЕсли два множества неравномощны, то число элементов первого множества меньше числа элементов второго, или число элементов второго множества меньше числа элементов первого.Определение 5. Число а меньше b на число с, тогда и только тогда, когда в множестве В элементов столько, сколько в множестве А, да еще с элементов, если a = m(А), b = m(В).Отношение «меньше» антирефлексивное, антисимметричное и транзитивное . З а д а н и е 1.Правила вычитания числа из суммы и суммы из числа
|
Теор множ смысл + -. Правила вычитания числа из суммы и суммы из числа
Отношение «равно», «меньше», «меньше на число»
Возьмем множества А и В, пусть a = m(А), b = m(В), где a, b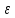 N0. N0.
Если А
В, то эти множества принадлежат одному классу эквивалентности, поэтому им соответствует одно и то же натуральное число, т.е. a = b .
Справедливо и обратное. Если a = b, то эти натуральные числа определяют один и тот же класс конечных равномощных множеств, значит, множества А и В равномощны. Из сказанного можно получить определение равных натуральных чисел.
Определение 3. Два целых неотрицательных числа a и b равны тогда и только тогда, когда равномощны множества, число элементов которых числа a и b .
К р а т к а я з а п и с ь : a = b  А А
В, где a = m(А), b = m(В).
Отношение «равно» на множестве целых неотрицательных чисел – рефлексивно, симметрично и транзитивно.
Если множества А и В не равномощные, тогда одно из множеств будет равномощно подмножеству другого множества, т.е. или А
В1 ⊂ В, или В
А1 ⊂ А .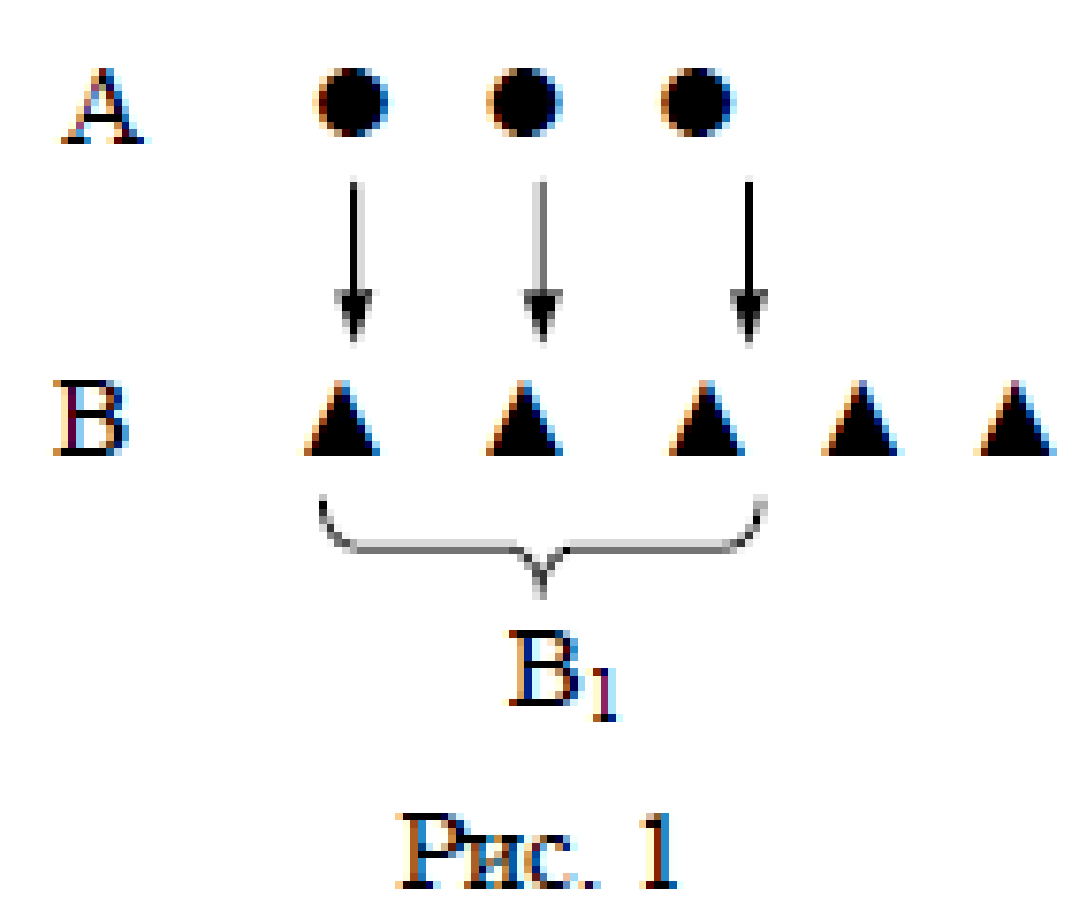
Пусть А
В1 ⊂ В (рис. 1). Видим, что в множестве В элементов столько, сколько в множестве А, да еще несколько, так как a = m(А), b = m(В), то говорят, что a < b . Справедливо и обратное.
Если a < b, то А
В1 ⊂ В, где a = m(А), b = m(В).
Определение 4. Натуральное число a меньше натурального числа b тогда и только тогда, когда множество, число элементов которого равно a, равномощно собственному подмножеству другого множества, число элементов которого равно b.
К р а т к а я з а п и с ь : a < b  А А
В1 ⊂ В, где a = m(А), b= m(В).
Если В
А1 ⊂ А, тогда получим, что b < a , где b = m(В), a = m(А).
Вывод. Если два множества неравномощны, то число элементов первого множества меньше числа элементов второго, или число элементов второго множества меньше числа элементов первого.
А
В1 ⊂ В можно прочитать еще так: в множестве В столько элементов, сколько в множестве А, да еще несколько (например, с) . Тогда можно сказать, что число а меньше b на число с .
Определение 5. Число а меньше b на число с, тогда и только тогда, когда в множестве В элементов столько, сколько в множестве А, да еще с элементов, если a = m(А), b = m(В).
Можно еще отметить, что в этом случае множество В разбито на два подмножества, в одном элементов столько, сколько в множестве А, а в другом с элементов.
Можно дать еще одно такое определение: «меньше на число с».
Определение 6. Число а меньше числа b на число с тогда и только тогда, когда множество В можно разбить на два непересекающихся подмножества, где число элементов одного равно числу а, а число элементов другого подмножества равно с.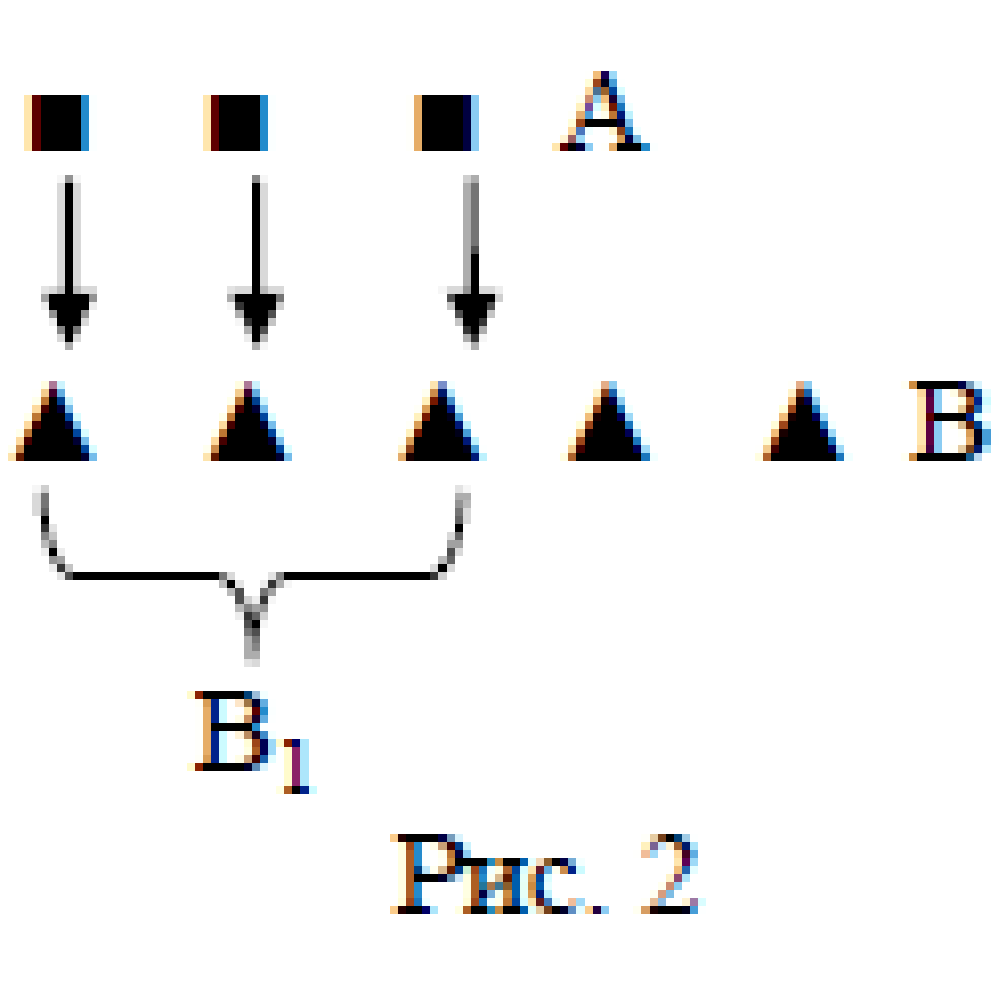
Очевидно, если число а меньше b на число с, тогда число b больше а на число с. Справедливо и обратное.
П р и м е ч а н и е. Отношение «меньше» антирефлексивное, антисимметричное и транзитивное.
З а д а н и е 1. Доказать: 1) 3 < 5 , 2) 0 < 5 , 3) 6 = 6, 4) 5 меньше 9 на 4 , 5) 6 больше 4 на 2.
1. Пусть 3 = m(А), А – множество квадратов. 5 = m(В), В – множество треугольников. Можно поставить в соответствие каждому квадрату треугольник (рис.2), тогда в множестве В выделяется подмножество В1, равномощное множеству А, получили А
В1 ⊂ В, тогда, по определению 4, 3 < 5.
2. Пусть 0 = m(Ø), 5 = m(А), где А – множество любых элементов. Из теории множеств известно, что все пустые множества равномощные и пустые множества являются подмножеством любого множества, т.е.
Ø
Ø ⊂ А => m(Ø) < m(А) или 0 < 5 .
3. Пусть 6 = m(А) и А – множество треугольников, 6 = m(В) и В – множество кругов (рис. 3). Можно поставить в соответствие каждому квадрату только один круг и каждому кругу можно поставить в соответствие только один треугольник. Получим А
В, т.е. m(А) = m(В) или 6 = 6 (по определению 3).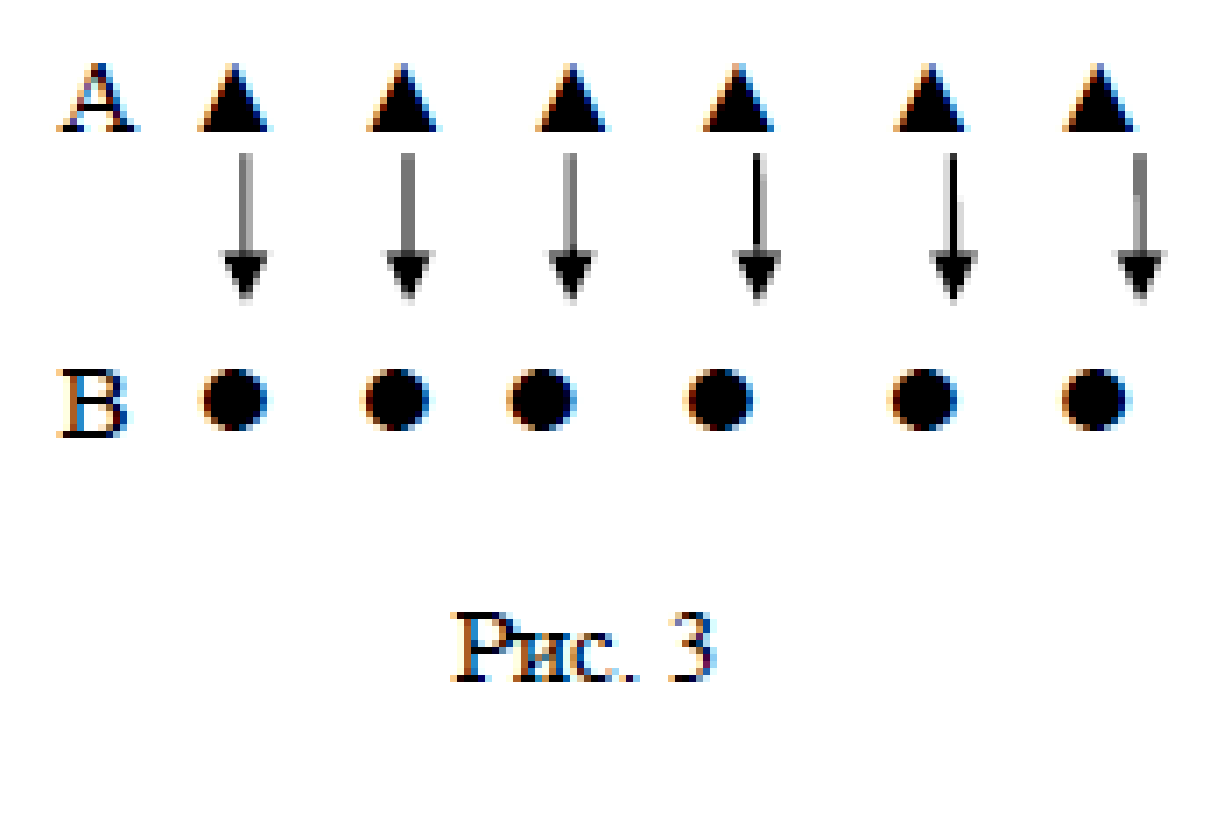
4. Пусть 5 = m(А) , где А – множество точек, 9 = m(В) , где В – множество кругов.
Изобразим А и В. Очевидно, что можно в множестве В выделить подмножество В1 равномощное множеству А, В1
А (рис. 4).
Множество В содержит столько элементов, сколько множество А, да еще несколько элементов, которые образуют множество С. Используем счет для нахождения числа элементов множества С. С
N4 , значит, m(С) = 4. По определению 5 получаем, что 5 меньше 9 на 4.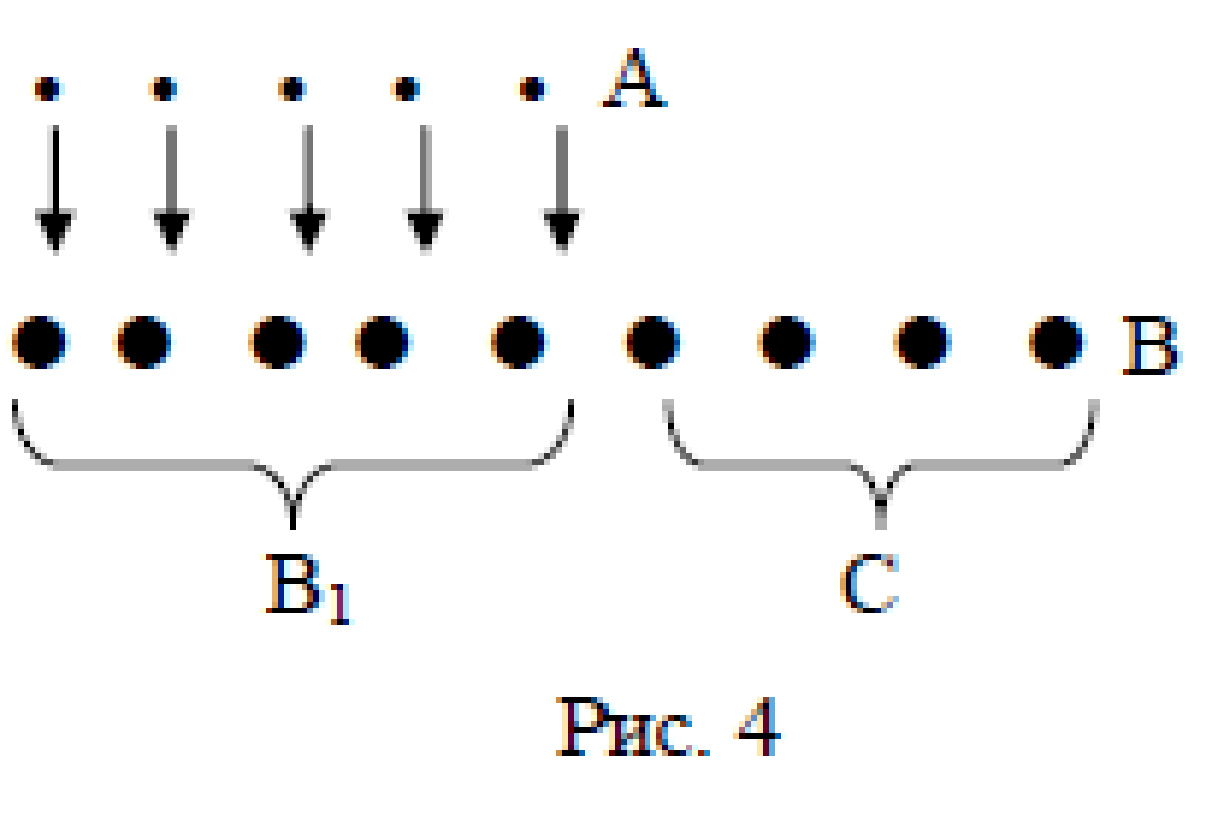
5. Пусть 6 = m(А), 4 = m(В). Нужно доказать, что 6 больше 4 на 2 или 4 меньше 6 на 2 (см. решение 4).
Правила вычитания числа из суммы и суммы из числа
Обоснуем известные правила вычитания числа из суммы и суммы из числа.
Правило вычитания числа из суммы. Чтобы вычесть число из суммы, достаточно вычесть это число из одного из слагаемых суммы и к полученному результату прибавить другое слагаемое.
Запишем это правило, используя символы:
Если а, b, с — целые неотрицательные числа, то:
а)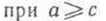 имеем, что (а + b) — с = (а - с) + b имеем, что (а + b) — с = (а - с) + b
б)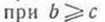 имеем, что (а +b) — с = а+(b — с) имеем, что (а +b) — с = а+(b — с)
в)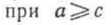 и и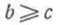 можно использовать любую из данных формул. можно использовать любую из данных формул.
Пусть а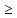 с, тогда разность а - с существует. Обозначим ее через р: а - с = р. Отсюда а = p+с. Подставим сумму р+с вместо а в выражение (а+ b) - с и преобразуем его:(а+b)- с=р+с + b) - с = р + b + с - с = р+b. с, тогда разность а - с существует. Обозначим ее через р: а - с = р. Отсюда а = p+с. Подставим сумму р+с вместо а в выражение (а+ b) - с и преобразуем его:(а+b)- с=р+с + b) - с = р + b + с - с = р+b.
Но буквой р обозначена разность а —с, значит, имеем (а + b)- с = (а - с)+b, что и требовалось доказать. Аналогично проводятся рассуждения и для других случаев.
Приведем теперь иллюстрацию данного правила (случай «а») при помощи кругов Эйлера. Возьмем три конечных множества А,В и С, такие, что п(А) = а, п(В) = b, п(С) = с и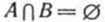  Тогда (а+b)-с есть число элементов множества Тогда (а+b)-с есть число элементов множества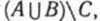 а число (а - с) +b есть число элементов множества а число (а - с) +b есть число элементов множества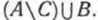 На кругах Эйлера множество На кругах Эйлера множество 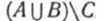 изображается заштрихованной областью, представленной на рисунке 97. изображается заштрихованной областью, представленной на рисунке 97.
Легко убедиться в том, что множество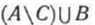 изобразится точно такой же областью. Значит, изобразится точно такой же областью. Значит,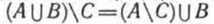 для данных множеств А, В и С. Следовательно, для данных множеств А, В и С. Следовательно, 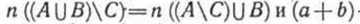 - с = (а - с) + b. - с = (а - с) + b.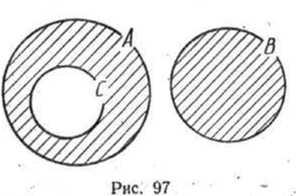
Правило вычитания из числа суммы. Чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т. е. если а, b, с - целые неотрицательные числа, то при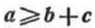 имеем а-(b+с)=(а -b) - с. имеем а-(b+с)=(а -b) - с.
Обоснование этого правила и его теоретико-множественная иллюстрация выполняются так же, как и для правила вычитания числа из суммы.
Приведенные правила рассматриваются в начальной школе на конкретных примерах, для обоснования привлекаются наглядные изображения. Эти правила позволяют рационально выполнять вычисления. Например, правило вычитания из числа суммы лежит в основе приема вычитания числа по частям: 5-2 = 5-(1 + 1)=(5-1)-1=4-1.= 3.
Смысл приведенных правил хорошо раскрывается при решении арифметических задач различными способами. Например, задача «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок. 5 лодок вернулись. Сколько лодок с рыбаками должно еще вернуться?» может быть решена тремя способами:
способ.
1. 20 + 8 = 28 2. 28-6 = 22
способ.
1. 20 — 6=14 2.14 + 8 = 22 III способ. 1.8 — 6 = 2 2.20 + 2 = 22
Упражнения
Докажите правило вычитания суммы из числа и проиллюстрируйте его при помощи кругов Эйлера.
Докажите правило: чтобы из разности двух чисел вычесть
третье число, достаточно из уменьшаемого вычесть сумму двух других чисел.
Найдите наиболее рациональным способом значение выражения:
1) (3748+ 10 392)-8392; 3) 763 + 945-263;
2) 7273 - (396 + 1173); 4) 568 - 229 - 168.
Нижеприведенные задачи решите различными способами, дайте обоснование:
В одной банке было 10 соленых огурцов, а в другой 6 огурцов. За обедом съели 4 огурца. Сколько всего огурцов осталось?
В гараже стояло 20 машин, сначала выехало 7 машин, а потом 3 машины. Сколько машин осталось в гараже?
Решите нижеприведенные две задачи и объясните, чем отличаются их решения:
В одной бочке 40 ведер воды. Утром на поливку цветов израсходовали 12 ведер, а вечером 10 ведер. Сколько ведер воды осталось в бочке?
|
|
|
 Скачать 393.87 Kb.
Скачать 393.87 Kb.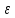 N0.
N0.
 А
А



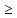 с, тогда разность а - с существует. Обозначим ее через р: а - с = р. Отсюда а = p+с. Подставим сумму р+с вместо а в выражение (а+ b) - с и преобразуем его:(а+b)- с=р+с + b) - с = р + b + с - с = р+b.
с, тогда разность а - с существует. Обозначим ее через р: а - с = р. Отсюда а = p+с. Подставим сумму р+с вместо а в выражение (а+ b) - с и преобразуем его:(а+b)- с=р+с + b) - с = р + b + с - с = р+b.