Четверная система фазового равновесия. курсовая четверная система фаз равнов. Правило фаз Гиббса

• Название: Правило фаз Гиббса
• Анкор: Четверная система фазового равновесия
• Дата: 29.11.2022
• Размер: 288.9 Kb.
• Имя файла: курсовая четверная система фаз равнов.docx
• Тип: Закон; #819885

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1.Диаграмма состояния 4

1.2 Правило фаз Гиббса (закон равновесия фаз) 6

1.3 Диаграмма состояния системы с простой эвтектикой 7

1.4 Понятия о геометрическом представлении диаграмм состояния четверных и других многокомпонентных систем 11

2.ГРАФИЧЕСКОГО АНАЛИЗ ФАЗОВОГО СОСТАВА ЧЕТВЕРНОЙ СИСТЕМЫ 15

2.1 Графический анализ фазового состава в твердом состоянии реальной четверной системы c четверным соединением 15

2.2 Диаграммы состояния четверных систем с нонвариантным эвтектическим равновесием 19

ЗАКЛЮЧЕНИЕ 24

Список литературы 25

ВВЕДЕНИЕ

Диаграмма состояния (фазовая диаграмма), графическое изображение всех возможных состояний термодинамической системы в пространстве основных параметров состояния температуры Т, давления P и состава X (обычно выражаемого молярными или массовыми долями компонентов).

Фазовый состав, структурные составляющие и характер крис­таллизации любого промышленного сплава являются важнейшими показателями, которые определяют его эксплуатационные и техно­логические свойства: прочность и пластичность, коррозионную стойкость, поведение при литье, обработке давлением, сварке и т. д. Научной основой анализа фазового состава (и частично микрострук­туры) являются диаграммы состояния.

Объект изучения данной курсовой работы – фазовые диаграммы четверной системы.

Предмет изучения – графический анализ фазового состояния четверной системы.

Целью данной работы является изучение тетраэдрической фазовой диаграммы простой четверной системы с эвтектикой.

Основные задачи:

– изучить закон равновесия Гиббса и основные типы диаграмм состояния;

– подробнее рассмотреть диаграммы состояния с простой эвтектикой;

– рассмотреть геометрическое представление диаграмм состояния четверных и других многокомпонентных систем;

– провести графический анализ фазового состава четверной системы.

Структура. Курсовая работа состоит из введения, двух глав, заключения и списка использованной литературы.

1. Диаграмма состояния

Для сложных систем, состоящих из многих фаз и компонентов, построение диаграммы состояния является единственным методом, позволяющим на практике установить, сколько фаз и какие конкретно фазы образуют систему при данных значениях параметров состояния. Каждое реально существующее состояние системы на диаграмме состояния изображается так называемой фигуративной точкой; областям существования одной фазы отвечают участки пространства (на трехмерных диаграммах состояния) или плоскости (на двухмерных диаграммах состояния), условиям сосуществования фаз - соответствует поверхности или линии; изменение фазового состояния системы рассматривается как движение фигуративной точки на диаграмме состояния. Анализ относительного расположения объемных участков, поверхностей, линий и точек, которые образуют диаграмму состояния, позволяет однозначно и наглядно определять условия фазового равновесия, появления в системе новых фаз и химических соединений, образования и распада жидких и твердых растворов и т.п.

Диаграммы состояния используют в материаловедении, металлургии, нефтепереработке, химической технологии (в частности, при разработке методов разделения веществ), производствах электронной техники и микроэлектроники и т.п.

С ее помощью определяют направленность процессов, связанных с фазовыми переходами, осуществляют выбор режимов термообработки, отыскивают оптимальные составы сплавов и т.п. Теоретическими основами построения и интерпретации диаграмм состояния равновесных систем являются:

– условие фазового равновесия, согласно которому химические потенциалы каждого компонента во всех фазах при равновесии равны;

– условие химического равновесия, согласно которому сумма химических потенциалов вступающих в реакцию веществ при равновесии равна аналогичной сумме для продуктов реакции;

– фаз правило Гиббса, согласно которому число компонентов К, число фаз Ф и вариантность системы v (т.е. число независимых параметров состояния, которые можно в определенных пределах изменять без изменения числа и природы фаз) связаны соотношением: v = К - Ф + 2. Цифра 2 означает, что учитываются только два интенсивных параметра состояния - температура и давление. Если учитываются и др. параметры, напр., напряженности электромагнитного или гравитационного полей, вариантность системы соотв. увеличивается. Различают нонвариантные (v = 0), моновариантные (v = 1), дивариантные (v = 2) и т.д. состояния (равновесия);

– правило о соприкасающихся пространствах состояния, согласно которому если два разных пространства состояния (поля в случае плоской диаграммы) соприкасаются по линии, то они различаются между собой на одну фазу, если поля соприкасаются в точке, то состояния различаются на две фазы. Для построения диаграмм состояния расчетным путем необходимо знать зависимости химических потенциалов всех компонентов системы от Т, P и состава фаз. Приближенные методы расчета с применением ЭВМ интенсивно развиваются, в частности, для многокомпонентных сплавов. Однако пока диаграммы состояния строят на основе экспериментальных данных, получаемых главным образом термическим анализом, который позволяет определять зависимости температур плавления или кристаллизации от состава, а также изучением равновесий жидкость - пар и жидкость - жидкость. Широко используют рентгеновский фазовый анализ, данные о микроструктуре затвердевших расплавов, измерения физических свойств фаз. Изучение диаграмм состояния составляет основное содержание физико-химического анализа.

1.2 Правило фаз Гиббса (закон равновесия фаз)

Общие закономерности, которым подчиняются равновес­ные гетерогенные системы, устанавливаются правилом фаз, вы­веденным Гиббсом в 1876 г. С помощью правила фаз может быть получен ответ на вопрос: «может ли данная сложная сис­тема существовать при различных произвольных значениях па­раметров или же требует параметров строго определенных или связанных между собою определенной зависимостью?». Боль­шое значение правила фаз состоит в том, что оно позволяет ре­шать поставленную задачу для любого числа веществ, обра­зующих данную систему.

Правило фаз Гиббса устанавливает соотношение между числом фаз Ф, числом компонентов К и числом степеней свобо­ды С.

Правило фаз может быть сформулировано следующим об­разом:

Число степеней свободы равновесной термодинамиче­ской системы, на которую из внешних параметров влияют только давление и температура, равно числу компонентов системы плюс два и минус число фаз:

C=K- Ф+2. (2)

Цифра 2 обозначает число независимых переменных (Т, Р), одинаковых для всех равновесных фаз. Если условие существо­вания системы кроме температуры и давления определяется еще каким-нибудь фактором интенсивности, то правило фаз Гиббса запишется в общем виде:

C = K - Ф + h , (3)

где h - число независимых переменных.

В том случае, если некоторые из параметров фиксированы, то число независимых переменных уменьшается. Например, ес­ли процесс идёт при постоянном давлении или постоянной тем­пературе, то закон равновесия фаз принимает вид:

C= K- Ф+ 1. (4)

Число степеней свободы может быть равно нулю или це­лому положительному числу (f = 0, 1, 2,...). По числу степеней свободы различают:

1. 
   нон- или инвариантные системы. Для них число степе­ней свободы равно 0 (С = 0);
   
2. 
   моно- или одновариантные. В этом случае число степе­ней свободы равно 1 (С = 1);
   
3. 
   би- или двухвариантные системы. Для них число степе­ней свободы равно двум (С = 2);
   
4. 
   n-вариантные (С = n) системы.
   

Общим условием равновесия фаз в многокомпонентной сис­теме является равенство факторов интенсивности, характери­зующих состояние каждой из фаз. Факторами интенсивности многокомпонентной системы в простейшем случае являются температура, давление и химические потенциалы каждого из компонентов.

1.3 Диаграмма состояния системы с простой эвтектикой

Диаграмма состояния двухкомпонентной системы эвтекти­ческого типа в координатах температура - состав представлена на рис. 11.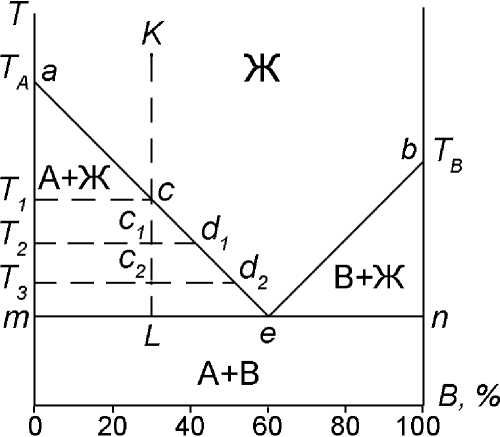



Рис. 1.2.1. Диаграмма состояния системы с простой эвтектикой
Диаграмму состояния системы с простой эвтектикой ус­ловно можно разбить на четыре области. Выше линии aeb суще­ствует одна жидкая фаза - расплав, состоящий из компонентов А и B. По линии ae кристаллизуется компонент А, по линии be - компонент B. Линии ae и eb называются линиями ликвидуса. В области aem в равновесии жидкая фаза и кристаллы А, в области ben - жидкая фаза и кристаллы B. Ниже линии men присутству­ют только твердые фазы А и B.

Точка, отображающая состояние системы, называется фи­гуративной точкой. Возьмем фигуративную точку K. Как видно из рис. 5, в этой точке в системе присутствует только жидкая фаза, состав которой можно определить, опустив перпендикулярна ось абсцисс. Жидкая фаза в точке К состоит из 30 % В и 70 % А. При понижении температуры фигуративная точка перемеща­ется по линии KL. При понижении температуры до T₁ фигура­тивная точка попадает на линию ae (точка с). В этой точке на­чинают выпадать кристаллы А. При дальнейшем понижении температуры количество кристаллов А увеличивается, при этом состав жидкой фазы меняется по линии ae. Допустим, что тем­пература понизилась до T2, фигуративная точка придет в точку с₁. В этой точке в равновесии находится жидкая фаза состава d₁, содержащая 60 % А и 40 % В, и кристаллы компонента А.

Для определения составов сосуществующих фаз через фи­гуративную точку проводят прямую, параллельную оси абсцисс (например, T2d1). Прямая, соединяющая точки, представляющие сосуществующие фазы, называется нодой. Спроецировав точки Т₂ и d₁ на ось составов, получим составы сосуществующих фаз.

С помощью диаграмм состояния можно определять не только состав, но и относительные количества сопряженных фаз. Согласно правилу рычага, количества сопряженных фаз об­ратно пропорциональны отрезкам, на которые делит ноду фигу­ративная точка. При этом количества фаз могут быть выражены в числах молей (если на оси абсцисс состав отложен в мольных долях или в мольных процентах) или в массах фаз (если он от­ложен в массовых долях или в массовых процентах). Проведем линию, соединяющую точки, соответствующие составу фаз, на­ходящихся в равновесии (ноду). Примем отрезок T2d1 за 100 %, тогда отрезок Т2с1 соответствует количеству жидкой фазы, а c1d1 - твердой, т. е. в равновесии находятся 25 % А и 75 % жид­кой фазы состава 60 % А и 40 % В. При дальнейшем перемеще­нии фигуративной точки она придет в точку с₂. Опять в равно­весии находятся жидкая и твердая фазы. Состав твердой фазы по прежнему 100 % А, состав жидкой фазы изменится, будет со­ответствовать составу точки d₂. Изменится и количественное соотношение фаз. Теперь за 100 % нужно принять отрезок T3d2: отрезок Т3с2 соответствует количеству жидкой, а отрезок c2d₂- твердой фаз. Как можно рассчитать, это будет 40 % А и 60 % жидкой фазы состава точки d2 (50 % А, 50 % В). При дальней­шем охлаждении фигуративная точка придет в точку L, состав жидкой фазы будет соответствовать составу эвтектики (точка e). 32

Отрезок me принимаем за 100 %. Как видно на рис. 11, отрезок mL равен отрезку Le, следовательно в равновесии находится 50 % кристаллов А и 50 % жидкости эвтектического состава (40 % А, 60 % В).

В точке L из жидкой фазы начнут выделяться кристаллы эвтектического состава. Расплавы, которые могут находиться в равновесии с кристаллами обоих компонентов, называют жид­кой эвтектической смесью или жидкой эвтектикой. Жидкая эвтектика в процессе кристаллизации переходит в твердую эв­тектику. Вследствие постоянства состава жидкой фазы кристал­лизация эвтектической смеси протекает при постоянной темпера­туре, подобно кристаллизации индивидуального вещества.

Твердая фаза обогащается компонентом В (до этого ком­понент В не выделялся). Состав твердой фазы будет меняться по линии mL, и когда он придет в точку L, состав которой совпадет с составом точки K, то исчезнут последние капли жидкости. Да­лее происходит охлаждение твердых фаз.

Для качественного правильного представления о диаграмме других сведений не требуется, хотя для точного нанесения всех кривых потребовалось бы длительное и часто очень сложное лабораторное исследование. Второй характеристикой, представляющей особый интерес, является то, что форма диаграммы ТХ для каждого данного давления может быть получена непосредственно из диаграммы РТ.

Составы фаз, конечно, не могут быть получены из РТ-диаграммы, но расположение нескольких фаз по их составу дается такой схематической диаграммой ТХ правильно. Таким образом, можно получить диаграмму ТХ, которая способна дать ответ на многие практические вопросы и которую можно превратить в полуколичественную при помощи весьма немногих добавочных данных, например измерением точных температур одновариантных реакций и определением составов трех сопряженных фаз, участвующих в этих реакциях.

1.4 Понятия о геометрическом представлении диаграмм состояния четверных и других многокомпонентных систем

В основу построения двойных систем положена ось концентраций, концы которой представляют собой чистые компоненты А и В. Тройные сис­темы строят на основе равностороннего (концентрационного) треугольника, любая точка которого, расположенная внутри его изображает состав тройно­го сплава, а вершины углов - чистые компоненты А, В и С. Для изображения состава четверных систем одной плоскости недостаточно, приходится ис­пользовать пространственный метод. Этот метод впервые предложил знаме­нитый русский кристаллограф Е.С. Федоров. Метод заключается в том, что состав сплава изображается при помощи правильного тетраэдра («концен­трационного тетраэдра»), представляющего собой тело, ограниченное че­тырьмя равносторонними треугольниками (рисунок 1.4.1). Вершины углов тетраэдра соответствуют чистым компонентам А, В, С и D. Ребра тетраэдра представляют собой оси концентраций двойных систем: А-В, А-С, А-D, В-С,

В-D и С-D. Грани тетраэдра изображают концентрационные треугольники тройных систем: А-В-С, А-В-D, А-С-D и В-С-D. Таким образом, фигуратив­ные точки двойных сплавов будут находиться на ребрах тетраэдра, тройных - на гранях и четверных - внутри тетраэдра.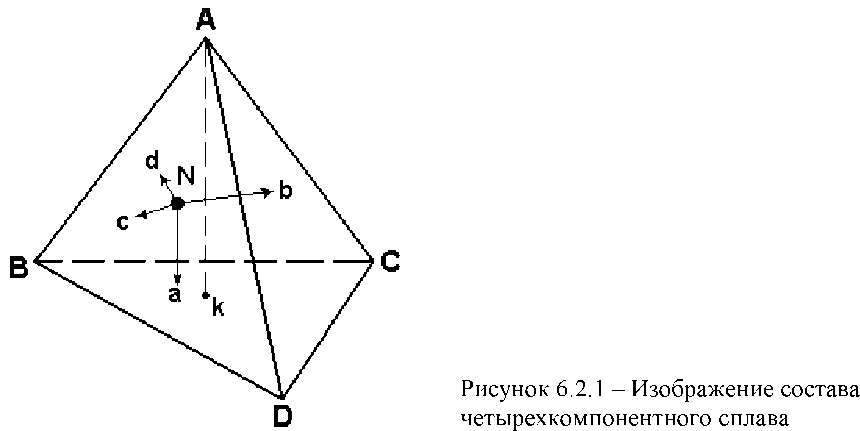

Рис. 1.4.1. Изображение четырехкомпонентного сплава
Правильный тетраэдр обладает следующими свойствами:

• 
  сумма длин перпендикуляров, опущенных из любой точки, находящейся внутри тетраэдра, на его грани, равна высоте тетраэдра;
  
• 
  сумма линий, проведенных из любой точки, находящейся внутри тетраэдра, параллельно его ребрам, равна длине ребра тетраэдра.
  

Используя эти свойства, при определении состава любого четверного сплава можно принять за единицу или 100 % высоту или длину ребра тетра­эдра.

Рассмотрим сплав N, фигуративная точка которого находится внутри тетраэдра (рисунок 1.4.1). Ак - это высота тетраэдра. Из точки N на грани тетраэдра опущены перпендикуляры: Na, Nb, Nc и dN (Na+Nb+Nc+dN=Ak). В этом случае фигуративная точка сплава N будет соответствовать содержа­нию компонентов:

Na Nb

X = — .100%; х_{в =} -2^.100%;

^A Ak B Ak

Nc Nd

X_c = —. 100%; X_n = —. 100%.

^C Ak ^D Ak

Фигуративную точку, отвечающую искомому составу, можно опреде­лить в пересечении плоскостей, выражающих определенное количество каж­дого из компонентов.

Правило фаз Гиббса для четверной системы при постоянном давлении можно записать в виде выражения: с=4-Ф+1=5-Ф.

Переменными, определяющими состояние четырехкомпонентной сис­темы, являются температура и три концентрации компонентов в фазах (чет­вертая концентрация определяется по разности из ста или единицы).

Необходимо заметить, что все три пространственные координаты в тетраэдре исчерпаны для определения концентраций компонентов. Поэтому температурная ордината может быть построена только в четырехмерном про­странстве. Следовательно, диаграмму состояния четырехкомпонентной сис­темы представляет четырехмерная фигура, что очень сложно представить в пространстве.

Каждой температуре должна соответствовать своя модель четверной системы.

Сечения, избираемые для исследования и анализа диаграммы состоя­ния четырехкомпонентной системы, могут быть различными в зависимости от условий, цели или приема исследования.

Наиболее целесообразен выбор сечений, параллельных либо граням тетраэдра, либо его перекрещивающимся ребрам.

На сечениях, параллельных граням тетраэдра, концентрация одного из компонентов системы, например ХА, постоянна для всех четверных сплавов сечения, концентрация остальных трех компонентов определяется из посто­янства их суммы Х_В+Х_C+Х_D=const (см. рисунок 1.4.2,а).

Сечения, параллельные перекрещивающимся ребрам тетраэдра, пере­секают все четыре грани тетраэдра, образую прямоугольник, в частном слу­чае - квадрат, когда сечение пересекает середины ребер (см. рисунок 1.4.2,б).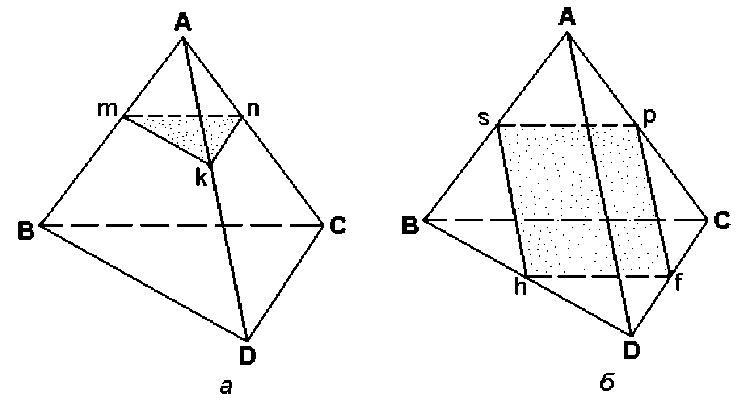



Рисунок 1.4.2 - Сечения тетраэдра: а - параллельное грани BCD, б - параллельное ребрам ВС и AD

Проблемы создания новых многофункциональных материалов со спе­циальными свойствами сталкиваются с трудностями определения критиче­ских точек, и в первую очередь, температур ликвидуса и солидуса, поскольку такие сплавы оказываются многокомпонентными, а многих соответствую­щих фазовых диаграмм состояния до сих пор не построено.

Даже наличие построенных трехкомпонентных и более сложных диа­грамм фазового равновесия не всегда решает проблему определения с доста­точной для практического использования точностью температур начала и конца плавления и кристаллизации сплавов. Многокомпонентные системы представляют в виде ограниченного числа разрезов и сечений, чаще всего изотермических, которые не включают подробную информацию о темпера­турах критических точек конкретных сплавов во всем многообразии их со­ставов.

2. ГРАФИЧЕСКОГО АНАЛИЗ ФАЗОВОГО СОСТАВА ЧЕТВЕРНОЙ СИСТЕМЫ

2.1 Графический анализ фазового состава в твердом состоянии реальной четверной системы c четверным соединением

Данный метод изображения рассматривается на примере алю­миниевого угла диаграммы Al—Si—Mg—Fe (рис. 2.1). Для алюми­ниевых сплавов главной фазой является алюминиевый твердый рас­твор — (Al), поэтому вершины концентрационного треугольника (т. е. проекции четверной диаграммы Al—Si—Mg—Fe) представляют собой фазы из двойных систем, находящиеся в равновесии с (Al):

(Si), A^Mg5 и A^Fe из систем Al—Si (см. рис. 5.12, д), Al—Mg и Al—Fe.

На двух сторонах располагают­ся фазы из тройных систем: Mg2Si из системы Al—Si—Mg (см. рис. 6.6), A^Fe₂Si и Al5FeSi из системы Al—Si—Fe .

Из такого рас­положения вытекает наличие двух трехфазных областей на стороне (Si)-Al8Mg5 ((Al) +Al8Mg5 + Mg₂Si и (Al) + (Si)+Mg₂Si) и трех трех­фазных областей на стороне (Si)—A^Fe ((Al) + (Si)+Al5FeSi, (Al)+Al5FeSi+Al8Fe2Si и (Al)+Al8Fe2Si +Al3Fe).

В алюминиевом углу диаграммы Al—Fe—Mg нет тройных фаз, поэтому вся третья сторона представляет собой одну трехфазную область: (Al)+Al8Mg₅+A^Fe. Внутри концентрационного треугольника име­ется четверное соединение Al8FeMg₃Si₆, которое находится в равно­весии с фазами (Si), Al5FeSi и Mg2Si, образуя соответствующие квазитройные сечения (в твердом состоянии).

Как следует из рис. 2.1, в алюминиевом углу диаграммы Al—Si—Mg—Fe в твердом состоянии имеются следующие четырех­фазные области с участием (Al): (Al) + (Si) + Mg2Si + Al8FeMg₃Si₆, (Al) + (Si) + Al5FeSi +Al8FeMg3Si6, (Al) + Mg₂Si + Al5FeSi +Al8FeMg3Si6, (Al) + Mg₂Si + Al5FeSi + Al8Fe2Si, (Al) + Mg2Si + Al8Fe2Si + Al3Fe, (Al) + Mg2Si +Al3Fe+Al8Mg5. Составы всех избыточных фаз кроме (Al) практически постоянны, а состав (Al) из-за низкой растворимости железа в твердом алюминии можно оценить по тройным диаграммам Al—Si—Mg (см. рис. 6.6) и Al—Si—Fe.

Для определения фазового состава заданного сплава системы Al—Si—Mg—Fe надо определить его положение на рис. 2.1. Для этого необходимо нормировать концентрации кремния, магния и железа ис­ходя из того, что сумма их относительных концентраций равна 100 %.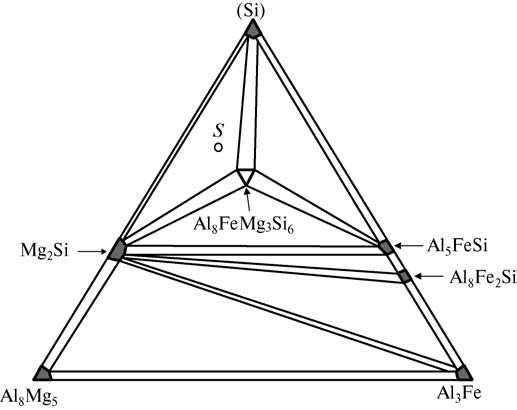



Рис. 2.1. Распределение фазовых областей в твердом состоянии в алюминиевом уг­лу системы Al—Si—Mg—Fe
Например, сплаву A1—7 % Si—2 % Mg—1 % Fe будет соответствовать точка £ (70 отн.% Si—20 отн.% Mg—10 отн.% Fe), что отвечает попада­нию в фазовую область (Al) + (Si) + A^FeSi + A^FeMg3Si6.

Далее рассматривается построение двух изотермических разре­зов данной системы в области алюминиевого угла. Первый из них при 7% Si и 200 ^оС (до 1 % Fe и до 2 % Mg) приведен на рис. 2.2, а. При такой температуре растворимости магния и кремния состав­ляют сотые доли процента, поэтому все фазовые области данного разреза можно достаточно точно определить по методике, рас­смотренной в гл. 11. На разрезе при 7% Si и 200 ^оС имеются толь­ко две четырехфазные области (Al) + (Si) + Mg2Si + A^FeMg3Si6 и (Al) + (Si) + A^FeSi + A^FeMg3Si6, которые разделены узкой полосой трехфазной области (Al) + (Si) + A^FeMg3Si6. Именно наклон по­следней и определяет строение этого простого разреза.

Второй разрез при 0,2 % Fe и 200 ^оС (до 2% Si и до 2 % Mg) имеет гораздо более сложное строение и содержит пять четырех­фазных областей (рис. 2.2, б). Чтобы не загромождать рисунок, на этом разрезе не отмечен алюминиевый твердый раствор (Al), присутствующий во всех фазовых областях, а также не обозначены четырехфазные области (так как все фазы легко определяются).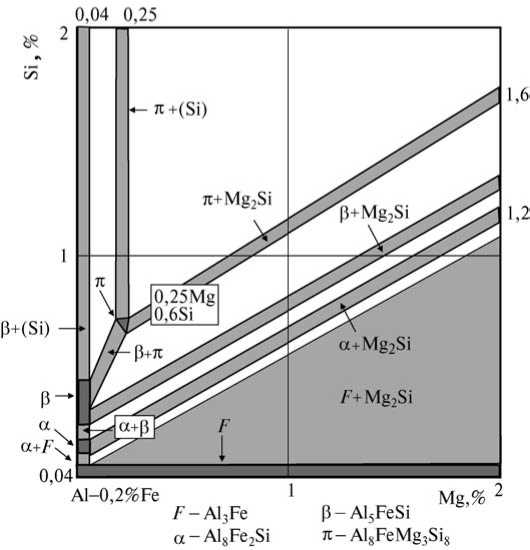




Рис. 2.2. Изотермические разрезы диаграммы Al—Fe—Mg—Si при 200 ^оС: а — 7%Si; б — 1%Fe

Из-за высокой растворимости магния в (Al) (даже при такой низкой тем­пературе она выше 2 % в трехфазных областях (Al) + Mg2Si + Al8Mg5 и (Al) + Al3Fe + Al8Mg5)) возникают трудности при определении фа­зовых границ в нижней части разреза. Если растворимости всех трех компонентов низки, то изотермический разрез при 0,2 % Fe содер­жал бы практически все фазовые области, показанные на рис. 2.1.1. В данном случае отсутствуют обе четырехфазные области с фазой Al8Mg5, а именно они должны располагаться вблизи исходного сплава Al—0,2 % Fe. Положение многих точек требует расчета.

Сначала рассмотрим двойной (исходный) и тройные сплавы, которые определяют фазовые области разреза вдоль соответствую­щих сторон. Сплав Al—0,2 % Fe во всем интервале температур ниже 655 ^оС и согласно диаграмме Al—Fe имеет фазовый состав (Al) + Al3Fe. Этот фазовый состав не меняется и при добавле­нии магния (при 440 ^оС), что видно из диаграммы Al—Mg—Fe. Влияние кремния более сложное, при добавлении этого эле­мента к исходному сплаву последовательно чередуются три трехфаз­ные области (Al)+ Al3Fe +Al8Fe2Si, (Al) + Al8Fe2Si + Al5FeSi и (Al) + Al5FeSi + (Si), что следует из диаграммы Al—Si—Fe (см. рис. 8.5). Оче­видно, что эти трехфазные области на изотермическом разрезе долж­ны по прямым линиям граничить с четырехфазными, при этом по­следние содержат те же фазы плюс одну новую (рис.2.1.2, б).

Строение данного разреза в значительной мере определяется положением двухфазной области (Al) + Al8FeMg₃Si6, которая в ре­альном масштабе очень мала, а на рис.2.2, б показана в виде треу­гольника (в общем случае такие линии явлются кривыми). Отметим, что вокруг каждой из трех вершин этой двухфазной области имеется одинаковое чередование числа фаз в смежных областях: 2—3—4—3. Вершины этого треугольника соприкасаются с тремя четырехфазны­ми областями, а стороны — с тремя трехфазными областями, имею­щими вид узких полосок.

2.2 Диаграммы состояния четверных систем с нонвариантным эвтектическим равновесием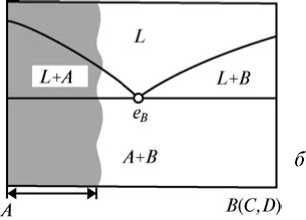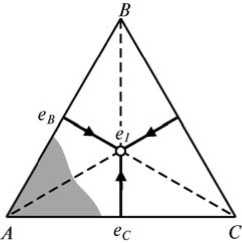

Рис. 2.2.1. Политермическая проекция диа­граммы A—B—C—D (а) в области вершины А c нонвариантным эвтектическим равно­весием при отсутствии растворимости в твердом состоянии:

б — диаграмма А—В; в — диаграмма А—В—С
Для качественного анализа характера кристаллизации четвер­ных сплавов используют политермическую диаграмму, которая представляет собой проекцию политермических (моновариантных) линий на концентрационный треугольник. Для системы эвтектиче­ского типа (при отсутствии растворимости в твердом состоянии и промежуточных соединений) такая политермическая диаграмма показана на рис. 2.2.1, а. Отметим, что все двойные диаграммы име­ют вид, показанный на рис. 2.2.1, б, а тройные — на рис. 2.2.1, в.


а



В этой четверной системе имеются одна пятифазная нонвариантная реакция Le^ A + B + C + D, которой соответствует точка E, и три мо- новариантные четырехфазные реакции (L^ A + B + C, L^ A + B + Dи L^ A + C + D). Последним отвечают линии е—Е, e2-E и ез-Е, которые разделяют весь концентрационный треугольник на три об­ласти (B-ei-E—ез, C-е ₁—Е—е₂, D—e2-E—e3). Попадание точки сплава в ту или иную область определяет, какая двойная эвтектика будет образовываться (L^ A + B, L^ A + C или L^ A + D). При таком изображении рассматриваются только сплавы, в которых за­ведомо первично кристаллизуется основная фаза (т. е. А на рис. 2.2.1). Проекция ликвидус на политермической диаграмме отсутствует, а проекции остальных поверхностей приведены в табл. 2.2.1. Воз­можные реакции, протекающие при кристаллизации различных четверных сплавов системы A—B—C—D эвтектического типа, даны в табл. 2.2.2. Поскольку рассматривается случай отсутствия раство­римости в твердом состоянии, то после завершения кристаллиза­ции по нонвариантой эвтектической реакции (Le^ A + B + C + D) никаких превращений не происходит (только охлаждение фаз-ком­понентов A, B, C и D).
Таблица 2.2.1. Проекции поверхностей четверной диаграммы с нонвариантным эвтектическим равновесием при отсутствии растворимости в твердом состоянии

Область*	Название поверхности	Фазовая граница
B–e1–E–e2	Начало кристаллизации двойной эвтектики	L+A/L+A+B
C–e1–E–e3	Начало кристаллизации двойной эвтектики	L+A/L+A+C
D–e2–E–e3	Начало кристаллизации двойной эвтектики	L+A/L+A+D
B–C–D	Эвтектическая плоскость-солидус	A+B+C+D/L+A+B+C,
		L+A+B+D, L+A+C+D
B–e1–E	Начало кристаллизации тройной эвтектики	L+A+B/L+A+B+C
C–e1–E	Начало кристаллизации тройной эвтектики	L+A+C/L+A+B+C
C–e2–E	Начало кристаллизации тройной эвтектики	L+A+C/L+A+C+D
D–e2–E	Начало кристаллизации тройной эвтектики	L+A+D/L+A+C+D
B–e3–E	Начало кристаллизации тройной эвтектики	L+A+B/L+A+B+D
D–e3–E	Начало кристаллизации тройной эвтектики	L+A+D/L+A+B+D

Таблица 2.2.2. Возможные фазовые превращения в сплавах четверной системы с нонвариантным эвтектическим равновесием при отсутствии растворимости в твердом состоянии

В качестве примера рассмотрим кристаллизацию сплава Х (рис.2.2.2, а). Состав этого сплава попадает в область C-e₁-E-e₂, поэтому в нем образуется двойная эвтектика L^ A + C, при этом со­став жидкости (относительный) изменяется вдоль прямой от точки X до точки Y. Далее кристаллизуется тройная эвтектика L^ A + C + D, состав жидкости в процессе этой моновариантной реакции меняется вдоль политермы e^-E. Заканчивается кристаллизация сплава X (как и всех других четверных сплавов этой системы) нонвариантной эвтектической реакцией. Кривая охлаждения этого сплава приведе­на на рис. 13.2, б, а соответствующие изменения в микроструктуре на разных этапах кристаллизации схематически показаны на рис. 2.2.3. При этом следует ожидать, что с увеличением числа фаз дисперс­ность эвтектики будет возрастать (т. е. четверная эвтектика — самая дисперсная).

Если состав сплава попадает на моновариантную эвтектичес­кую политерму (e-E, e^-Eили ез-E), то после образования первич­ных кристаллов компонента A сразу начнется образование соответ­ствующей тройной эвтектики. Попадание сплава на изотерму эвтектической плоскости (B-Е, C-Е или D-E) означает отсутствие стадии образования тройной эвтектики (т. е. после двойной эвтекти­ки происходит нонвариантная эвтектическая реакция). При нали­чии заметной растворимости в твердом состоянии подобный анализ

становится менее строгим. Однако новых путей кристаллизации (по сравнению с указанными в табл. 2.2.2) для сплавов, в которых кристаллизация заканчивается нонвариантной эвтектической реак­цией, не появится.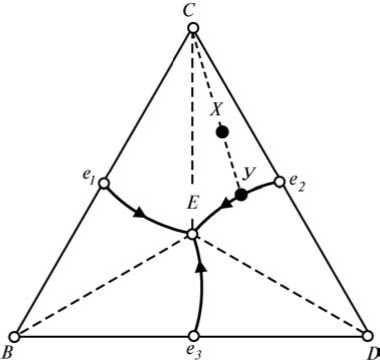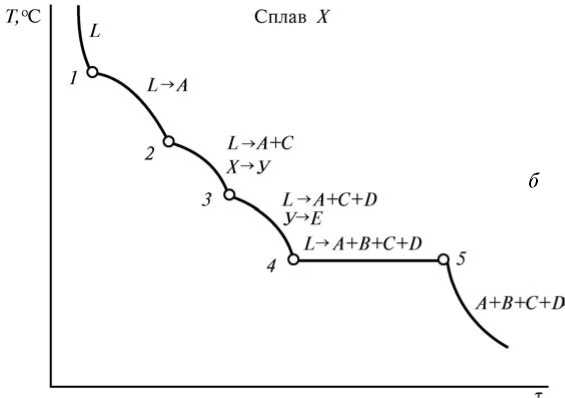


Рис. 2.2.2. Кривая охлаждения сплава Х системы A—B—C—D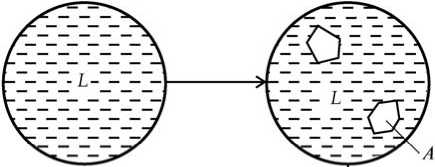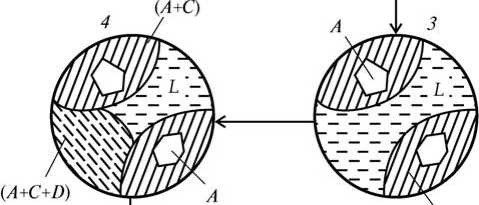




(Л+О
Рис. 2.2.3 Схема изменения микрост­руктуры сплава Х (см. рис. 2.2.2) в про­цессе кристаллизации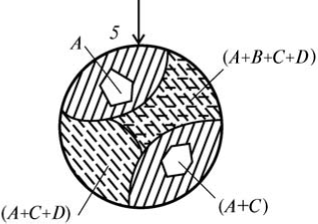



В процессе кристаллизации тройных эвтектик составы фаз при данной температуре находятся в вершинах соответствующего изо­термического тетраэдра. Поскольку твердые фазы имеют постоян­ный состав, то при понижении температуры изменяется положение только одной вершины, отвечающей составу жидкой фазы. Напри­мер, реакции L^ A + C + D отвечает конодный тетраэдр A—L—C—D, при этом состав жидкости L меняется вдоль политермы e^-E. В част­ности, применительно к сплаву X (рис. 2.2.3) в первый момент этой ре­акции (точка 3 на рис. 2.2.2, б) состав жидкости соответствует точке Y(см. рис. 13.2, а). В пространственной диаграмме точка X должна на­ходиться на грани A-Ly-C конодного тетраэдра A-Ly-C-D. При сни­жении температуры точка X оказывается внутри тетраэдра, который перед началом нонвариантой эвтектической реакции Le^ A + B + C + D(точка 4 на рис. 2.2.2, б) принимает положение A—Le—C—D. Очевидно, что количество жидкости должно уменьшиться, но количественные оценки целесообразно делать не графически, а с помощью расчетных методик.

ЗАКЛЮЧЕНИЕ

Таким образом, под фазовыми равновесиями понимают сосуществование термодинамически равновесных фаз гетерогенной системы. Фа­зовое равновесие является одним из основных случаев термоди­намического равновесия. Равновесию гетерогенных систем от­вечает:

1. 
   равенство химических потенциалов каждого компонента во всех фазах, что обеспечивает равновесное распределение компонентов между фазами;
   
2. 
   минимальное значение одного из термодинамических потенциалов или максимальное значение энтропии всей систе­мы при данных условиях (для изолированной системы).
   

В ходе работы были изучены четверные системы фазового равновесия, а также диаграммы растворимости и состав - свойство. Так же были приведены некоторые примеры информации, полученной на их основе.

Далее в работе были рассмотрены правило фаз Гиббса, равновесные состояния при фазовых переходах.

Построение диаграмм четырехкомпонентных систем возможно с помощью пространственных моделей, например построения тетраэдра, но изучение таких систем связано с большими трудностями. Изучение систем сплавов с числом компонентов больше четырех еще более сложно. 

Для четверных диаграмм полное графичес­кое изображение практически невозможно, поскольку требуется че­тырехмерное пространство. Из-за сложности графического анализа четверные диаграммы практически не рассматриваются в учебной литературе, хотя они необходимы для корректного анализа многих промышленных сплавов, в частности на основе алюминия.

Список литературы

1. 
   Абрикосов Н.Х. Диаграммы состояния систем на основе меди. Справочник. / Под ред. Н.Х. Абрикосова). — М.: Наука, 1979. — 248.
   
2. 
   Аносов В.Я., Озерова М.И., Фиалков Ю.Я. Основы физико-химического анализа, - М.: Высшая школа 1976.
   
3. 
   Белов Н.А. Компьютерный анализ многокомпонентных диаграмм состояния. — М.: МИСиС, 2003. — 48 с.
   
4. 
   Глазов В.М., Лазарев В.Б., Жаров В.В. Фазовые диаграммы простых веществ - М.: Высшая школа 1980.
   
5. 
   Захаров А.М. Диаграммы состояния двойных и тройных систем. — М.: Металлургия, 1990. — 240 с.
   
6. 
   Захаров А.М. Промышленные сплавы цветных металлов. Фазовый состав и структурные составляющие. — М.: Металлургия, 1980. — 256 с.
   
7. 
   Зломанов В.П. Диаграммы двухкомпонентных систем, - М.: Техносфера 1980.
   
8. 
   Золоторевский В.С., Белов Н.А. Металловедение литейных алюминиевых сплавов. — М.: МИСиС, 2005. — 376 с.
   
9. 
   Кауфман Л., Бернстейн Г., Расчет диаграмм состояния с помощью ЭВМ, пер. с англ. - М.: Мир 1972.
   
10. 
    Кузнецов Г.М. Физика металлов. Раздел: Термодинамика сплавов. — М.: МИСиС. Ч. 2, 1977. — 130 с.
    
11. 
    Мондольфо Л.Ф. Структура и свойства алюминиевых сплавов. — М.: Металлургия, 1979. — 640 с.
    
12. 
    Новик Ф.С. Планирование эксперимента на симплексе при изучении металлических систем. — М.: Машиностроение, 1985. — 256 с.
    
13. 
    Новосёлова А.В. Методы исследования гетерогенных равновесий - М.: Мир 1980.
    
14. 
    Петров Д.А. Четверные системы: новый подход к построению и анализу. — М.: Металлургия, 1991. — 284 с. на Allbest.ru