Предел функции в точке. Предел функции в точке
 Скачать 36.93 Kb. Скачать 36.93 Kb.
|
|
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ 1. Рассмотрим функцию 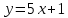 . Проследим как ведёт себя функция, если . Проследим как ведёт себя функция, если 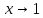 : :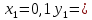 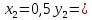 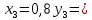   Число _____ называется пределом функции 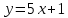 при при 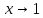 и обозначается и обозначается  … …2. Теоремы о пределах функции. Следствия из теорем. Т1: Если при 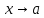 существует предел функции существует предел функции  , то он единственный, т.е. если , то он единственный, т.е. если  , то , то 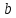 - единственный предел. - единственный предел.Т2: 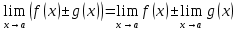 Т3: 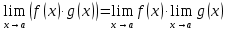 Т4: 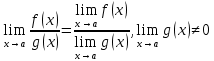 Следствия: 1. 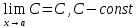 2.  3. 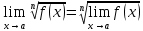 4. 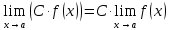 5. 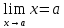 Задание 1 Вычислите предел функции, применяя теоремы о пределах и следствия из них: 1)  2)  3) 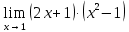 3. Различные случаи вычисления предела частного. 1. Если  . .2. Если 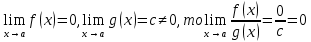 , ,  . .3. Если  - есть неопределенность вида - есть неопределенность вида 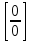 . .Правила исключения неопределенности вида 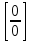 : :1. В большинстве случаев, чтобы исключить неопределённость вида 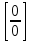 достаточно числитель и знаменатель дроби разложить на множители, а затем сократить на множитель, приводящий к неопределённости (на достаточно числитель и знаменатель дроби разложить на множители, а затем сократить на множитель, приводящий к неопределённости (на 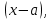 если если 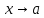 ). ).Например:  Возникла ситуация, когда результат сразу определить невозможно, т.е. возникла неопределенность. Разложим на множители числитель и знаменатель дроби, сократим на множитель Возникла ситуация, когда результат сразу определить невозможно, т.е. возникла неопределенность. Разложим на множители числитель и знаменатель дроби, сократим на множитель 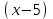 , затем подставим вместо х 5. , затем подставим вместо х 5.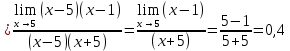 Задание 2 Вычислите предел: 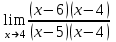 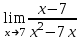  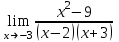 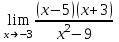  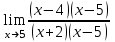 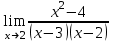  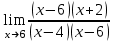 2. Чтобы исключить неопределённость вида 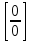 , зависящую от иррациональности, нужно числитель и знаменатель дроби умножить на выражение, сопряженное, содержащему иррациональность, а затем сократить на множитель, приводящий к неопределённости (на , зависящую от иррациональности, нужно числитель и знаменатель дроби умножить на выражение, сопряженное, содержащему иррациональность, а затем сократить на множитель, приводящий к неопределённости (на 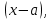 если если 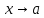 ). ).Например: 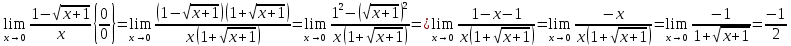 Задание 3 Вычислите предел:   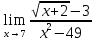 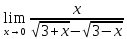 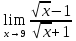 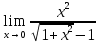 |
