Метрология. Лекц Метрология. Предмет и задачи метрологии

• Название: Предмет и задачи метрологии
• Анкор: Метрология
• Дата: 03.12.2021
• Размер: 1.64 Mb.
• Имя файла: Лекц Метрология.doc
• Тип: Глава; #290110
• страница: 15 из 20

12.2. Метрологические характеристики,

предназначенные для определения

результатов измерений

Функция преобразования F(X). Данная функции нормируется для измерительных преобразователей и приборов с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц входной величины. Она задается в виде формулы, таблицы или графика и используется для определения значений измеряемой величины X в рабочих условиях применения СИ по известному значению информативного параметра его выходного сигнала:

X = F^-1(Y), где F^-1 — функция, обратная функции преобразования; Y — показания средства измерений;

Для стандартизованных СИ серийного производства нормируют номинальную функцию преобразования. Для приборов мелкосерийного производства нормируют индивидуальные функции преобразования. Для стандартизованных СИ, конструктивные особенности которых обуславливают существенный разброс индивидуальных функций преобразования, нормируют пределы (граничные значения), в которых они должны находиться при заданных условиях. Для линейных функций преобразования, проходящих через начало координат, может нормироваться номинальный или индивидуальный коэффициент преобразования.

Значение Y однозначной или значение Y многозначной меры. Для этих характеристик нормируются номинальные или индивидуальные значения. Они используются для устройств, применяемых в качестве мер. Например, у нормального элемента нормируется номинальное значение генерируемой им электродвижущей силы, у кварцевого генератора — значение частоты его колебаний и т.д.

Цена деления шкалы измерительного прибора или многозначной меры. Нормирование цены деления производится для показывающих приборов с равномерной шкалой, функция преобразования которых отображается на именованной шкале. При неравномерной шкале нормируется минимальная цена деления.

Характеристики цифрового кода, используемого в СИ и их элементах. К ним относятся: вид выходного кода, число его разрядов, цена единицы младшего разряда. Эти характеристики нормируются для цифровых приборов.

12.3. Метрологические характеристики

погрешностей средств измерений

Эта группа характеристик описывает погрешности, обусловленные собственными свойствами СИ в нормальных условиях эксплуатации. Суммарное их значение образует основную погрешность СИ.

Характеристики систематической составляющей погрешности. Эти характеристики отражают свойства совокупности СИ данного типа (а не отдельного экземпляра) и описываются либо только значением систематической составляющей _0S, либо его математическим ожиданием М[_0S] и СКО [_0S]. Нормировать последние две величины целесообразно в том случае, если можно пренебречь их изменениями как во времени, так и под влиянием других величин.

Подход к определению систематической составляющей погрешности, регламентированный ГОСТ 8.009—84, несколько отличается от общепринятого. Обычно под систематической погрешностью понимают постоянную или закономерно изменяющуюся детерминированную (неслучайную) величину. Если же из физических соображений ясно, что некоторая составляющая погрешности постоянна или закономерно изменяется, т.е. по определению является систематической, но ее значение неизвестно, а известны лишь пределы, в которых она может находится, то учитывать эту погрешность можно лишь как случайную величину, каким-то образом распределенную в заданных пределах. Природа "случайности" обусловлена не объективными причинами формирования погрешности, а ограниченностью наших знаний и технических возможностей. Поэтому принципы нормирования систематической погрешности должны быть такими же, как и для случайной погрешности.

Такой подход объясняется еще и тем, что характеристики систематической погрешности нормируются для большой совокупности СИ данного типа. При этом погрешности каждого конкретного прибора уже объективно являются частными реализациями случайно распределенной (по экземплярам) величины.

Характеристики систематической составляющей нормируются путем установления пределов допускаемой систематической погрешности _osp = М[_0S]+К_р[_0S], где К_Р — коэффициент, определяемый законом распределения погрешности и принятым значением доверительной вероятности. Могут также нормироваться МО М[_0S] и СКО [_0S]. Эти величины характеризуют разброс систематической составляющей по совокупности экземпляров СИ данного типа и при необходимости позволяют приближенно учесть его.

Характеристики случайной составляющей погрешности. Под случайной составляющей инструментальной погрешности ̊₀ понимается случайная составляющая погрешности СИ, обусловленная только его собственными свойствами. Она представляет собой центрированный случайный процесс и описывается либо СКО [̊₀], либо СКО совместно с нормализованной автокорреляционной функцией г_() или функцией спектральной плотности S().

Характеристики случайной составляющей нормируются путем установления предела допускаемого СКО. Возможно нормирование номинальной нормализованной автокорреляционной функции или номинальной функции спектральной плотности, а также пределов их отклонения от номинальных.

Характеристика случайной составляющей погрешности от гистерезиса. Эта характеристика называется вариацией выходного сигнала СИ. Она представляет собой основание закона распределения случайной составляющей погрешности от гистерезиса. Под случайной составляющей погрешности от гистерезиса ̊_он понимается случайная составляющая погрешности СИ, обусловленная отличием показаний данного экземпляра измерительного прибора от информативного параметра входного сигнала при различных скорости и направлении его изменения.

Характеристика случайной составляющей погрешности от гистерезиса нормируется путем установления предела Н_0р допускаемой вариации выходного сигнала (показания) СИ.

Выбор перечисленных MX основной погрешности в качестве нормируемых сделан [7, 58] на основе математической модели, в которой основная погрешность СИ рассматривается как нестационарный случайный процесс ₀(t):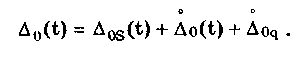

(12.1)

Физический смысл величин, входящих в формулу, следующий. Систематическая составляющая _os(t) включает в себя постоянные и настолько медленно (в том числе и случайно) изменяющиеся во времени погрешности, что их изменением за время проведения измерений можно пренебречь. Частотный спектр погрешности _os(t) лежит в инфранизкочастотной области. Она описывается МО M[_os], СКО [_os] и пределом допускаемых значений _osp. В этих характеристиках не отражена нестационарность погрешности СИ, которая отнесена к систематической составляющей. При необходимости характеристики M[D_os] и [D_os] могут выражаться как функции времени, однако такое представление нецелесообразно в большинстве случаев, так как привело бы к практически не реализуемым методам испытаний.

Составляющая D̊_0q является центрированной случайной величиной, и ее параметры неизменны во времени. Она включает в себя составляющие случайной погрешности, не вошедшие в D_os (t) и D₀(t), например погрешность квантования.

Случайный стационарный эргодический процесс D₀(t) описывает временные изменения погрешности СИ, которые группируются вокруг D_os(t). Погрешность D₀(t), как правило, имеет широкий и неравномерный частотный спектр, в котором целесообразно выделить две типичные составляющие:

D̊_0H(t) — высокочастотную, имеющую такой спектр, что ее интервал корреляции заведомо меньше времени отдельного измерения;

D̊_0L(t)— низкочастотную, имеющую спектр, лежащий между спектрами составляющих D̊_0H(t) и D_os

Удобство такого разделения погрешности D̊₀(t) обусловлено тем, что при оценке характеристик инструментальных составляющих в общем случае необходимо знать автокорреляционную функцию основной погрешности СИ. Очевидно, что подход к определению автокорреляционных функций разных составляющих уравнения (12.1) должен быть различным. Реализации погрешностей D̊_0H(t) и D̊_0q(t) для отдельных измерений всегда некоррелированы, и для них находить автокорреляционные функции не нужно, достаточно определить дисперсию. Аналогично нет необходимости вычислять автокорреляционную функцию систематической составляющей D_os(t), поскольку она практически постоянна в течение измерений. Для составляющей D̊_0L(t) следует определять автокорреляционную функцию.

Учитывая все сказанное выше, уравнение (12.1) можно записать в виде: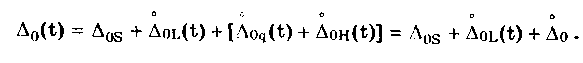

(12.2)

Данная модель включает: D_os — систематическую погрешность, представляющую собой настолько медленно изменяющийся случайный процесс, что в течение продолжительности обычных измерений ее можно считать постоянной. Она описывается пределом допускаемых значений D_osp; D̊_0L(t) коррелированную случайную погрешность, которая описывается автокорреляционной функцией R_() или спектральной плотностью S(). Вместо R_() могут нормироваться нормализованная автокорреляционная функция r() и СКО

[D̊_0L(t)]; D̊₀ — некоррелированную случайную погрешность, которая описывается дисперсией

В рассмотренной модели инструментальной погрешности не учтены гистерезисные явления, вызывающие вариацию показаний. При их учете основная погрешность должна быть записана в виде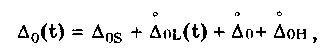

(12.3)

где D̊_0H — случайная составляющая, обусловленная гистерезисом и аналогичными явлениями и подчиняющаяся равномерному закону распределения в пределах некоторого интервала, называемого вариацией. Для этой погрешности нормируется вариация Н_ор. Уравнение (12.3) представляет собой окончательную математическую модель основной погрешности средства измерений.

ГОСТ 8.009—84 допускает при малой случайной погрешности производить нормирование составляющих не отдельно, а в целом погрешности СИ, включая случайную составляющую от гистерезиса.

Если известны нормированные значения характеристик составляющих инструментальной погрешности M[D_os], [D_os], [D̊₀] и Н_ор , то пределы, в которых с заданной вероятностью лежит основная погрешность любого экземпляра СИ данного типа, определяется формулой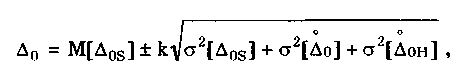



где k — коэффициент, значение которого зависит от доверительной вероятности. При 0,8 < Р < 1 он может быть рассчитан по формуле k = 5(Р - 0,5). Более точные значения коэффициента приведены в руководящем нормативном документе РД 50-453—84.

Дисперсия вариации ²[D̊_0L(t)] = H²_0p /12, так как случайная погрешность от гистерезиса имеет равномерный закон распределения в пределах от 0 до Н_0Р.

Если нормированные значения М[D_os] и [D_os] не заданы, а известно нормированное значение D_osp, то основная погрешность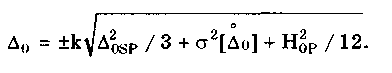



Здесь учтено, что систематическая составляющая погрешности распределена по равномерному закону в пределах ± D_osp.

Использование первой формулы дает более точный результат по сравнению со второй формулой за счет более полного учета статистических свойств систематической составляющей погрешности. Это обуславливается тем, что использование М[D_os] и [ D_os] для расчета не требует знания закона распределения систематической погрешности. При использовании же для расчета величины Адд_р желательно знать закон ее распределения, однако он, как правило, не известен, вследствие чего приходится считать его равномерным. Это и приводит к завышенным расчетным оценкам интервалов для основной погрешности.