Метрология. Лекц Метрология. Предмет и задачи метрологии

• Название: Предмет и задачи метрологии
• Анкор: Метрология
• Дата: 03.12.2021
• Размер: 1.64 Mb.
• Имя файла: Лекц Метрология.doc
• Тип: Глава; #290110
• страница: 2 из 20

1.2. Структура теоретической метрологии

Как отмечалось выше, теоретическая метрология является основным разделом метрологии. Ее структура представлена в виде схемы на рис. 1.1.

Основные представления метрологии. Как и в любой науке, в метрологии необходимо сформулировать основные понятия, термины и постулаты, разработать учение о физических единицах и методологию. Данный раздел особенно важен ввиду того, что в основе отдельных областей измерений лежат специфические представления и в теоретическом плане области развиваются изолированно. При этих условиях недостаточная разработанность основных представлений заставляет решать аналогичные задачи, которые, по сути, являются общими, заново в каждой области.

• Основные понятия и термины. Этот подраздел занимается обобщением и уточнением понятий, сложившихся в отдельных областях измерений с учетом специфики метрологии. Главной задачей является создание единой системы основных понятий метрологии, которая должна служить базой для ее развития. Значение системы понятий определяется значимостью самой теории измерений и тем, что указанная система стимулирует взаимопроникновение методов и результатов, наработанных в отдельных областях измерений.

• Постулаты метрологии. В этом подразделе развивается аксиоматическое построение теоретических основ метрологии, выделяются такие постулаты, на основе которых можно построить содержательную и полную теорию и вывести важные практические следствия.

• Учение о физических величинах. Основной задачей подраздела является построение единой системы ФВ, т.е. выбор основных величин системы и уравнений связи для определения производных величин. Система ФВ служит основой для построения системы единиц ФВ, рациональный выбор которой важен для успешного развития теории и практики метрологического обеспечения.

• Методология измерений. В подразделе разрабатывается научная организация измерительных процессов. Вопросы метрологической методологии являются весьма существенными, поскольку она объединяет области измерений, различные по физической природе измеряемых величин и методам измерений. Это создает определенные трудности при систематизации и объединении понятий, методов и опыта, накопленного в различных областях измерений. К числу основных направлений работ по методологии относятся:

1) переосмысление основ измерительной техники и метрологии в условиях существенного обновления арсенала методов и средств измерений и широкого внедрения микропроцессорной техники;

2) структурный анализ измерительных процессов с системных позиций;

3) разработка принципиально новых подходов к организации процедуры измерений.

Теория единства измерений. (Теория воспроизведения единиц физических величин и передачи их размеров.) Этот раздел традиционно является центральным в теоретической метрологии. Он включает в себя: теорию единиц ФВ, теорию исходных средств измерений (эталонов) и теорию передачи размеров единиц ФВ.

• Теория единиц физических величин. Основная цель подраздела — совершенствование единиц ФВ в рамках существующей системы величин, заключающееся в уточнении и переопределении единиц. Другой задачей является развитие и совершенствование системы единиц ФВ, т.е. изменение состава и определений основных единиц. Работы в этом направлении проводятся постоянно на основе использования новых физических явлений и процессов.

• Теория исходных средств измерений (эталонов). В данном подразделе рассматриваются вопросы создания рациональной системы эталонов единиц ФВ, обеспечивающих требуемый уровень единства измерений. Перспективное направление совершенствования эталонов — переход к эталонам, основанным на стабильных естественных физических процессах. Для эталонов основных единиц принципиально важным является достижение максимально возможного уровня для всех метрологических характеристик.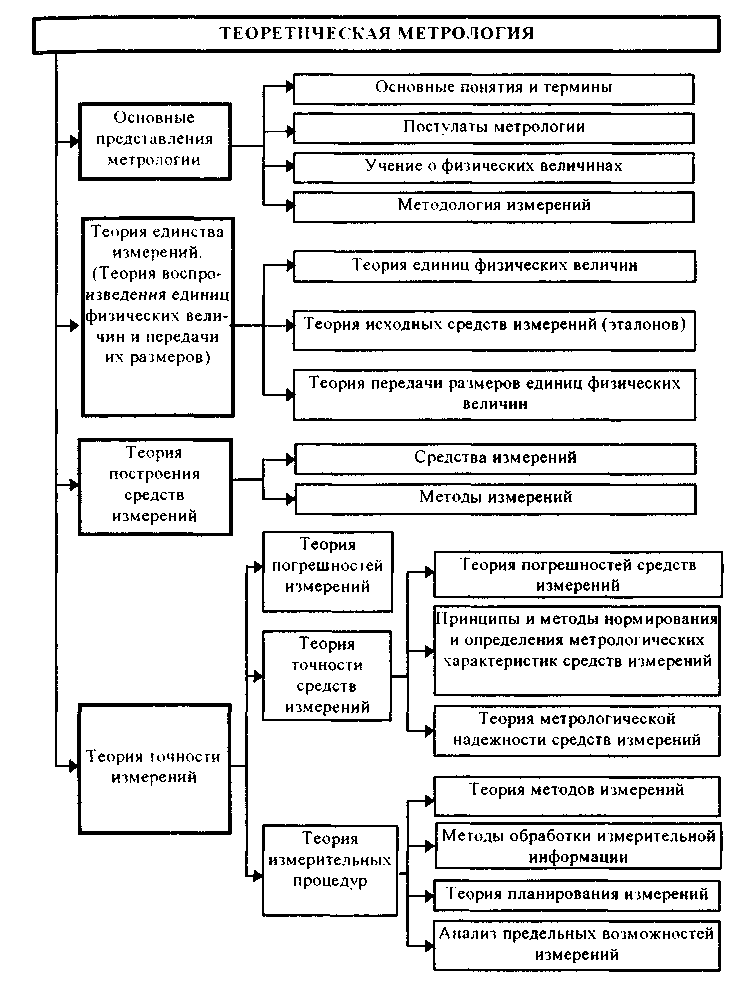


Рис.1.1. Структура теоретической метрологии
• Теория передачи размеров единиц физических величин. Предметом изучения подраздела являются алгоритмы передачи размеров единиц ФВ при централизованном и децентрализованном их воспроизведении. Указанные алгоритмы должны быть основаны как на метрологических, так и на технико-экономических показателях.

Теория построения средств измерений. В разделе обобщается опыт конкретных наук в области построения средств и методов измерений. В последние годы все большее значение приобретают знания, накопленные при разработке электронных СИ электрических и особенно неэлектрических величин. Это связано с бурным развитием микропроцессорной и вычислительной техники и ее активным использованием при построении СИ, что открывает новые возможности при обработке результатов. Важной задачей является разработка новых и совершенствование известных измерительных преобразователей.

Теория точности измерений. В данном разделе метрологии обобщены методы, развиваемые в конкретных областях измерений. Он состоит их трех подразделов: теории погрешностей, теории точности средств измерений и теории измерительных процедур.

• Теория погрешностей. Этот подраздел является одним из центральных в метрологии, поскольку результаты измерений объективны настолько, насколько правильно оценены их погрешности. Предметом теории погрешностей является классификация погрешностей измерений, изучение и описание их свойств. Сложившееся исторически деление погрешностей на случайные и систематические, хотя и вызывает справедливые нарекания, тем не менее продолжает активно использоваться в метрологии. Как известная альтернатива такому делению погрешностей может рассматриваться развиваемое в последнее время описание погрешностей на основе теории нестационарных случайных процессов. Важной частью подраздела является теория суммирования погрешностей.

• Теория точности средств измерений. Подраздел включает: теорию погрешностей средств измерений, принципы и методы определения и нормирования метрологических характеристик средств измерений, методы анализа их метрологической надежности.

Теория погрешностей средств измерений наиболее детально разработана в метрологии. Значительные знания накоплены и в конкретных областях измерений, на их основе развиты общие методы расчета погрешностей СИ. В настоящее время в связи с усложнением СИ, развитием микропроцессорных измерительных устройств актуальной стала задача по расчету погрешностей цифровых СИ вообще и измерительных систем и измерительно-вычислительных комплексов в частности.

Принципы, и методы определения и нормирования метрологических характеристик СИ достаточно хорошо разработаны. Однако они требуют модификации с учетом специфики метрологии и в первую очередь тесной связи определения метрологических характеристик СИ с их нормированием. К числу не до конца решенных задач следует отнести определение динамических характеристик СИ и градуировочных характеристик первичных измерительных преобразователей. По мере совершенствования средств обработки электрических измерительных сигналов наиболее существенные метрологические проблемы концентрируются вокруг выбора первичного преобразователя. Ввиду разнообразия принципов действия и типов СИ, а также повышения требуемой точности измерений появляется проблема выбора нормируемых метрологических характеристик СИ.

Теория метрологической надежности средств измерений по своей целевой направленности связана с общей теорией надежности. Однако специфика метрологических отказов и прежде всего непостоянство во времени их интенсивности делают невозможным автоматическое перенесение методов классической теории надежности в теорию метрологической надежности. Необходима разработка специальных методов анализа метрологической надежности СИ.

• Теория измерительных процедур. Повышение сложности измерительных задач, постоянный рост требований к точности измерений, усложнение методов и средств измерений обуславливают проведение исследований, направленных на обеспечение рациональной организации и эффективного выполнения измерений. При этом главную роль играет анализ измерений как совокупности взаимосвязанных этапов, т.е. как процедуры. Подраздел включает теорию методов измерений; методы обработки измерительной информации; теорию планирования измерений; анализ предельных возможностей измерений.

Теория методов измерений — подраздел, посвященный разработке новых методов измерений и модификации существующих, что связано с ростом требований к точности измерений, диапазонам, быстродействию, условиям проведения измерений. С помощью современных средств измерений реализуются сложные совокупности классических методов. Поэтому остается актуальной традиционная задача совершенствования существующих методов и исследования их потенциальных возможностей с учетом условий реализации.

Методы обработки измерительной информации, используемые в метрологии, основываются на методах, которые заимствуются из математики, физики и других дисциплин. В связи с этим актуальна задача обоснованности выбора и применения- того или иного способа обработки измерительной информации и соответствия требуемых исходных данных теоретического способа тем, которыми реально располагает экспериментатор.

Теория планирования измерений — область метрологии, которая весьма активно развивается. К числу ее основных задач относятся уточнение метрологического содержания задач планирования измерений и обоснование заимствований математических методов из общей теории планирования эксперимента.

Анализ предельных возможностей измерений на данном уровне развития науки и техники позволяет решить такую главную задачу, как исследование предельной точности измерений при помощи конкретных типов или экземпляров средств измерений.
Контрольные вопросы
1. Обоснуйте важность теоретической метрологии.

2. Что изучает теоретическая метрология?

3. Каково место метрологии среди других наук?

4. Что такое измерение? Приведите примеры измерений, постоянно встречающихся в повседневной жизни.

5. В чем заключается значимость метрологии?

6. Перечислите, из каких основных разделов состоит теоретическая метрология. Какие задачи в них решаются?

7. Сформулируйте основные этапы развития метрологии.

8. Какие основные метрологические учреждения существуют в нашей стране? Какова их сфера деятельности?

3.3. Международная система единиц (система СИ)

Единая международная система единиц (система СИ) была принята XI Генеральной конференцией по мерам и весам в 1960 г. На территории нашей страны система единиц СИ действует с 1 января 1982 г. в соответствии ГОСТ 8.417-81 "ГСИ. Единицы физических величин". Система СИ возникла не на пустом месте и является логическим развитием предшествовавших ей систем единиц СГС и МКГСС и др.

В настоящее время широко применяются две системы единиц: СИ и СГС (симметричная, или гауссова). Система СГС существует более 100 лет и до сих пор используется в точных науках — физике, астрономии. Однако ее все более теснит система СИ - единственная система единиц ФВ, которая принята и используется в большинстве стран мира. Это обусловлено ее достоинствами и преимуществами перед другими системами единиц, к которым относятся:

• универсальность, т.е. охват всех областей науки и техники;

• унификация всех областей и видов измерений;

• когерентность величин;

• возможность воспроизведения единиц с высокой точностью в соответствии с их определением;

• упрощение записи формул в физике, химии, а также в технических науках в связи с отсутствием переводных коэффициентов;

• уменьшение числа допускаемых единиц;

• единая система образования кратных и дольных единиц, имеющих собственные наименования;

• облегчение педагогического процесса в средней и высшей школах, так как отпадает необходимость в изучении множества систем единиц и внесистемных единиц;

• лучшее взаимопонимание при развитии научно-технических и экономических связей между различными странами.

3.4. Воспроизведение единиц физических величин

и передача их размеров

3.4.1. Понятие о единстве измерений

При проведении измерений необходимо обеспечить их единство. Под единством измерений понимается характеристика качества измерений, заключающаяся в том, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам воспроизведенных величин, а погрешности результатов измерений известны с заданной вероятностью и не выходят за установленные пределы. Понятие "единство измерений" довольно емкое. Оно охватывает важнейшие задачи метрологии: унификацию единиц ФВ, разработку систем воспроизведения величин и передачи их размеров рабочим средствам измерений с установленной точностью и ряд других вопросов. Единство должно обеспечиваться при любой точности, необходимой науке и технике. На достижение и поддержание на должном уровне единства измерений направлена деятельность государственных и ведомственных метрологических служб, проводимая в соответствии с установленными правилами, требованиями и нормами. На государственном уровне деятельность по обеспечению единства измерений регламентируется стандартами Государственной системы обеспечения единства измерений (ГСИ) или нормативными документами органов метрологической службы.

Для обеспечения единства измерений необходима тождественность единиц, в которых проградуированы все существующие СИ одной и той же величины. Это достигается путем точного воспроизведения и хранения в специализированных учреждениях установленных единиц ФВ и передачи их размеров применяемым СИ.

Воспроизведение единицы физической величины — это совокупность операций по материализации единицы ФВ с наивысшей в стране точностью посредством государственного эталона или исходного образцового СИ. Различают воспроизведение основной и производной единиц.

Воспроизведение основной единицы — это воспроизведение единицы путем создания фиксированной по размеру ФВ в соответствии с определением единицы. Оно осуществляется с помощью государственных первичных эталонов. Например, единица массы — 1 килограмм (точно) воспроизведена в виде платиноиридиевой гири, хранимой в Международном бюро мер и весов в качестве международного эталона килограмма. Розданные другим странам эталоны имеют номинальное значение 1 кг. На основании последних международных сличений (1979) платиноиридиевая гиря, входящая в состав Государственного эталона РФ, имеет массу 1,000000087 кг.

Воспроизведение производной единицы — это определение значения ФВ в указанных единицах на основании косвенных измерений других величин, функционально связанных с измеряемой. Так, воспроизведение единицы силы — Ньютона — осуществляется на основании известного уравнения механики F = mg, где m — масса тела; g — ускорение свободного падения.

Передача размера единицы — это приведение размера единицы ФВ, хранимой поверяемым средством измерений, к размеру единицы, воспроизводимой или хранимой эталоном, осуществляемое при их поверке или калибровке. Размер единицы передается "сверху вниз"— от более точных СИ к менее точным.

Хранение единицы — совокупность операций, обеспечивающая неизменность во времени размера единицы, присущего данному СИ. Хранение эталона единицы ФВ предполагает проведение взаимосвязанных операций, позволяющих поддерживать метрологические характеристики эталона в установленных пределах. При хранении первичного эталона выполняются регулярные его исследования, включая сличения с национальными эталонами других стран с целью повышения точности воспроизведения единицы и совершенствования методов передачи ее размера.

3.4.2. Эталоны, единиц физических величин

Эталон — средство измерений (или комплекс СИ), предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера нижестоящим по поверочной схеме СИ и утвержденное в качестве эталона в установленном порядке. Классификация, назначение и общие требования к созданию, хранению и применению эталонов устанавливает ГОСТ 8.057-80 "ГСИ. Эталоны единиц физических величин. Основные положения".

Перечень эталонов не повторяет перечня ФВ. Для ряда единиц эталоны не создаются из-за того, что нет возможности непосредственно сравнивать соответствующие ФВ, например, нет эталона площади. Не создаются эталоны и в том случае, когда единица ФВ воспроизводится с достаточной точностью на основе сравнительно простых средств измерений других ФВ.

Конструкция эталона, его физические свойства и способ воспроизведения единицы определяются ФВ, единица которой воспроизводится, и уровнем развития измерительной техники в данной области измерений. Эталон должен обладать по крайней мере тремя взамосвязанными свойствами: неизменностью, воспроизводимостью и сличаемостью.

Неизменность — свойство эталона удерживать неизменным размер воспроизводимой им единицы в течение длительного интервала времени, при этом все изменения, зависящие от внешних условий, должны быть строго определенными функциями величин, доступных точному измерению. Реализация этих требований привела к идее создания "естественных" эталонов различных величин, основанных на физических постоянных.

Воспроизводимость — возможность воспроизведения единицы ФВ (на основе ее теоретического определения) с наименьшей погрешностью для существующего уровня развития измерительной техники. Это достигается путем постоянного исследования эталона в целях определения систематических погрешностей и их исключения путем введения соответствующих поправок.

Сличаемостъ — возможность обеспечения сличения с эталоном других СИ, нижестоящих по поверочной схеме, в первую очередь вторичных эталонов, с наивысшей точностью для существующего уровня развития техники измерения. Это свойство предполагает, что эталоны по своему устройству и действию не вносят каких-либо искажений в результаты сличений и сами не претерпевают изменений при проведении сличений.

Различают следующие виды эталонов:

• первичный — обеспечивает воспроизведение и хранение единицы с наивысшей в стране (по сравнению с другими эталонами той же величины) точностью. Первичные эталоны — это уникальные СИ, часто представляющие собой сложнейшие измерительные комплексы, созданные с учетом новейших достижений науки и техники. Они составляют основу государственной системы обеспечения единства измерений;

• специальный — обеспечивает воспроизведение единицы в особых условиях, в которых прямая передача размера единицы от первичного эталона с требуемой точностью не осуществима, и служит для этих условий первичным эталоном;

• государственный— это первичный или специальный эталон, официально утвержденный в качестве исходного для страны. Утверждение проводит главный метрологический орган страны. Государственные эталоны создаются, хранятся и применяются центральными метрологическими научными институтами страны. Точность воспроизведения единицы должна соответствовать уровню лучших мировых достижений и удовлетворять потребностям науки и техники. В состав государственных эталонов включаются СИ, с помощью которых воспроизводят и (или) хранят единицу ФВ, контролируют условия измерений и неизменность воспроизводимого или хранимого размера единицы, осуществляют передачу размера единицы. Государственные эталоны подлежат периодическим сличениями с государственными эталонами других стран;

• вторичный — хранит размер единицы, полученной путем сличения с первичным эталоном соответствующей ФВ. Вторичные эталоны являются частью подчиненных средств хранения единиц и передали их размеров, создаются и утверждаются в тех случаях, когда это необходимо для организации поверочных работ, а также для обеспечения сохранности и наименьшего износа государственного эталона. В состав вторичных эталонов включаются СИ, с помощью которых хранят единицу ФВ, контролируют условия хранения и передают размер единицы.

По своему метрологическому назначению вторичные эталоны делятся на следующие:

• эталон-копия — предназначен для передачи размера единицы рабочим эталонам. Он создается в случае необходимости проведения большого числа поверочных работ с целью предохранения первичного или специального эталона от преждевременного износа. Эталон-копия представляют собой копию государственного эталона только по метрологическому назначению, поэтому он не всегда является его физической копией;

• эталон сравнения — применяется для сличения эталонов, которые по тем или иным причинам не могут быть непосредственно сличаемы друг с другом;

• эталон-свидетель — предназначен для проверки сохранности и неизменности государственного эталона и замены его в случае порчи или утраты. В настоящее время только эталон килограмма имеет эталон-свидетель. Его основное назначение — обеспечивать возможность контролироля постоянства основного эталона;

• рабочий эталон — применяется для передачи размера единицы рабочим средствам измерений. Это самые распространенные эталоны. С целью повышения точности измерений ФВ рабочие эталоны применяются во многих территориальных метрологических органах и лабораториях министерств и ведомств.

Способы выражения погрешностей эталонов устанавливает ГОСТ 8.381-80 "ГСИ. Эталоны, Способы выражения погрешностей". Погрешности государственных первичных и специальных эталонов характеризуются неисключенной систематической погрешностью, случайной погрешностью и нестабильностью. Неисключенная систематическая погрешность описывается границами, в которых она находится. Случайная погрешность определяется средним квадратичес-ким отклонением (СКО) результата измерений при воспроизведении единицы с указанием числа независимых измерений. Нестабильность эталона задается изменением размера единицы, воспроизводимой или хранимой эталоном, за определенный промежуток времени.

Оценки погрешностей вторичных эталонов характеризуются отклонением размеров хранимых ими единиц от размера единицы, воспроизводимой первичным эталоном. Для вторичного эталона указывается суммарная погрешность, включающая случайные погрешности сличаемых эталонов и погрешности передачи размеров единицы от первичного (или более точного) эталона, а также нестабильность самого вторичного эталона. Суммарная погрешность вторичного эталона характеризуется либо СКО результата измерений при его сличении с первичным эталоном или вышестоящим по поверочной схеме вторичным эталоном, либо доверительной границей погрешности с доверительной вероятностью 0,99.

Передача размеров единиц ФВ от эталонов рабочим мерам и измерительным приборам осуществляется с помощью рабочих эталонов. До недавнего времени в нашей стране вместо термина "рабочие эталоны" использовался термин "образцовые средства измерений", который в большинстве других стран не применяется.

Рабочие эталоны при необходимости подразделяются на разряды 1, 2 и т.д., определяющие порядок их соподчинения в соответствии с поверочной схемой. Для различных видов измерений устанавливается, исходя из требований практики, различное число разрядов рабочих эталонов, определяемых стандартами на поверочные схемы для данного вида измерений.

3.4.3. Поверочные схемы

Обеспечение правильной передачи размера единиц ФВ во всех звеньях метрологической цепи осуществляется посредством поверочных схем. Поверочная схема — это нормативный документ, который устанавливает соподчинение средств измерений, участвующих в передаче размера единицы от эталона к рабочим СИ с указанием методов и погрешности, и утвержден в установленном порядке. Основные положения о поверочных схема приведены в ГОСТ 8.061-80 "ГСИ. Поверочные схемы. Содержание и построение". Поверочные схемы делятся на государственные, ведомственные и локальные.

• Государственная поверочная схема распространяется на все СИ данной ФВ, имеющиеся в стране. Она разрабатывается в виде государственного стандарта, состоящего из чертежа поверочной схемы и текстовой части, содержащей пояснения к чертежу.

• Ведомственная поверочная схема распространяется на СИ данной ФВ, подлежащие ведомственной поверке.

• Локальная поверочная схема распространяется на СИ данной ФВ, подлежащие поверке в отдельном органе метрологической службы.

Ведомственные поверочные схемы не должны противоречить государственным поверочным схемам для СИ одних и тех же ФВ. Они могут быть составлены при отсутствии государственной поверочной схемы. В них допускается указывать конкретные типы (экземпляры) СИ. Ведомственная и локальная поверочные схемы оформляют в виде чертежа, элементы которого приведены на рис. 3.1.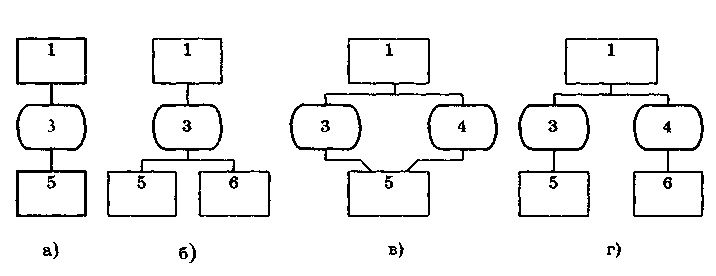



Рис. 3.1. Элементы графического изображения поверочных схем:

передача размера: а) от эталона 1 к объекту 5 методом 3; б) от эталона 1 к объектам поверки 5 и 6 методом 3; в) от эталона 1 к объекту поверки 5 методом 3 или 4; г) от эталона 1 к объекту поверки 5 методом 3 и объекту поверки 6 методом 4
Поверочная схема устанавливает передачу размера единиц одной или нескольких взаимосвязанных величин. Она должна включать не менее двух ступеней передачи размера. Поверочную схему для СИ одной и той же величины, существенно отличающихся по диапазонам измерений, условиям применения и методам поверки, а также для СИ нескольких ФВ допускается подразделять на части. На чертежах поверочной схемы должны быть указаны:

• наименования СИ и методов поверки;

• номинальные значения ФВ или их диапазоны;

• допускаемые значения погрешностей СИ;

• допускаемые значения погрешностей методов поверки. Правила расчета параметров поверочных схем и оформления чертежей поверочных схем приведены в ГОСТ 8.061-80 "ГСИ. Поверочные схемы. Содержание и построение" и в рекомендациях МИ 83—76 "Методика определения параметров поверочных схем".

Контрольные вопросы
1. Сформулируйте определение единицы физической величины. Приведите примеры единиц физических величин, относящихся к механике, магнетизму и оптике.

2. Что такое размерность физической величины? Запишите размерность следующих физических величин: паскаля, генри, ома, фарады и вольта.

3. Дайте определения системы физических величин и системы единиц физических величин. Приведите примеры основных и производных физических величин и единиц?

4. Сформулируйте основные принципы построения систем единиц физических величин.

5. Назовите производные единицы системы СИ, имеющие специальное название.

6. Какие внесистемные единицы допущены к применению наравне с единицами системы СИ?

7. Назовите приведенные значения физических величин, используя кратные и дольные приставки: 5,310¹³ Ом; 10,410¹³ Гц; 2,5610⁷ Па; 4,6710⁴ Ом; 0,067 м; 0,0098 с; 7,6510^-3 с; 6,3410^-6 Ф; 45,610^-9 с; 12,310^-13 Ф.

8. В чем заключается единство измерений?

9. Что такое эталон единицы физической величины? Какие типы эталонов вам известны?

10. Что такое поверочная схема и для чего она предназначена? Какие существуют виды поверочных схем?

11. Что такое поверка средств измерений и какими способами она может проводиться?

12. Для чего используются стандартные образцы? Назовите их метрологические характеристики. Приведите пример стандартных образцов.

13. Расскажите о государственных эталонах основных единиц системы СИ. Проанализируйте каждый из них с точки зрения неизменности во времени, воспроизводимости и неуничтожимости.

Глава 4. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ

ПОГРЕШНОСТЕЙ

4.1. Классификация погрешностей

Качество средств и результатов измерений принято характеризовать, указывая их погрешности. Введение понятия "погрешность" требует определения и четкого разграничения трех понятий: истинного и действительного значений измеряемой физической величины и результата измерения. Истинное значение физической величины — это значение, идеальным образом отражающее свойство данного объекта как в количественном, так и в качественном отношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить ее в виде числовых значений. На практике это абстрактное понятие приходится заменять понятием "действительное значение". Действительное значение физической величины. — значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Результат измерения представляет собой приближенную оценку истинного значения величины, найденную путем измерения.

Понятие "погрешность" — одно из центральных в метрологии, где используются понятия "погрешность результата измерения" и "погрешность средства измерения". Погрешность результата измерения — это разница между результатом измерения X и истинным (или действительным) значением Q измеряемой величины: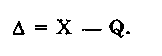

(4.1)

Она указывает границы неопределенности значения измеряемой величины. Погрешность средства измерения — разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность результатов измерений, проводимых данным средством.

Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам.

По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи).

Заметим, что из приведенного выше определения погрешности никак не следует, что она должна состоять из каких-либо составляющих. Деление погрешности на составляющие было введено для удобства обработки результатов измерений исходя из характера их проявления, В процессе формирования метрологии было обнаружено, что погрешность не является постоянной величиной. Путем элементарного анализа установлено, что одна ее часть проявляется как постоянная величина, а другая — изменяется непредсказуемо. Эти части назвали систематической и случайной погрешностями.

Как будет показано в разд. 4.3, изменение погрешности во времени представляет собой нестационарный случайный процесс. Разделение погрешности на систематическую, прогрессирующую и случайную составляющие представляет собой попытку описать различные участки частотного спектра этого широкополосного процесса: инфранизкочастотный, низкочастотный и высокочастотный.

Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях. В появлении таких погрешностей (рис. 4.1) не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.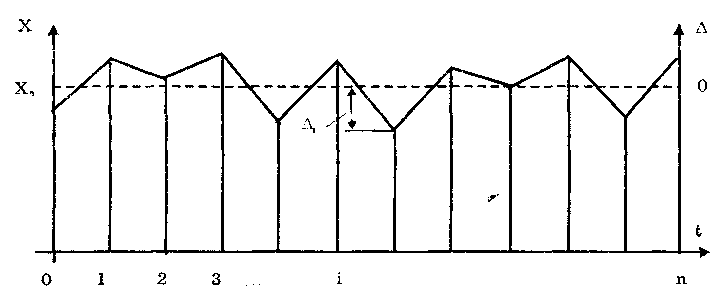



Рис. 4.1 . Изменение случайной погрешности от измерения к измерению
В отличие от систематических случайные погрешности нельзя исключить из результатов измерений путем введения поправки, однако их можно существенно уменьшить путем увеличения числа наблюдений. Поэтому для получения результата, минимально отличающегося от истинного значения измеряемой величины, проводят многократные измерения требуемой величины с последующей математической обработкой экспериментальных данных.

Систематическая погрешность — составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ. Постоянная и переменная систематические погрешности показаны на рис. 4.2. Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.

Прогрессирующая (дрейфовая) погрешность — это непредсказуемая погрешность, медленно меняющаяся во времени. Впервые это понятие было введено в монографии М.Ф. Маликова "Основы метрологии" [17], изданной в 1949 г. Отличительные особенности прогрессирующих погрешностей:

• они могут быть скорректированы поправками только в данный момент времени, а далее вновь непредсказуемо изменяются;

• изменения прогрессирующих погрешностей во времени — нестационарный случайный процесс, и поэтому в рамках хорошо разработанной теории стационарных случайных процессов они могут быть описаны лишь с известными оговорками.

Прогрессирующая погрешность — это понятие, специфичное для нестационарного случайного процесса изменения погрешности во времени, оно не может быть сведено к понятиям случайной и систематической погрешностей. Последние характерны лишь для стационарных случайных процессов. Прогрессирующая погрешность может возникнуть вследствие как непостоянства во времени текущего математического ожидания нестационарного случайного процесса, так и изменения во времени его дисперсии или формы закона распределения.

Грубая погрешность (промах) — это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Они, как правило, возникают из-за ошибок или неправильных действий оператора (его психофизиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов или сбоев в их работе и др.). Возможной причиной возникновения промахов также могут быть кратковременные резкие изменения условий проведения измерений. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают. Однако чаще всего промахи выявляют только при окончательной обработке результатов измерений с помощью специальных критериев, которые рассмотрены в гл. 7.

По способу выражения различают абсолютную, относительную и приведенную погрешности.

Абсолютная погрешность описывается формулой (4.1) и выражается в единицах измеряемой величины. Однако она не может в полной мере служить показателем точности измерений, так как одно и то же ее значение, например, Д = 0,05 мм при X = 100 мм соответствует достаточно высокой точности измерений, а при X — 1 мм — низкой. Поэтому и вводится понятие относительной погрешности. Относительная погрешность — это отношение абсолютной погрешности измерения к истинному значению измеряемой величины:

(4.2)

Эта наглядная характеристика точности результата измерения не годится для нормирования погрешности СИ, так как при изменении значений Q принимает различные значения вплоть до бесконечности при Q = 0. В связи с этим для указания и нормирования погрешности СИ используется еще одна разновидность погрешности — приведенная.

Приведенная погрешность — это относительная погрешность, в которой абсолютная погрешность СИ отнесена к условно принятому значению Q_N, постоянному во всем диапазоне измерений или его части: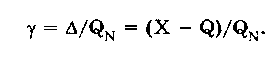

(4.3)

Условно принятое значение Q_N называют нормирующим. Чаще всего за него принимают верхний предел измерений данного СИ, применительно к которым и используется главным образом понятие "приведенная погрешность".

В зависимости от места возникновения различают инструментальные, методические и субъективные погрешности.

Инструментальная погрешность обусловлена погрешностью применяемого СИ. Иногда эту погрешность называют аппаратурной.

Методическая погрешность измерения обусловлена:

• отличием принятой модели объекта измерения от модели, адекватно описывающей его свойство, которое определяется путем измерения;

• влиянием способов применения СИ. Это имеет место, например, при измерении напряжения вольтметром с конечным значением внутреннего сопротивления. В данном случае вольтметр шунтирует участок цепи, на котором измеряется напряжение, и оно оказывается меньше, чем было до присоединения вольтметра;

• влиянием алгоритмов (формул), по которым производятся вычисления результатов измерений;

• влиянием других факторов, не связанных со свойствами используемых средств измерения.

Отличительной особенностью методических погрешностей является то, что они не могут быть указаны в нормативно-технической документации на используемое СИ, поскольку от него не зависят, а должны определяться оператором в каждом конкретном случае. В связи с этим оператор должен четко различать фактически измеряемую им величину и величину, подлежащую измерению.

Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов. Они вызываются состоянием оператора, его положением во время работы, несовершенством органов чувств, эргономическими свойствами СИ. Характеристики личной погрешности определяют на основе нормированной номинальной цены деления шкалы измерительного прибора (или диаграммной бумаги регистрирующего прибора) с учетом способности "среднего оператора" к интерполяции в пределах деления шкалы.

По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности (рис. 4.4):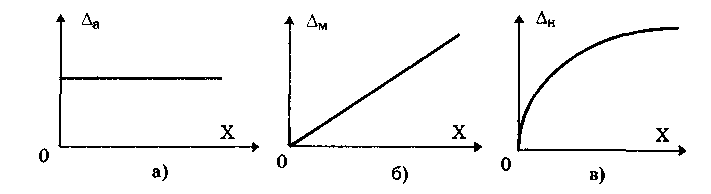


Рис. 4.4. Аддитивная (а), мультипликативная (б) и нелинейная (в)

погрешности
• аддитивные _а, не зависящие от измеряемой величины;

• мультипликативные _м, которые прямо пропорциональны измеряемой величине;

• нелинейные _н, имеющие нелинейную зависимость от измеряемой величины.

Эти погрешности применяют в основном для описания метрологических характеристик СИ. Разделение погрешностей на аддитивные, мультипликативные и нелинейные весьма существенно при решении вопроса о нормировании и математическом описании погрешностей СИ.

Примеры аддитивных погрешностей — от постоянного груза на чашке весов, от неточной установки на нуль стрелки прибора перед измерением, от термо-ЭДС в цепях постоянного тока. Причинами возникновения мультипликативных погрешностей могут быть: изменение коэффициента усиления усилителя, изменение жесткости мембраны датчика манометра или пружины прибора, изменение опорного напряжения в цифровом вольтметре.

По влиянию внешних условий различают основную и дополнительную погрешности СИ. Основной называется погрешность СИ, определяемая в нормальных условиях его применения. Для каждого СИ в нормативно-технических документах оговариваются условия эксплуатации — совокупность влияющих величин (температура окружающей среды, влажность, давление, напряжение и частота питающей сети и др.), при которых нормируется его погрешность. Дополнительной называется погрешность СИ, возникающая вследствие отклонения какой-либо из влияющих величин.

В зависимости от влияния характера изменения измеряемых величин погрешности СИ делят на статические и динамические. Статическая погрешность — это погрешность СИ применяемого для измерения ФВ, принимаемой за неизменную. Динамической называется погрешность СИ, возникающая дополнительно при измерении переменной ФВ и обусловленная несоответствием его реакции на скорость (частоту) изменения измеряемого сигнала.

4.2. Принципы оценивания погрешностей

Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Точность результата измерения характеризуется погрешностью. Погрешность измерения описывается определенной математической моделью, выбор которой обуславливается имеющимися априорными сведениями об источниках погрешности, а также данными, полученными в ходе измерений. С помощью выбранной модели определяются характеристики и параметры погрешности, используемые для количественного выражения тех или иных ее свойств.

Характеристики погрешности принято делить на точечные и интервальные. К точечным относятся СКО случайной погрешности и предел сверху для модуля систематической погрешности, к интервальным — границы неопределенности результата измерения. Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называются предельными (безусловными) интервалами.

В основу выбора оценок погрешностей положен ряд принципов. Во-первых, оцениваются отдельные характеристики и параметры выбранной модели погрешности. Во-вторых, оценки погрешности определяют приближенно, с точностью, согласованной с целью измерения. В-третьих, погрешности оцениваются сверху, поэтому погрешность лучше преувеличить, чем преуменьшить, так как в первом случае снижается качество измерений, а во втором — возможно полное обесценивание результатов всего измерения. В-четвертых, поскольку стремятся получить реалистические значения оценки погрешности результата измерения, т.е. не слишком завышенные и не слишком заниженные, точность измерений должна соответствовать цели измерения. Излишняя точность ведет к неоправданному расходу средств и времени.

Оценивание погрешностей может проводится до (априорное) и после (апостериорное) измерения. Априорное оценивание — это проверка возможности обеспечить требуемую точность измерений, проводимых в заданных условиях выбранным методом с помощью конкретных СИ. Оно проводится в случаях:

• нормирования метрологических характеристик СИ;

• разработки методик выполнения измерений;

• выбора средств измерений для решения конкретной измерительной задачи;

• подготовки измерений, проводимых с помощью конкретного СИ.

Апостериорную оценку проводят в тех случаях, когда априорная оценка неудовлетворительна или получена на основе типовых метрологических характеристик, а требуется учесть индивидуальные свойства используемого СИ. Такую оценку следует рассматривать как коррекцию априорных оценок.

4.5. Правила округления результатов измерений

Поскольку погрешности измерений определяют лишь зону неопределенности результатов, их не требуется знать очень точно. В окончательной записи погрешность измерения принято выражать числом с одним или двумя значащими цифрами, Эмпирически были установлены следующие правила округления рассчитанного значения погрешности и полученного результата измерения.

1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной — если первая цифра равна 3 или более.

2. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности.

3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.

4. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.

5. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная.

6. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.

Если руководствоваться этими правилами округления, то количество значащих цифр в числовом значении результата измерений дает возможность ориентировочно судить о точности измерения. Это связано с тем, что предельная погрешность, обусловленная округлением, равна половине единицы последнего разряда числового значения результата измерения.

Для оценки влияния округления результата измерения Y представим его в виде

(4.4)

где А₁ ..., А_s— десятичные цифры и старшая цифра A₁ ≠ 0; R, P, S — целые числа, причем R - Р = S - 1.

Абсолютная погрешность, обусловленная округлением,  = 0,510^P. В качестве оценки относительной предельной погрешности округления рекомендуется [4] принять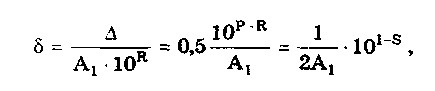



поскольку деление абсолютной погрешности лишь на первый член суммы (4.4) ведет к увеличению числового значения оценки погрешности. Поскольку значения A₁ могут находиться в пределах от 1 до 9, то при одной значащей цифре (S = 1) предельная погрешность округления может находится в пределах от 6 до 50%. При двух значащих цифрах она составит от 0,6 до 5%, при трех — от 0,06 до 0,5%.

Оцененные границы погрешности округления характеризуют влияние округления на точность результата измерения. Кроме того, эти данные позволяют ориентироваться в минимально необходимом для записи результата измерений числе значащих цифр при его заданной точности.
Контрольные вопросы
1. Перечислите возможные проявления погрешностей.

2. Назовите признаки, по которым классифицируются погрешности.

3. Сформулируйте свойства случайной, систематической и прогрессирующей составляющих погрешности измерений.

4. Приведите известные вам примеры методических погрешностей.

5. В чем заключаются принципы оценивания погрешностей?

6. Расскажите о математических моделях погрешности измерения.

7. Какие характеристики погрешностей вам известны?

8. Перечислите правила округления результатов измерений.

9. Каким образом ориентировочно оценить погрешность результата измерения по числу его значащих цифр?