Метрология. Лекц Метрология. Предмет и задачи метрологии
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
Глава 5. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ5.1. Систематические погрешности и ихклассификацияВ настоящее время, особенно после введения одного из основополагающих метрологических стандартов — ГОСТ 8.009-84 ТСИ. Нормируемые метрологические характеристики средств измерений", понятие "систематическая погрешность" несколько изменилось по отношению к определению, данному ГОСТ 16263-70 ТСИ. Метрология. Термины и определения". Систематическая погрешность считается специфической, "вырожденной" случайной величиной, обладающей некоторыми, но не всеми свойствами случайной величины, изучаемой в теории вероятностей и математической статистике. Свойства систематической погрешности, которые необходимо учитывать при объединении составляющих погрешности, отражаются такими же характеристиками, что и свойства "настоящих" случайных величин — дисперсией (СКО) и коэффициентом взаимной корреляции. Систематическая погрешность представляет собой определенную функцию влияющих факторов, состав которых зависит от физических, конструктивных и технологических особенностей СИ, условий их применения, а также индивидуальных качеств наблюдателя. В метрологической практике при оценке систематических погрешностей должно учитываться влияние следующих основных факторов: 1. Объект измерения. Перед измерением он должен быть достаточно хорошо изучен с целью корректного выбора его модели. Чем полнее модель соответствует исследуемому объекту, тем точнее могут быть получены результаты измерения. Например, кривизна земной поверхности может не учитываться при измерении площади сельскохозяйственных угодий, так как она не вносит ощутимой погрешности, однако при измерении площади океанов ею пренебрегать уже нельзя. 2. Субъект измерения. Его вклад в погрешность измерения необходимо уменьшать путем подбора операторов высокой квалификации и соблюдения требований эргономики при разработке СИ. 3. Метод и средство измерений. Чрезвычайно важен их правильный выбор, который производится на основе априорной информации об объекте измерения. Чем больше априорной информации, тем точнее может быть проведено измерение. Основной вклад в систематическую погрешность вносит, как правило, методическая погрешность. 4. Условия измерения. Обеспечение и стабилизация нормальных условий являются необходимыми требованиями для минимизации дополнительной погрешности, которая по своей природе, как правило, является систематической. Систематические погрешности принято классифицировать по двум признакам. По характеру изменения во времени они делятся на постоянные и переменные. Постоянными называются такие погрешности измерения, которые остаются неизменными в течение всей серии измерений. Например, погрешность от того, что неправильно установлен ноль стрелочного электроизмерительного прибора, погрешность от постоянного дополнительного веса на чашке весов и т.д. Переменными называются погрешности, изменяющиеся в процессе измерения. Они делятся на монотонно изменяющиеся, периодические и изменяющиеся по сложному закону. Если в процессе измерения систематическая погрешность монотонно возрастает или убывает, ее называют монотонно изменяющейся. Например, она имеет место при постепенном разряде батареи, питающей средство измерений. Периодической, называется погрешность, значение которой является периодической функцией времени. Примером может служить погрешность, обусловленная суточными колебаниями напряжения силовой питающей сети, температуры окружающей среды и др. Систематические погрешности могут изменяться и по более сложному закону, обусловленному какими-либо внешними причинами. По причинам возникновения погрешности делятся на методические, инструментальные и личные (субъективные). Эти погрешности подробно рассмотрены в разд. 4.1. 5.2. Способы обнаружения и устранениясистематических погрешностейРезультаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей. Это может быть достигнуто следующими путями: • устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений; • определением поправок и внесением их в результат измерения; • оценкой границ неисключенных систематических погрешностей. Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Действительно, результат одного измерения 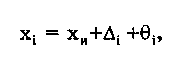 где хи — истинное значение измеряемой величины; i — i-я случайная погрешность; i — i-я систематическая погрешность. После усреднения результатов многократных измерений получаем среднее арифметическое значение измеряемой величины 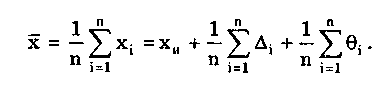 Если систематическая погрешность постоянна во всех измерениях, т.е. i = , то 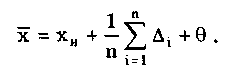 Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях. Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже. Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений. Для устранения постоянных систематических погрешностей применяют следующие методы: • Метод замещения, представляющий собой разновидность метода сравнения, когда сравнение осуществляется заменой измеряемой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не происходит никаких изменений. Этот метод дает наиболее полное решение задачи. Для его реализации необходимо иметь регулируемую меру, величина которой однородна измеряемой. Например, взвешивание по методу Борда [3], измерение сопротивления посредством моста постоянного тока и мер сопротивления [51]. • Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений. Например, способ взвешивания Гаусса [3]. Пример 5.1. Измерить сопротивление с помощью одинарного моста методом противопоставления. Сначала измеряемое сопротивление Rx уравновешивают известным сопротивлением R1, включенным в плечо сравнения моста. При этом Rx = R1R3/R4, где R3, R4 — сопротивления плеч моста. Затем резисторы Rx и R1 меняют местами и вновь уравновешивают мост, регулируя сопротивление резистора R1. В этом случае Rx = R1R3/R4. Из двух последних уравнений исключается отношение R3/R4. Тогда Rx = /R7RT • Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками. Пример 5.2. Измерить ЭДС потенциометром постоянного тока, имеющим паразитную термоЭДС. При выполнении одного измерения получаем ЭДС E1. Затем меняем полярность измеряемой ЭДС и направление тока в потенциометре. Вновь проводим его уравновешивание — получаем значение Е2. Если термоЭДС дает погрешность Е и Е1 =ЕХ + Е, то Е2 = ЕХ - Е. Отсюда Ех= (Е1 + Е2)/2. Следовательно, систематическая погрешность, обусловленная действием термоЭДС, устранена. • Метод рандомизации — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются. Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы. • Анализ знаков неисправленных случайных погрешностей. Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков "+" у случайных погрешностей сменяется последовательностью знаков "—" или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков "+" и "-" у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность. • Графический метод. Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей. • Метод симметричных наблюдений. Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y0, где х, у — входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у0 — постоянная. Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени t. При первом и третьем измерениях на вход преобразователя подается сигнал х0 от образцовой меры. В результате измерений получается система уравнений: 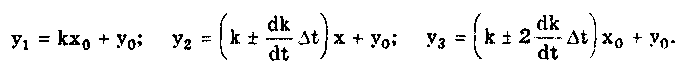 Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k: 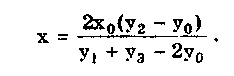 • Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и др. Исключение систематических погрешностей путем введения поправок. В ряде случаев систематические погрешности могут быть вычислены и исключены из результата измерения. Для этого используются поправки. Контрольные вопросы 1. Что такое систематическая погрешность? Приведите примеры. 2. Дайте определение исправленного результата измерений. 3. Каким образом классифицируются систематические погрешности? 4. Назовите способы выявления постоянных систематических погрешностей. 5. Назовите способы выявления переменных систематических погрешностей. 6. В чем состоит суть критерия Аббе? 7. Что такое дисперсионный анализ и как он применяется для устранения систематических погрешностей? 8. Как обнаружить систематическую погрешность при помощи критерия Вилкоксона? 9. Каким образом оценивается целесообразность введения поправки для устранения систематической погрешности? Глава 6. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ6.1. Вероятностное описание случайныхпогрешностейПрисутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения. Как уже отмечалось ранее, и результат измерения, и его погрешность с известными оговорками могут рассматриваться (см. разд. 4.2) как случайные величины. Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения. Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина хi в i-м опыте принимает значение, меньшее х: График интегральной функции распределения показан на рис. 6.1. Она имеет следующие свойства: • неотрицательная, т.е. F(x) 0; • неубывающая, т.е. F(x2) F(x1), если х2 x1; • диапазон ее изменения простирается от 0 до 1, т.е. F(- ) = 0; F(+ ) =1; • вероятность нахождения случайной величины х в диапазоне от х1 до х2 Р(x1 < х < х2} = F(x2) - F(x1). Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей р(х) = dF(x)/dx. Она всегда неотрицательна и подчиняется условию нормирования в виде: 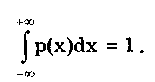 Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2) 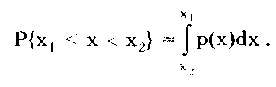 Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [- ; + ] равна единице, т.е. представляет собой достоверное событие. Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (х1;х2) равна площади, заключенной под кривой р(х) между абсциссами х1 и х2 (см. рис. 6.1). Поэтому по форме кривой плотности вероятности р(х) можно судить о том, какие значения случайной величины х наиболее вероятны, а какие наименее. 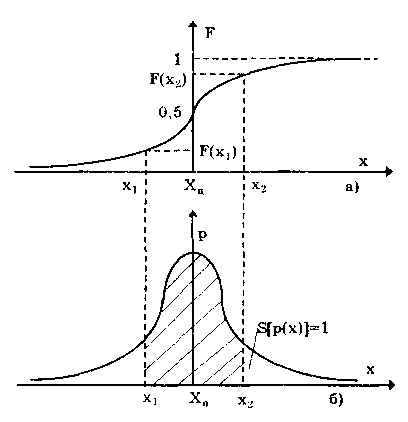 Рис. 6.1. Интегральная (а) и дифференциальная (б) функции распределения случайной величины Результирующая погрешность зачастую складывается из ряда составляющих с различными плотностями распределения р1(х), р2(х),..., рn(х). В связи с этим возникает задача определения суммарного закона распределения погрешности. Для суммы независимых непрерывных случайных х1 и х2, имеющих распределения р1(х) и р2(х), он называется композицией и выражается интегралами свертки [48, 49]:  Графическое определение композиции двух случайных независимых величин показано на рис. 6.2. Следует отметить, что масштаб всех графиков по вертикали произвольный, и должно выполняться условие: площадь, ограниченная кривой плотности вероятности, равна единице. 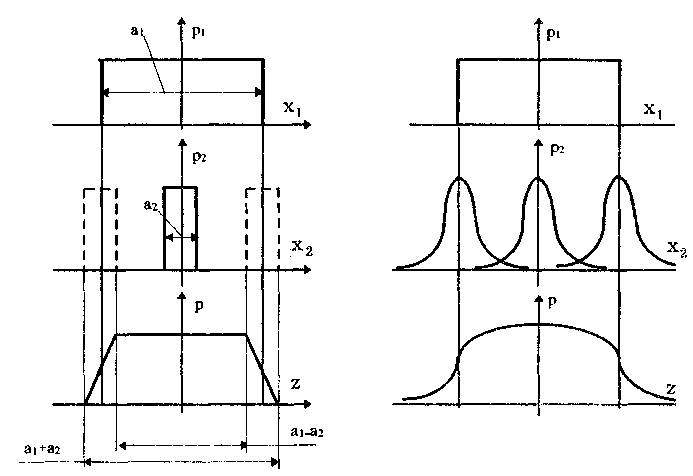 Рис. 6.2. Суммирование законов распределений 6.3. Основные законы распределения6.3.1. Общие сведенияИспользование на практике вероятностного подхода к оценке погрешностей результатов измерений прежде всего предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. В качестве примера можно привести результаты исследований [4] 219 фактических распределений погрешностей, имеющих место при измерении электрических и неэлектрических величин разнообразными приборами. Установлено, что примерно 50% распределений принадлежат к классу экспоненциальных, 30% являются уплощенными, а остальные 20% — различными видами двухмодальных распределений. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать [4] следующим образом: • трапецеидальные (плосковершинные) распределения; • уплощеные (приблизительно плосковершинные) распределения; • экспоненциальные распределения; • семейство распределений Стьюдента; • двухмодальные распределения. 6.3.2. Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерноe распределение (рис. 6.5,а) описывается уравнением 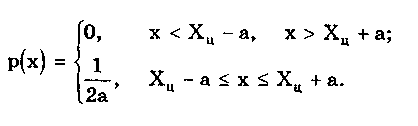 Трапецеидальное распределение (рис. 6.5, б) образуется как композиция двух равномерных распределений шириной а1 и а2, (рис. 6.2): 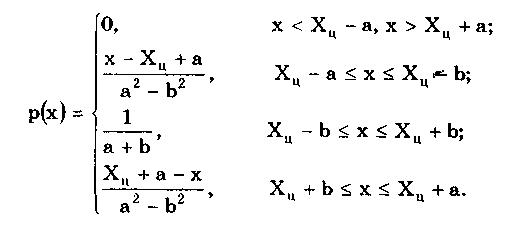 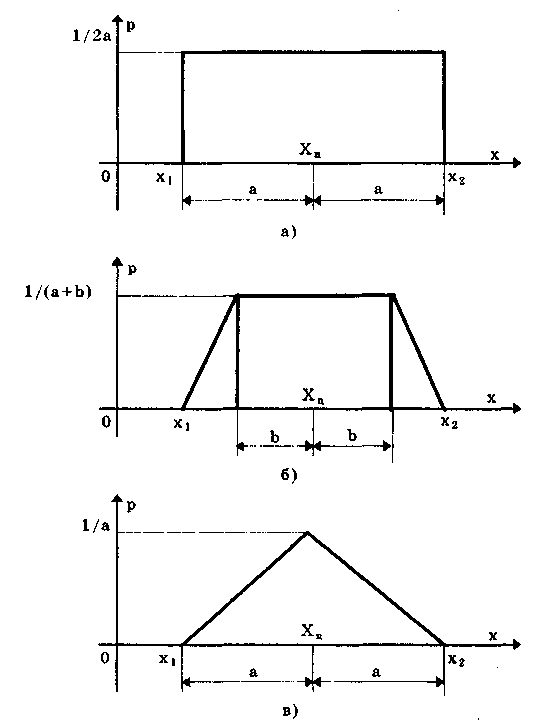 Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона) Треугольное (Симпсона) распределение (рис. 6.5, в) — это частный случай трапецеидального, для которого размеры исходных равномерных распределений одинаковы: а1 = а2 (см. рис. 6.2):  где Хц, а, b — параметры распределения. Математическое ожидание всех трапецеидальных распределений Хц = (x1 + х2) / 2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а. Среднее квадратическое отклонение в зависимости от распределения определяется по формуле: • равномерное • трапецеидальное • треугольное Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл. 6.2. Таблица 6.2 Значения параметров трапецеидальных распределений
Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон. 6.3.3. Экспоненциальные распределенияЭкспоненциальные распределения описываются формулой [4] 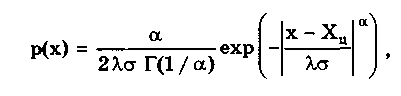 (6.5) (6.5)где 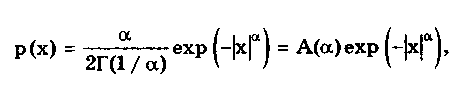 где А(а) — нормирующий множитель распределения. Интегральная функция нормированного экспоненциального распределения описывается выражением 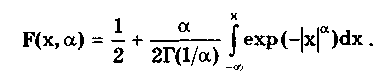 Интеграл, входящий в эту формулу, выражается через элементарные функции только при = 1/n, n = 1; 2; 3; ... При = n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам, приведенным в [53]. Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам: 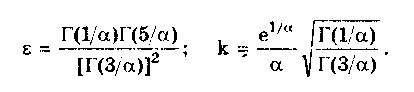 Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При < 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При = 1 получается распределение Лапласа р(х) = 0,5е-|x| , при = 2 — нормальное распределение или распределение Гаусса. При > 2 распределения, описываемые формулой (6.5), близки по свойствам к трапецеидальным. При очень больших значениях формула (6.5) описывает практически равномерное распределение. В табл. 6.3 приведены параметры некоторых из экспоненциальных распределений. Таблица 6.3 Значения параметров экспоненциальных распределений при различных показателях a
6.3.4. Нормальное распределение (распределениеГаусса)Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса: 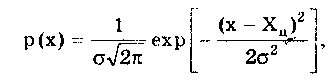 (6.6) (6.6)где — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО. Вид нормального распределения показан на рис. 6.3. 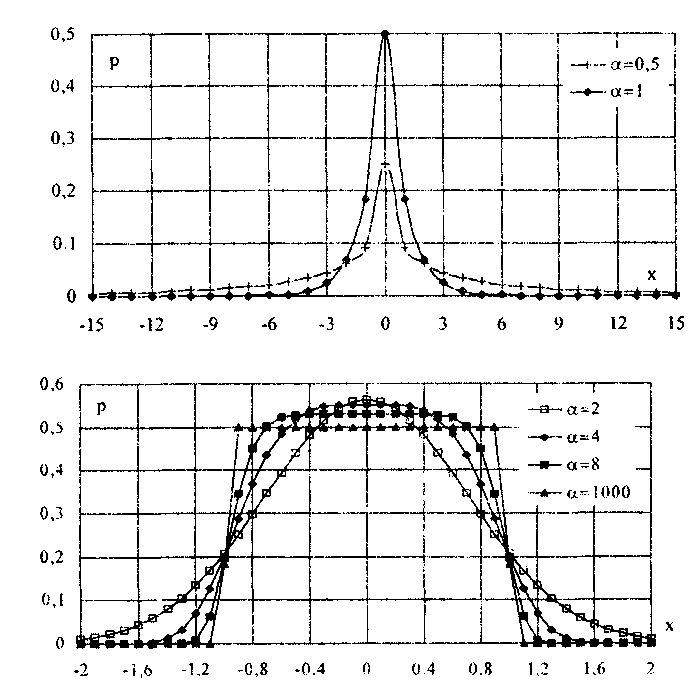 Рис. 6.6. Экспоненциальные распределения, определяемые по формуле (6.5) при = 1 и Хц = 0 Широкое использование нормального распределения на практике объясняется центральной предельной теоремой теории вероятностей [48, 49], утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. 6.3.6. Семейство распределений СтъюдентаЭти законы описывают плотность распределения вероятности среднего арифметического, вычисленного по выборке из n случайных отсчетов нормально распределенной генеральной совокупности. Распределения Стьюдента нашли широкое применение при статистической обработке результатов многократных измерений. Их вид зависит от числа отсчетов n, по которым находится среднее арифметическое значение. Контрольные вопросы. 1. При каких условиях погрешность измерения может рассматриваться как случайная величина? 2. Перечислите свойства интегральной и дифференциальной функций распределения случайной величины. 3. Назовите числовые параметры законов распределения. 4. Каким образом может задаваться центр распределения? 5. Что такое моменты распределения? Какие из них нашли применение в метрологии? 6. Назовите основные классы распределений, используемых в метрологии. 7. Дайте характеристику распределениям, входящим в класс трапецеидальных распределений. 8. Что такое экспоненциальные распределения? Каковы их свойства и характеристики? 9. Что такое нормальное распределение? Почему оно играет особую роль в метрологии? 10. Что такое функция Лапласа и для чего она используется? 11. Как описывается и где используется семейство распределений Стьюдента? 12. Какие точечные оценки законов распределения вы знаете? Какие требования предъявляются к ним? 13. Что такое доверительный интервал? Какие "способы его задания вам известны? |
