Метрология. Лекц Метрология. Предмет и задачи метрологии

• Название: Предмет и задачи метрологии
• Анкор: Метрология
• Дата: 03.12.2021
• Размер: 1.64 Mb.
• Имя файла: Лекц Метрология.doc
• Тип: Глава; #290110
• страница: 6 из 20

Глава 9. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ

9.1. Основы теории суммирования погрешностей

Определение расчетным путем оценки результирующей погрешности по известным оценкам ее составляющих называется суммированием погрешностей.

Главной проблемой, возникающей при суммировании, является то, что все составляющие погрешности должны рассматриваться как случайные величины. С точки зрения теории вероятностей они наиболее полно могут быть описаны своими законами распределения, а их совместное действие — соответствующим многомерным распределением. Однако в такой постановке задача суммирования погрешностей практически не разрешима уже для нескольких составляющих, не говоря о нескольких десятках.

Практически приемлемый путь решения данной задачи суммирования погрешностей состоит в отказе от определения и использования многомерных функций распределения составляющих погрешности. Необходимо подобрать для характеристик составляющих такие числовые оценки (СКО, эксцесс и др.), оперируя с которыми можно было бы получить соответствующие числовые оценки результирующей погрешности. При этом следует учитывать, что:

• отдельные составляющие погрешности могут быть коррелиро-ваны между собой;

• при суммировании случайных величин их законы распределения существенно деформируются, т.е. форма закона суммы может резко отличаться от формы закона распределения составляющих.

Правила суммирования погрешностей основываются [4] на том, что погрешность по абсолютному значению всегда много меньше самой измеряемой величины. Поэтому изменение погрешности в зависимости от изменения измеряемой величины может быть учтено, если все суммируемые случайные и систематические составляющие погрешности разделить на аддитивные и мультипликативные. Сумма аддитивных составляющих даст значение аддитивной части результирующей погрешности, а сумма мультипликативных составляющих — значение мультипликативной части результирующей погрешности.

В пределах некоторого диапазона изменения, как правило, десятикратного, измеряемой величины изменение результирующей погрешности может быть с достаточной степенью точности представлено прямой линией или простейшей кривой (парабола, гипербола). Это дает возможность описать результирующую погрешность линейной или нелинейной двузвенной формулой. При большем изменении измеряемой величины весь диапазон разбивается на участки, для которых и определяются крайние погрешности.

9.2. Суммирование систематических

погрешностей

При определении границ систематическая погрешность оценивается по ее составляющим, называемым элементарными систематическими погрешностями. Если для части составляющих находят их оценки и эти погрешности устраняют введением поправок, то в качестве рассматриваемых элементарных погрешностей выступают погрешности определения поправок, которые также характеризуются границами.

При большом числе слагаемых результирующая погрешность имеет практически нормальное распределение. Оценка дисперсии этого распределения равна сумме дисперсий слагаемых:

9.3. Суммирование случайных погрешностей

Правила суммирования случайных погрешностей основаны на известных из теории вероятностей положениях:

а) оценка математического ожидания результирующей погрешности определяется алгебраической суммой оценок математических ожиданий составляющих;

б) оценка СКО суммарной погрешности определяется выражением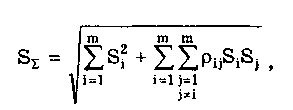

(9.7)

где S_i — оценка СКО i-й составляющей погрешности; m — число суммируемых составляющих погрешностей; ρ_ij — коэффициент корреляции между i- и j-й составляющими.

9.4. Суммирование систематических и

случайных погрешностей

При проведении многократных измерений случайная погрешность может быть уменьшена во много раз. Однако погрешность усредненного результата будет определяться не этой весьма малой случайной погрешностью, а не зависящей от числа усредняющих отсчетов систематической погрешностью.

Механизм суммирования систематической и случайной составляющих погрешности отличается от механизма суммирования случайных погрешностей. Согласно ГОСТ 8.207—76 погрешность результата измерения определяется по следующим правилам. Если границы неисключенной систематической погрешности 6 и оценка СКО результата измерения S связаны соотношением

(9.16)

то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата. При этом доверительные границы погрешности результата  = t_pS, где t_p — коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа проведенных измерений п. Если же имеет место неравенство

(9.17)

то, наоборот, следует пренебречь случайной составляющей и результат характеризовать лишь границами его суммарной систематической погрешности  = . Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности, при выполнении указанных неравенств не превышает 15%.