нормальный закон распределения случайных величин. Нормальный закон распределения случайных величин
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
РОССИЙСКИЙ университет ТРАНСПОРТА (МИИТ) _____________________________________________________________________________ Кафедра «Здания и сооружения на транспорте» Доклад на тему: Нормальный закон распределения случайных величин Выполнил студент – Мороз Е.В., группа СГС-311 Научный руководитель – к.т.н., доцент Терехов И.А. Москва 2020 Нормальный закон распределения случайных величин Нормальный закон распределения называют еще законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения. Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надежности его используют для описания постепенных отказов, когда распределение времени безотказной работы вначале имеет низкую плотность, затем максимальную и далее плотность снижается. Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы. Нормальный закон распределения описывается плотностью вероятности 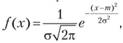 где е = 2,71828 – основание натурального логарифма; π = 3,14; т и σ – параметры распределения, определяемые по результатам испытаний. Колоколообразная кривая плотности распределения 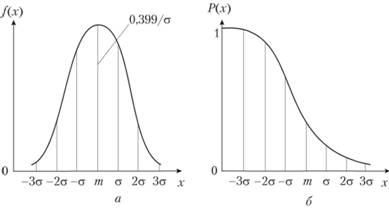 Кривые плотности вероятности (а) и функции надежности (б) для нормального распределения Параметр т = Мх представляет собой (в пределе, по теореме Гливенко) среднее значение случайной величины х, оцениваемое по формуле Параметр σ – среднее квадратическое отклонение случайной величины х, оцениваемое по формуле 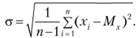 Интегральная функция распределения имеет вид 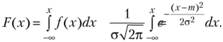 Вероятность отказа Q(x) = F(x), вероятность безотказной работы R(x) = 1 – F(x). Вычисление интегралов заменяют использованием таблиц нормального распределения, в которых Мх = 0 и σ = 1. Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью  Величина t является центрированной (так как Мt = 0) и нормированной (так как σt = 1). Функцию распределения соответственно можно записать в виде 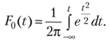 Из уравнения следует, что F0(t) + F0(-t) = 1, или F0(-t) = 1-F0(t). В формулу вместо t следует подставить значение 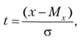 при этом t называют квантилем нормированного нормального распределения (в литературе часто обозначают ир). Плотность распределения и вероятность отказа соответственно равны f(x) = f0(t)/σ и Q(x) = F0(t). Тогда вероятность безотказной работы R(x) = 1 – f0(t), где f0(t) и F0(t) определяют по таблице Оуэн Д. Б. Сборник статистических таблиц. В работах по надежности часто вместо интегральной функции распределения F0(t) используют функцию Лапласа 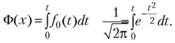 Очевидно, что  Вероятности отказа и безотказной работы, выраженные через функцию Лапласа: 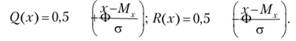 Вероятность попадания случайной величины X в заданный интервал значений от а до β вычисляют по формуле 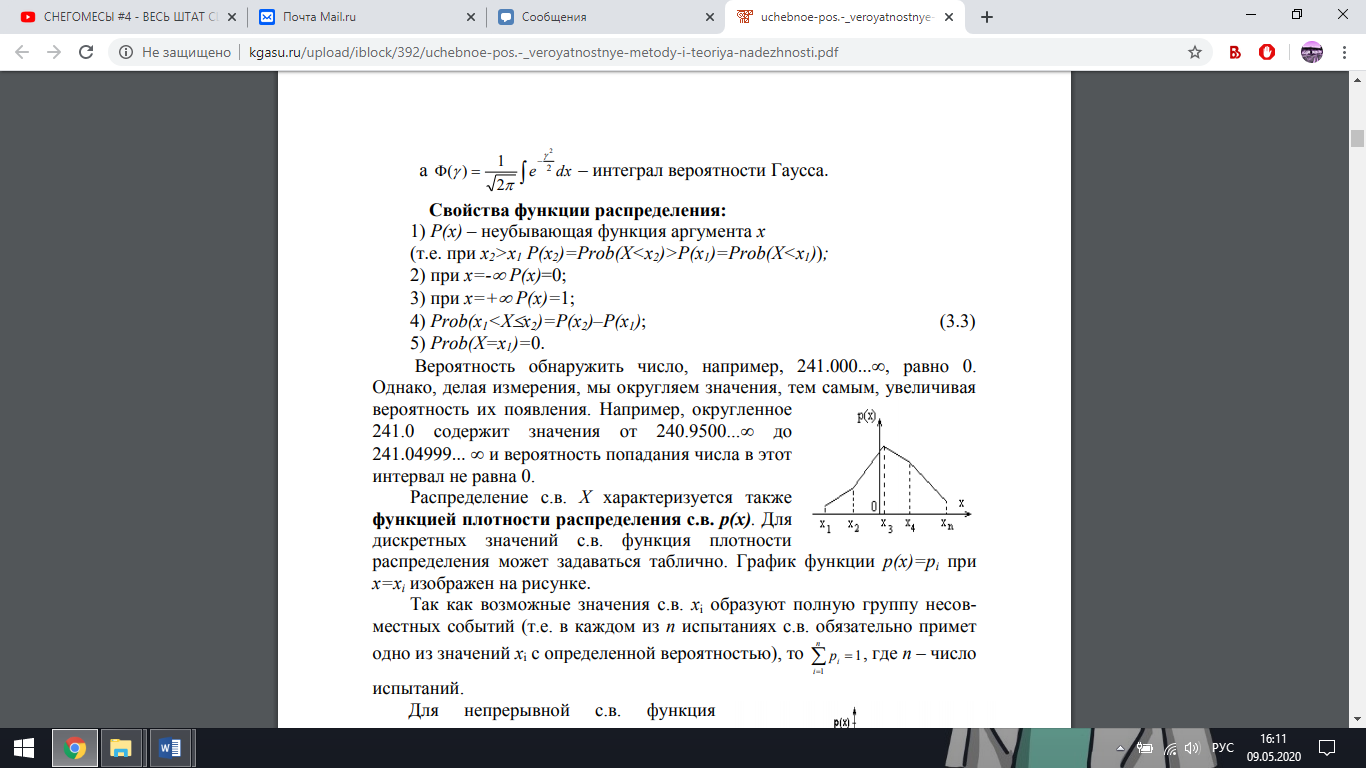  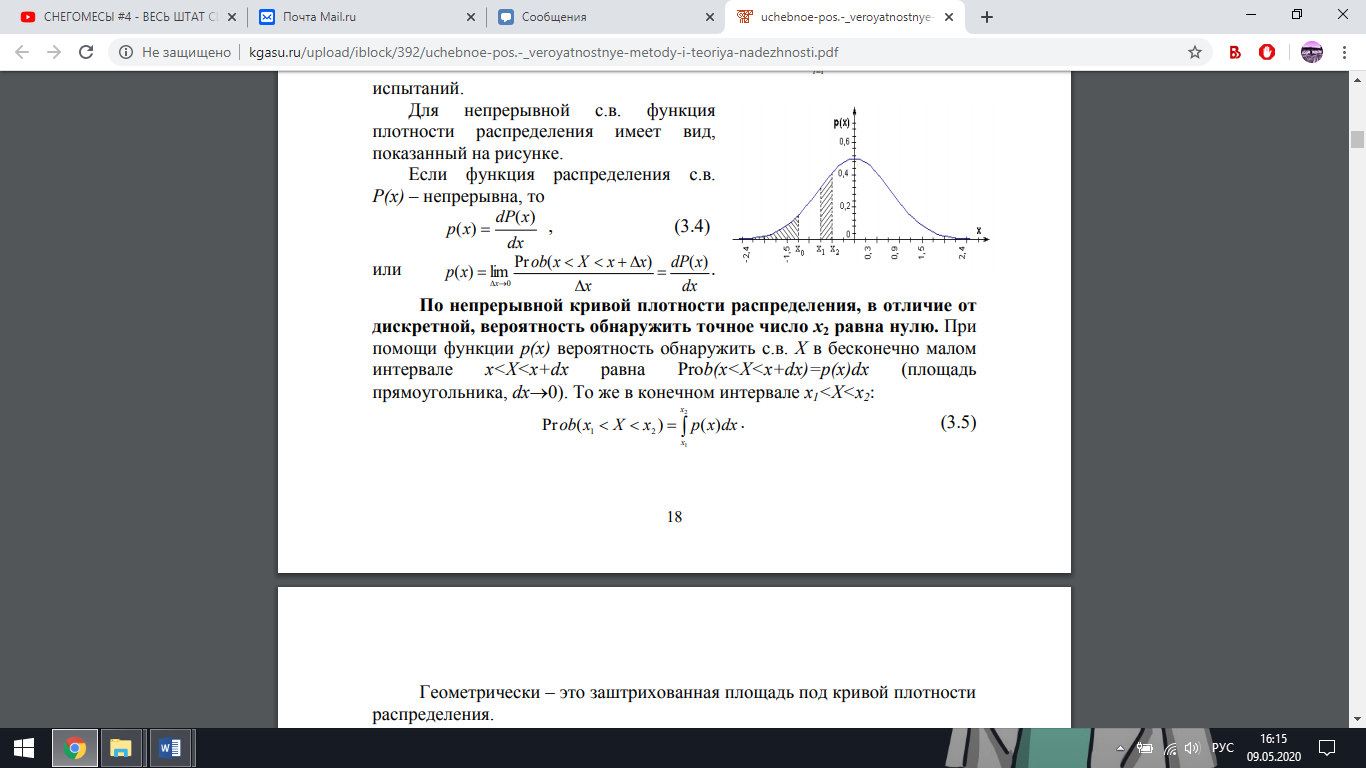   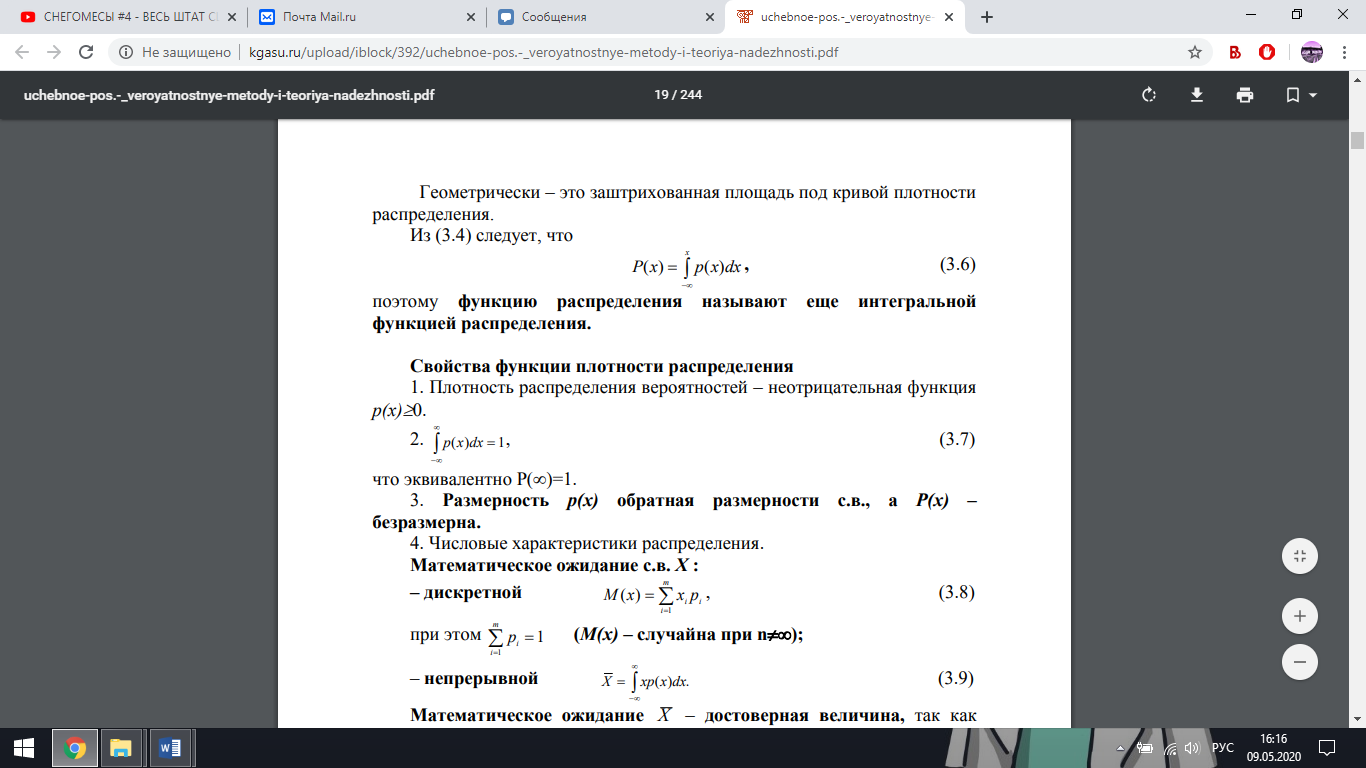       Список литературы: В.И. Лукашенко «ВЕРОЯТНОСТНЫЕ МЕТОДЫ СТРОИТЕЛЬНОЙ МЕХАНИКИ И ТЕОРИЯ НАДЕЖНОСТИ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ».     |
