Анализ использования показательного
 Скачать 49.18 Kb. Скачать 49.18 Kb.
|
|
УДК 62 -192 + 519.248 АНАЛИЗ ИСПОЛЬЗОВАНИЯ ПОКАЗАТЕЛЬНОГО ТЕХНИЧЕСКИХ СИСТЕМ Р. С. Литвиненко, Р. Г. Идиятуллин, А. Э. Аухадеев ' Введение Для описания отказов системы могут быть предложены модели, предназначенные для решения различных задач надежности и по-разному учитывающие комплекс факторов, присущих характеру отказов. Случайный характер возникновения отказов в процессе эксплуатации технических систем и их элементов позволяет применять в их описании вероятностно-статистические методы. Наиболее распространенными являются модели отказов, основанные на распределении соответствующих случайных величин - наработок до отказа невосстанавливаемых объектов и наработок между отказами восстанавливаемых объектов. В качестве основных видов распределения наработок изделий до отказа следует выделить [1]: экспоненциальное; Вейбулла - Гнеденко; гамма; логарифмически нормальное; нормальное. В результате обзора отечественной и зарубежной литературы дана оценка практического применения экспоненциального закона распределения в области надежности технических систем. Статистические характеристики показательного (экспоненциального) распределения Экспоненциальное распределение хотя и является частным случаем распределения Вейбулла - Гнеденко (при а = 1), но представляет большой самостоятельный интерес, так как оно адекватно описывает распределение длительности работы элемента в период нормальной эксплуатации. Прикладная популярность экспоненциального закона объясняется не только разнообразными возможностями его естественной физической интерпретации, но и исключительной простотой и удобством его модельных свойств. Ниже представлены формулы для определения плотности и вероятности безотказной работы в течение времени t, соответствующей этому закону: f (t) = Xe-Xt; P(t) = e-X, где X = = - параметр распределения (интенсивность отказов); t - математическое ожидание случайной величины. График плотности распределения показательного (экспоненциального) распределения представлен на рис. 1. Математическое ожидание m и среднее квадратическое отклонение а для показательного распределения выражаются через его параметр Отсюда видно, что для случайных величин, распределенных по экспоненциальному закону, коэффициент вариации v равен единице, так как о = m . 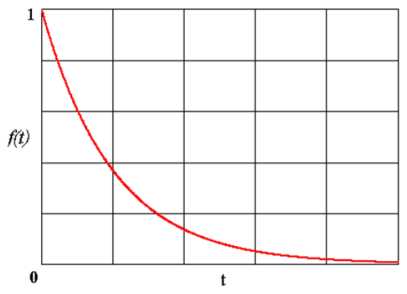 Рис. 1. График плотности экспоненциального распределения Также для экспоненциального распределения могут быть представлены следующие числовые характеристики: мода Mo = 0; медиана Me = ln2 / A = 0,6931/ A = 0,6931 • m ; дисперсия D = 1/ A2 ; коэффициент ассиметрии As = 2; эксцесс Ex = 9 . Средняя наработка до первого отказа равна На рис. 2 изображены кривые вероятностей безотказной работы P(t) и отказа Q(t), а также графическое представление средней наработки до первого отказа при показательном (экспоненциальном) распределении. 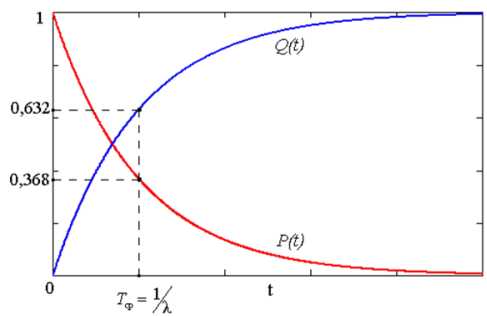 Рис. 2. Вероятность безотказной работы P(t) и вероятность отказа Q(t) при экспоненциальном распределении Статистические свойства показательного (экспоненциального) распределения Экспоненциальное (показательное) распределение часто используют на стадии разработки, когда информация о надежности элементов создаваемой системы ограничена либо полностью отсутствует, поэтому его часто называют основным законом надежности [2]. Ограничением для применения этого закона является необходимость, чтобы потоки отказов и восстановлений были простейшими (обладали свойствами ординарности, стационарности и отсутствия последействия) [3, 21]. Согласно [4-14] экспоненциальное распределение хорошо описывает надежность техники, эксплуатируемой после окончания приработки и до существенного проявления постепенных отказов, т.е. в период нормальной эксплуатации, когда преобладают внезапные отказы. В [2, 7] сказано, что время безотказной работы технических систем с большим числом последовательно соединенных элементов может быть описано этим распределением, если каждый из элементов в отдельности не оказывает большого влияния на отказ системы. В этом случае, если отказы последовательно соединенных элементов будут иметь экспоненциальное распределение, то и отказы самой системы будут подчинены этому же закону, а ее интенсивность отказов будет равна сумме интенсивностей отказов элементов. Необходимо обратить внимание на то обстоятельство, что системы, содержащие непоследовательно соединенные в смысле надежности элементы, уже не будут обладать экспоненциальным распределением, несмотря на экспоненциальность вероятностей безотказной работы входящих в ее состав элементов [3]. Поскольку каждый элемент системы в свою очередь сам является подсистемой, состоящей из нескольких, а часто и большого числа элементов, суммарная интенсивность отказов элементов системы зависит только от числа неисправных элементов, а время ремонта каждого отказавшего элемента имеет показательное распределение. Отказ такой подсистемы есть отказ одного из ее элементов, который при восстановлении заменяется новым. Чистое время работы подсистемы определяет, что ее поток отказов будет суммой большого числа потоков, и согласно предельной теореме Хин- чина он асимптотически будет пуассоновским потоком. Отсюда можно сделать вывод, что интервал времени между соседними отказами будет иметь показательное распределение [15, 16]. Экспоненциальный закон следует применять для тех сложных технических систем, в которых может одновременно происходить много различных разрушающих процессов, протекающих с различными скоростями. Однако по мере уменьшения разнородности скоростей процессов распределение приближается к нормальному, а при преобладании однотипных процессов разрушения - в точности соответствует нормальному [11]. Авторы работ [2, 4, 6, 17] считают, что при решении проблем, связанных с обслуживанием сложных систем, если поток восстановления является простейшим, экспоненциальный закон применяется при описании интенсивности восстановления, трудоемкости текущего ремонта и устранения отказов. В задачах массового обслуживания интервалы между моментами поступления техники в ремонт также хорошо описываются экспоненциальным законом [3]. Поскольку в период нормальной эксплуатации внезапный отказ возникает лишь как следствие внешних воздействий, то замена старого элемента на новый не может повлиять на причину отказа. По этой причине при экспоненциальном законе распределения времени безотказной работы нет смысла прибегать к профилактическим мерам, например, предварительной замене элементов или их периодическому ремонту [18]. Есть мнение [2, 3, 19], что если рассматривать физическую сущность внезапных отказов, то показательным законом можно аппроксимировать вероятности безотказной работы большого числа технических объектов, в первую очередь элементов радиоэлектронной аппаратуры, электрических и электронных аппаратов, аппаратно-программных комплексов и др. Ограничения использования показательного (экспоненциального) распределения Однако, несмотря на всю простоту и универсальность, экспоненциальный закон обладает рядом ограничений. Данному распределению характерно свойство «отсутствия памяти», обладающее большим недостатком, а именно: противоречием естественным физическим представлениям. Это свойство означает отсутствие старения, т.е. технический объект не стареет или, проработав какое-то время, будет иметь одинаковое с новым объектом распределение отказов, что неправомерно при эксплуатации многих технических объектов, особенно на больших временных интервалах [3, 13]. По-видимому, экспоненциальное распределение будет несправедливым и для времени восстановления, так как продолжительность ремонта ограничена и выражается дробным или целым числом, поэтому время, которое осталось затратить на окончание восстановления, будет зависеть от уже затраченного времени восстановления [20]. В [3] не без оснований утверждается, что экспоненциальный закон распределения к сложным техническим системам не применим, так как неодновременность работы элементов и наличие последействия отказов обусловливают, что интенсивность отказов сложной системы не может быть постоянной, даже при условии постоянства интенсивностей отказов ее элементов. Следовательно, использование этого закона для анализа надежности реальных технических систем длительного функционирования - неправомерно, а исходные предпосылки в моделях не адекватны физическим процессам, протекающим в системах. Заключение Все это говорит о том, что надо иметь достаточные основания для применения экспоненциального распределения, как и для любого другого. Тем не менее это распределение является одним из распространенных, что объясняется следующими причинами: простотой и зависимостью только от одного параметра X . Это обстоятельство вместе со свойством отсутствия последействия позволяет решать многие задачи теории надежности и представлять решение в явном аналитическом виде; доказано, что время безотказной работы сложных высоконадежных восстанавливаемых систем при определенных условиях (например, возможность пренебречь влиянием «старения» материалов) хорошо описывается показательным распределением; применение экспоненциального закона в тех случаях, когда оно несправедливо, позволяет при определенных условиях получать заниженные результаты показателей надежности, т.е. оценки снизу, что зачастую является приемлемым. Список литературы ГОСТ Р 27.001-2009. Надежность в технике. Модели отказов. - М. : Стандартинформ, 2010. - 16 с. Труханов, В. М. Надежность технических систем типа подвижных установок на этапе проектирования и испытания опытных образцов / В. М. Труханов. - М. : Машиностроение, 2003. - 320 с. Половко, А. М. Основы теории надежности : учеб. пособие / А. М. Половко, С. В. Гуров. - 2-е изд., пе- рераб. и доп. - СПб. : БХВ-Петербург, 2006. - 704 с. Лисунов, Е. А. Практикум по надежности технических систем : учеб. пособие / Е. А. Лисунов. - 2-е изд., перераб. и доп. - СПб. : Лань, 2015. - 240 с. Павлов, И. В. Статистические методы оценки надежности сложных систем по результатам испытаний / И. В. Павлов. - М. : Радио и связь, 1982. - 168 с. Электроподвижной состав. Эксплуатация, надежность и ремонт : учеб. / под ред. А. Т. Головатого, П. И. Борцова. - М. : Транспорт, 1983. - 350 с. Хазов, Б. Ф. Справочник по расчету надежности машин на стадии проектирования / Б. Ф. Хазов, Б. А. Дидусев. - М. : Машиностроение, 1986. - 224 с. Гнеденко, Б. В. Математические методы в теории надежности. Основные характеристики надежности и их статистический анализ / Б. В. Гнеденко, Ю. К. Беляев, А. Д. Соловьев. - М. : Либроком, 2013. - 584 с. Гнеденко, Б. В. Вопросы математической теории надежности / Б. В. Гнеденко. - М. : Радио и связь,1983. - 376 с. Машиностроение : энцикл. : в 40 т. Т. IV-3: Надежность машин / В. В. Клюев, В. В. Болотин, Ф. Р. Соснин [и др.] ; под общ. ред. В. В. Клюева. - М. : Машиностроение, 2003. - 592 с. Комаров, А. А. Надежность гидравлических систем / А. А. Комаров. - М. : Машиностроение, 1969. - 236 с. Венников, Г. В. Надежность и проектирование / Г. В. Венников. - М. : Знание, 1971. - 96 с. Жаднов, В. В. Анализ моделей прогнозирования и расчета надежности комплектующих элементов бортовой электронной аппаратуры / В. В. Жаднов // Труды международного симпозиума Надежность и качество. - 2013. - Т. 1. - С. 28-31. Каштанов, В. А. Стратегия технического обслуживания на основе полумарковских процессов с конечным множеством состояний / В. А. Каштанов // Надежность и качество сложных систем. - 2013. - № 1. - С. 41-46. Надежность в технике : справ. : в 10 т. Т. 2: Математические методы в теории надежности и эффективности / под ред. Б. В. Гнеденко. - М. : Машиностроение, 1987. - 280 с. Айвазян, С. А. Прикладная статистика и основы эконометрики : учеб. для вузов / С. А. Айвазян, В. С. Мхитарян. - М. : ЮНИТИ, 1998. - 1022 с. Надежность технических систем : справ. / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин [и др] ; под ред. И. А. Ушакова. - М. : Радио и связь, 1985. - 608 с. Герцбах, И. Б. Модели отказов / И. Б. Герцбах , Х. Б. Кордонский ; под ред. Б. В. Гнеденко. - М. : Советское радио, 1966. - 166 с. Юрков, Н. К. Системный подход к организации жизненного цикласложных технических систем / Н. К. Юрков // Надежность и качество сложных систем. - 2013. - № 1. - С. 27-34. Каштанов, В. Н. Теория надежности сложных систем : учеб. пособие / В. Н. Каштанов, А. И. Медведев. - М. : ФИЗМАТЛИТ, 2010. - 609 с. Анализ статистики отказов выключателей 110 кВ Пензенской энергосистемы / Н. Н. Денисова, Ю. А. Шатова, В. Я. Горячев, К. Я. Умяров // Труды международного симпозиума Надежность и качество. - 2015. - Т. 2. - С. 97-100. Литвиненко Руслан Сергеевич кандидат технических наук, доцент, кафедра электротехнических комплексов и систем, Казанский государственный энергетический университет (420066, Россия, г. Казань, ул. Красносельская, 51) E-mail: litrus@km.ru ИДиятуллин Ринат Гаисович доктор технических наук, профессор, кафедра электротехнических комплексов и систем, Казанский государственный энергетический университет (420066, Россия, г. Казань, ул. Красносельская, 51) E-mail: litrus277@yandex.ru АухаДеев Авер Эрикович кандидат технических наук, доцент, кафедра электротехнических комплексов и систем, Казанский государственный энергетический университет (420066, Россия, г. Казань, ул. Красносельская, 51) E-mail: auhadeevkgma@rambler.ru Аннотация. Актуальность и цели. В практике эксплуатации технических систем в большинстве случаев приходится иметь дело с вероятностными (случайными) процессами, когда функция отражает аргумент с некоторой вероятностью. Наиболее полно случайная величина описывается законом распределения вероятностей, основным из которых в теории надежности технических систем является экспоненциальное (показательное) распределение. В условиях неопределенности информации о законе распределения времени наступления отказов вследствие малых объемов статистических данных, что как правило бывает на начальных этапах разработки техники, исследователю приходится принимать решение о выборе априорной модели надежности, исходя из опыта предыдущей эксплуатации прототипов или аналогов. Систематизация информации о практическом использовании показательного распределения при прогнозировании и оценке надежности различных технических систем является актуальной научной задачей. Материалы и методы. В основе изложенного материала лежит систематизация информации, опубликованной в отечественной и зарубежной литературе и представляющей анализ результатов модельных и экспериментальных исследований надежности техники, а также статистические данные, полученные в ходе эксплуатации. Результаты. Представленная теоретическая информация о применении показательного закона в теории надежности может быть использована в качестве первого приближения и подлежит обязательному уточнению с использованием различных критериев проверки гипотез по мере увеличения объема статистических данных в ходе последующих испытаний. Выводы. Надо иметь достаточно оснований для применения экспоненциального закона распре- Litvinenko Ruslan Sergeevich candidate of technical sciences, associate professor, sub-department of electrotechnical complexes and systems, Kazan State Power Engineering University (420066, 51 Krasnoselskaya street, Kazan, Russia) Idijatullin Rinat Gaisovich doctor of technical sciences, professor, sub-department of electrotechnical complexes and systems, Kazan State Power Engineering University (420066, 51 Krasnoselskaya street, Kazan, Russia) Auhadeev Aver Erikovich candidate of technical sciences, associate professor, sub-department of electrotechnical complexes and systems, Kazan State Power Engineering University (420066, 51 Krasnoselskaya street, Kazan, Russia) Abstract. Background. In practice, operation of technical systems in most cases have to deal with stochastic (random) processes, when the function reflects the argument with a certain probability. Most completely random variable described by a probability distribution, the basic one in the theory of reliability of technical systems is exponential (exponential) distribution. In the face of uncertainty about the law of distribution of time of occurrence of failures due to small amounts of statistical data, which usually happens in the initial stages of technology development, the researcher has to decide on the choice of prior model reliability based on previous operating experience of prototypes or analogues. Systematization of information on the practical use of exponential distribution in predicting and assessing the reliability of various technical systems is an important scientific task. Materials and methods. In the above material is the systematization of the information published in domestic and foreign literature, and representing the analysis results of model and experimental studies of reliability of equipment, as well as statistical data obtained during operation. Results. Presents theoretical information on the use of exponential law of reliability theory can be used as a first approximation and is subject to obligatory specification, using different criteria of testing hypotheses, increasing the volume of statistical data in subsequent tests. Conclusions. It is necessary to have sufficient grounds for application of exponential distribution law, like any other. Therefore, the article may be useful for researchers in the early stages of development or modernization of technical systems, as a priori information to build the models and criteria used to ensure and control the reliability. деления, как и любого другого. Поэтому статья может быть полезна исследователям на ранних этапах разработки или модернизации технической системы в качестве априорной информации для построения моделей и критериев, используемых для обеспечения и контроля надежности.  Key words: reliability, distribution, operation time, probability, density of distribution, stage, expected value. Ключевые слова: надежность, распределение, наработка, вероятность, плотность распределения, этап, математическое ожидание. УДК 62 -192 + 519.248 Литвиненко, Р. С. Анализ использования показательного распределения в теории надежности технических систем / Р. С. Литвиненко, Р. Г. Идиятуллин, А. Э. Аухадеев // Надежность и качество сложных систем. - 2016. - № 2 (14). - С. 17-22.  |
