Метрология. Лекц Метрология. Предмет и задачи метрологии

• Название: Предмет и задачи метрологии
• Анкор: Метрология
• Дата: 03.12.2021
• Размер: 1.64 Mb.
• Имя файла: Лекц Метрология.doc
• Тип: Глава; #290110
• страница: 13 из 20

11.7.2. Структурная схема прямого преобразования

Отличительная черта СИ, имеющего структурную схему прямого преобразования (рис. 11.22), состоит в том, что все преобразования Измерительного сигнала производятся в прямом направлении. Схема состоит из n последовательно соединенных блоков.



Рис. 11.22. Структурная схема прямого преобразования
На схеме через К₁, К.,, ..., К_n обозначены коэффициенты преобразования блоков. Каждый i-й коэффициент определяется по формуле К = dU_i/dU_i-1, где

U_i-1 и U_i — входной и выходной сигналы i-го блока.

Входной сигнал U_вх, несущий информацию об измеряемой величине, последовательно преобразуется в промежуточные сигналы U1, U₂,..., U_n-1 и в выходной сигнал U_выx. В общем случае каждый из них является переменным во времени и может быть представлен в виде суммы гармонических составляющих. В связи с этим коэффициент К_i должен выражаться комплексным числом, а анализ структурных схем проводиться с использованием теории функций комплексного переменного. Однако для простоты рассмотрения будем считать, что информативным параметром сигнала является только его амплитуда (это чаще всего и бывает на практике). Тогда коэффициенты преобразования выразятся вещественными числами. Предположим также, что коэффициенты преобразования не зависят от уровня сигнала, т.е. звенья считаются линейными: К₍ = const.

Первоначально считая, что все помехи AU_oi (см. рис. 11.22) равны нулю, получим уравнение преобразования СИ, имеющего структурную схему прямого преобразования: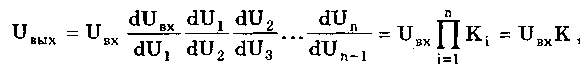

, (11.10)

где К — коэффициент преобразования СИ.

На процесс измерения будут оказывать влияние изменения и нестабильность коэффициентов преобразования К_i, а также дрейфы нуля, помехи и наводки, которые в сумме можно описать сигналами U_0i, складываемыми с выходными сигналами каждого блока. Абсолютная погрешность U_вых измерения выходной величины, обусловленная нестабильностью коэффициента преобразования, может быть рассчитана как погрешность косвенного измерения с учетом выражения (11.10):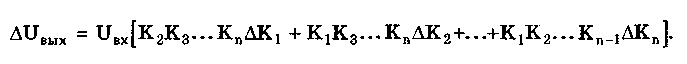



Как видно из этого уравнения, погрешность U_вых является мультипликативной, т.е. зависит от уровня измеряемого сигнала. Относительная мультипликативная погрешность складывается из относительных погрешностей структурных элементов: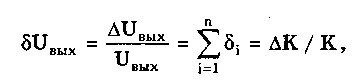



где _ш = К_i/К_i — относительная нестабильность коэффициента преобразования i-го блока; К/К - относительная нестабильность коэффициента преобразования СИ.

Рассмотрим погрешность, обусловленную дрейфом нуля и наводками. Дрейф нуля — это изменение сигнала на выходе блока, не связанное с изменением входного сигнала. Он, как правило, определяется при входном сигнале, равном нулю. Дрейф нуля приводит к смещению передаточной функции 1-го элемента (рис. 11.23,а). Результирующее действие сигналов U_0i приводит к появлению дополнительного выходного сигнала



Эта погрешность приведена к выходу СВ и по своей сути является аддитивной.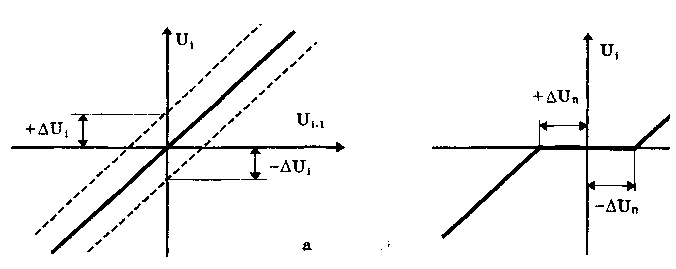


Рис. 11.23. Функции преобразования блоков с дрейфом нуля (а)

и порогом чувствительности (б)
Таким образом, как следует из двух последних уравнений, в СИ, имеющем структурную схему прямого преобразования, происходит суммирование погрешностей, вносимых отдельными блоками. Для достижения высокой точности прибора требуется высокая стабильность параметров и характеристик каждого из блоков. Все это затрудняет реализацию высокоточных СИ по схеме прямого преобразования.

11.7.3. Уравновешивающее преобразование

Особенность уравновешивающего или, как еще говорят, компенсационного преобразования состоит в том, что выходная величина средства измерений U_вых (рис. 11.24) подвергается обратному преобразованию в величину U'_m, однородную с входной величиной U. Следовательно, используется отрицательная обратная связь.

Средства измерений, имеющие такую структуру, могут работать в двух режимах: неполного уравновешивания, когда сигнал рассогласования U = U_вх - U'_m  О, и полного уравновешивания, когда ди = О. Рассмотрим сначала первый режим.
Цепь прямого преобразования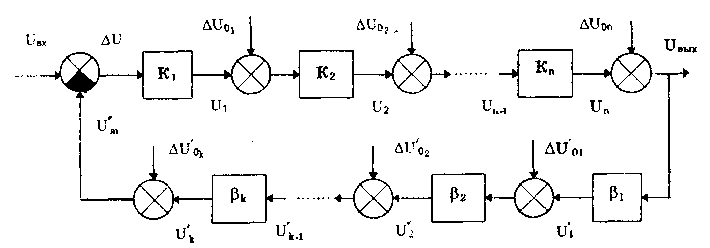



Цепь обратного преобразования
Рис. 11.24. Схема уравновешивающего преобразования
Для вывода уравнения преобразования U_вых = (U_вх) будем считать справедливыми те упрощающие предположения, которые были приняты при анализе схемы прямого преобразования. При отсутствии помех сигнал рассогласования U поступает на вход измерительной цепи прямого преобразования. Ее выходной сигнал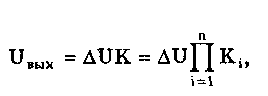



где K_i — коэффициент преобразования i-го структурного элемента цепи прямого преобразования, является входным для цепи обратного преобразования. Ее выходное напряжение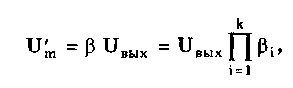



где _i — коэффициент преобразования i-го структурного элемента цепи обратного преобразования.

Коэффициент преобразования СИ с учетом двух последних уравнений имеет вид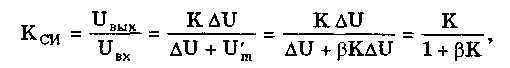



а уравнение преобразования соответственно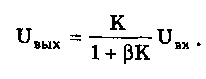

(11.11)

Следовательно, выходной сигнал зависит от коэффициентов преобразования цепей прямого и обратного преобразования. При |ЗК»1 выходное напряжение U_вых  U_вых/, цепь прямого преобразования практически не влияет на работу прибора, поэтому нестабильность коэффициентов преобразования К_i не вызывает погрешности измерения.

Относительная мультипликативная погрешность, обусловленная нестабильностью коэффициентов преобразования К и , находится из уравнения (11.11):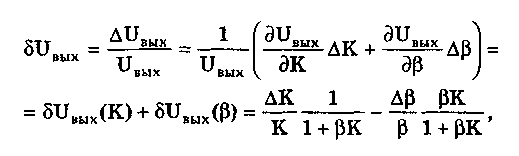



где К,  — суммарные погрешности, обусловленные нестабильностью коэффициентов К и . При К >> 1 погрешность U_вых(K) от нестабильности коэффициентов преобразования прямой цепи уменьшается в (1 + К) раз. Погрешность U_вых(), обусловленная нестабильностью коэффициентов преобразования цепи обратной связи, при этих условиях почти полностью входит в суммарную погрешность. Следовательно, в прямой цепи можно использовать активные нестабильные преобразователи, например усилители, но при этом необходимо выполнять условие К >> 1. Коэффициент обратного преобразования , наоборот, должен иметь высокую стабильность во времени.

Аддитивная погрешность, обусловленная дрейфом нуля, наводками, порогом чувствительности звеньев и другими аналогичными причинами, моделируется путем введения в структурную схему (рис. 11,24) дополнительных сигналов AU₀₁, AU₀₂, …, AU_0n, U'₀₁, U'₀₂,..., U'_0k. Абсолютная аддитивная погрешность, приведенная к входу СИ,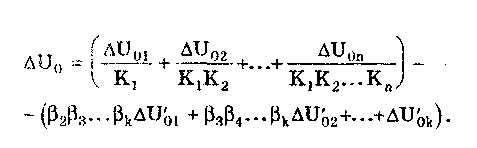



В режиме полного уравновешивания рассогласование U=U—U'_m = 0. Это возможно, если в цепи прямого преобразования имеется интегрирующий элемент с функцией преобразования вида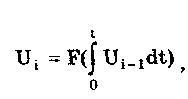



например электродвигатель, интегратор, выполненный на операционном усилителе.

Уравнение преобразования СИ для этого случая имеет вид U_вых = U_вx/. Коэффициент преобразования полностью определяется параметрами цепи обратной связи и не зависит от параметров цепи прямого преобразования.

Мультипликативная относительная погрешность, связанная с нестабильностью коэффициентов преобразования блоков _i,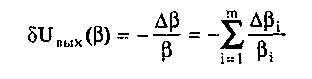



зависит только от свойств цепи обратной связи.

Аддитивная погрешность схем с полным уравновешиванием почти целиком обуславливается порогом чувствительности звеньев U_n — минимальным сигналом на входе, способным вызвать сигнал на выходе (см. рис. 11.23, б). При входном сигнале меньше U_n сигнал на выходе не появляется. Следовательно, уравновешивание схемы наступает при U—U'_m= ± U_n. При этом играет роль порог чувствительности звеньев в цепи прямого преобразования до интегрирующего звена включительно.

Приведенная к входу абсолютная аддитивная погрешность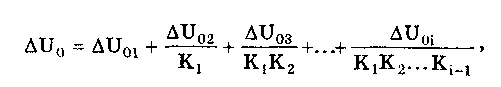



где U_0i - порог чувствительности интегрирующего звена. Для уменьшения погрешности, обусловленной порогом чувствительности звеньев, следует увеличивать коэффициенты преобразования звеньев прямой цепи. В приведенных формулах фигурирует суммарная погрешность — сумма случайной и систематической составляющих.

Схемы СИ зачастую могут быть комбинированными, т.е. содержать цепь прямого преобразования, звенья которой охвачены отрицательной обратной связью. Следует отметить, что принцип построения структурной схемы влияет на многие параметры СИ, такие как входные и выходные сопротивления, динамические и другие характеристики.

11.7.4. Расчет измерительных каналов средств

измерений

Хотя СИ чрезвычайно разнообразны и применяются для измерения самых разных физических величин, назначение у них одно — проведение измерений, поэтому они имеют общую теорию построения. Основными задачами этой теории являются:

• Определение математической модели (ММ) измерительного канала (или цепи) СИ. Модель строится на основе моделей составляющих его структурных элементов. Основной характеристикой, определяемой в процессе моделирования, является уравнение преобразования. При необходимости может рассчитываться одна из полных динамических характеристик СИ, описывающих взаимосвязь его входной и выходной величин в динамических режимах работы. Важно отметить, что часто говорят о ММ средства измерений, подразумевая при этом модель его измерительного канала.

• Расчет метрологических характеристик СИ по метрологическим характеристикам составляющих блоков. При этом могут определяться любые характеристики, однако чаще всего рассчитывается основная погрешность СИ.

Решение второй задачи невозможно без знания математической модели средства измерений, т.е. без решения первой задачи. В общем случае последовательность действий, выполняемых при решении этих задач, состоит в следующем:

1. Разрабатывается структурная схема СИ. Это осуществляется с целью решения поставленной измерительной задачи в соответствии с выбранными принципами и методами измерения на основе имеющейся априорной информации. Важно отметить, что на этом этапе строится идеализированная структурная схема, т.е. схема, в которой не учитываются источники помех и неидеальности составляющих ее элементов. Все это будет учитываться по мере необходимости на последующих этапах расчета. Примером такой схемы является структурная схема термоэлектрического термометра, приведенная на рис. 11.21.

При разработке структурной схемы СИ полезно, а порой и просто необходимо использовать диаграммы, отражающие изменения измерительных сигналов во времени или по частоте. Они существенно облегчают понимание процессов функционирования СИ, особенно цифровых.

В целом ряде случаев перед началом разработки структурной схемы бывает известно уравнение, на основе которого определяется измеряемая величина, например при измерении активной электрической мощности. Данные уравнения фактически являются прообразом, основой ММ измерительного канала СИ, и с их помощью разрабатываются структурные схемы.

2. Производится оценка диапазонов изменения информативных и неинформативных параметров входных и выходных сигналов структурных элементов и СИ в целом. При необходимости могут быть оценены диапазоны изменения влияющих величин. Оценка осуществляется на основе априорной информации об измеряемой величине и условиях измерения.

3. С использованием полученной информации о диапазонах изменения входных и выходных сигналов оцениваются возможности технической реализации структурных элементов и строятся их ММ. При построении моделей должна активно использоваться информация, полученная прикладными техническими науками.

4. Выполняется построение математический модели СИ. При этом используются его структурная схема, ММ составляющих ее элементов, временные и (или) частотные диаграммы измерительных сигналов. Для тех СИ, структурные схемы которых разрабатывались на основе известных уравнений связи измеряемой величины и величин, непосредственно воздействующих на входы приборов, ММ является дальнейшим развитием и уточнением этих уравнений.

Модель представляет собой функцию преобразования СИ, связывающую между собой его входной и выходной сигналы. В качестве независимого аргумента модели может использоваться время или частота изменения измерительных сигналов. Модель измерительного канала СИ может быть описана математической функцией, непрерывной во времени и по размеру. Это характерно для аналоговых СИ. Примером такой ММ является уравнение (11.9), выведенное по структурной схеме, приведенной на рис. 11.21. При моделировании цифровых приборов модель, как правило, является решетчатой функцией, т.е. функцией, дискретной по времени и квантованной по размеру.

5. На основе анализа полученной ММ выделяются элементы структурной схемы, параметры которых в нее входят. Следует помнить, что параметры некоторых структурных элементов измерительного канала могут и не входить в уравнение преобразования. Это прежде всего касается элементов, стоящих в цепи прямого преобразования СИ, реализующих схему уравновешивающего преобразования.

Метрологические характеристики элементов, параметры которых входят в ММ, стараются по возможности определить. К определяемым характеристикам относятся уравнения преобразования, границы, в которых находится систематическая погрешность, дифференциальная функция распределения вероятности случайной составляющей погрешности или ее математическое ожидание и среднее квадратическое отклонение.

6. На этом этапе рассчитывается погрешность СИ по методике обработки результатов косвенных измерений (см. разд. 8.3), а также другие требуемые его метрологические характеристики. При расчете основной погрешности функция преобразования СИ рассматривается как уравнение для определения результатов косвенных измерений, а входящие в него величины — как результаты прямых измерений. Для проведения такого расчета необходимо знать систематические и случайные погрешности каждого из параметров структурных элементов, которые входят в модель измерительного канала СИ.

Расчет погрешностей — наиболее сложная часть расчета СИ, существенно зависящая от количества информации о погрешностях блоков и их характеристиках. Как было показано в 11.7.2 и 11.7.3, погрешность СИ состоит из двух составляющих — аддитивной и мультипликативной. Рассмотрим их „подробнее.

Пусть уравнение преобразования СИ имеет вид у = F(x, a_j, z_i), где х, у — информативные параметры входного и выходного сигналов; z_i = (z₁, z₂, ..., z_k) — влияющие факторы (помехи, наводки, шумы), являющиеся причинами аддитивной погрешности; a_j = (a₁, a₂, ..., a_L) — параметры блоков СИ.

Каждый параметр а_j имеет номинальное значение, при котором вносимая данным блоком погрешность равна нулю. Отклонения реальных свойств элементов от номинальных приводят к возникновению погрешности. Эти отклонения можно условно назвать погрешностями блоков и выразить в виде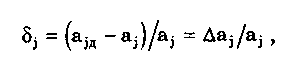



где а_jд — действительное значение параметра блока, а_j — его номинальное значение.

Согласно методике обработки результатов косвенных измерений, погрешность, вносимая j-м блоком в результат измерения у,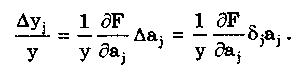



Коэффициент влияния погрешности j-ro блока в относительной форме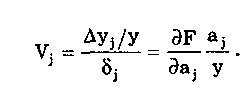



На практике часто уравнение преобразования имеет вид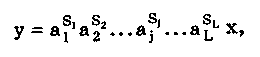



где S_j — положительные и отрицательные натуральные числа. В этом случае коэффициент влияния j-ro блока V_j = S_j.

Коэффициенты влияния для аддитивных погрешностей нельзя выразить в виде отклонения от каких-либо номинальных значений. Поэтому они выражаются в обычной форме: W_i = F/z_i .

Абсолютная погрешность средства измерений при показании у равна сумме мультипликативной и аддитивной составляющих: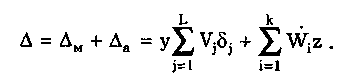

(11.12)

В данном уравнении все погрешности приведены к выходу СИ.

При расчете погрешность оценивается в требуемых точках интервала показаний. Если же известна точка, где погрешность максимальна, то в некоторых случаях можно ограничиться расчетом погрешности для этой точки. Такой точкой в большинстве случаев является конечное значение диапазона показаний у_к, поскольку при этом максимальны мультипликативные составляющие погрешности СИ. Относительная погрешность СИ в этой точке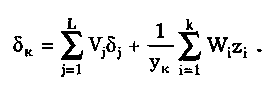

(11.13)

Все погрешности, входящие в правые части формул (11.12) и (11.13), подразделяются на систематические и случайные. Сумма слагаемых, описывающих систематические составляющие, дает систематическую погрешность СИ, а сумма случайных — случайную погрешность. При суммировании последних необходимо учитывать корреляционные связи. С целью упрощения суммирования целесообразно применять критерий ничтожно малой погрешности. Общие правила суммирования погрешностей рассмотрены в гл. 9.

Дальнейшие действия при расчете погрешностей по формулам (11.12) и (11.13) существенно зависят от того, какая информация о погрешностях структурных элементов средства измерений и влияющих факторах имеется в наличии.

Для расчета предельной случайной погрешности при заданной доверительной вероятности Р необходимо знать закон ее распределения. Как показано выше, случайная погрешность СИ определяется суммой случайных погрешностей его блоков, имеющих различные законы распределения. Следовательно, суммарный закон распределения должен определяться как композиция законов распределения ее составляющих. Здесь подчас возникает масса непреодолимых трудностей. Во-первых, законы распределения составляющих, как правило, неизвестны, поскольку для их определения необходимо проводить трудоемкие исследования. Во-вторых, определение композиции законов распределения нескольких слагаемых является весьма трудной математической задачей. В связи с этим часто предполагают, что суммарная случайная погрешность СИ имеет нормальное распределение.

За предельную оценку случайной составляющей погрешности СИ может быть принята величина (Р) = z_pS_, где z_p— квантильный множитель, соответствующий доверительной вероятности Р; S_ — оценка СКО суммарной случайной погрешности. Для практики целесообразно использовать значение Р = 0,95. Если число слагаемых невелико, то вместо квантильного множителя z_p должен использоваться коэффициент Стьюдента t_p. В общем случае значение СКО суммарной случайной погрешности СИ должно рассчитываться по известным правилам (см. разд. 8.3 и 9.3).

Систематические составляющие погрешности СИ определяются в результате детального анализа процессов, протекающих в каждом из блоков, и, как правило, выражаются допустимыми границами. Считается, что они имеют равномерное распределение. В этом случае суммарную систематическая погрешность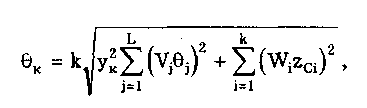



где k — коэффициент, определяемый по табл. 8.4 или 8.5; _j, z_ci — пределы допускаемых систематических погрешностей блоков, образующих мультипликативную и аддитивную составляющие погрешности.

Суммарная погрешность СИ определится по правилам суммирования составляющих, приведенных в разд. 8.3. В общем случае _к = k_P[_k + (Р)] . При перечисленных в табл. 8.6 условиях одной из составляющих можно пренебрегать. Коэффициент k_p определяется по табл. 8.7.

На практике погрешности блоков СИ часто задаются допускаемыми границами _ri и z_ri, включающими как систематическую так и случайную составляющие. В этом случае суммарные погрешности блоков целесообразно рассматривать как погрешности, имеющие равномерные распределения в заданных границах, и складывать их статистически. Суммарная погрешность СИ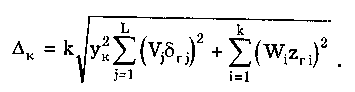

(11.14)

Вычисления погрешностей проводятся для ряда показаний СИ из возможного диапазона измерений. При этом необходимо сохранять неизменной доверительную вероятность, принятую при проведении расчетов. Значения у, при которых производится расчет погрешностей, определяются исходя из следующих соображений. В пределах диапазона изменения измеряемой величины не более десятикратного изменение результирующей погрешности может быть с достаточной степенью точности представлено прямой линией или простейшей кривой. Это позволит описать результирующую погрешность линейной или простейшей нелинейной двузвенной формулой. Если изменение измеряемой величины превышает десятикратное, то весь диапазон разбивается на участки, где и определяются крайние погрешности. Значение аддитивной составляющей характеризует результирующую погрешность в начале диапазона, а сумма значений аддитивной и мультипликативной составляющих в конце диапазона описывает результирующую погрешность в конце диапазона. Если участков несколько, то суммирование проводится на всех участках, а затем принимается решение 6 методе описания результирующей погрешности.

7. Производится расчет измерительного канала СИ, уточняется его структурная схема. Это делается при необходимости более полного учета факторов, влияющих на метрологические характеристики средства измерений. Уточнение структурной схемы осуществляется путем введения в нее источников шумов, дрейфов, наводок и т.п. Кроме того, учетиваются неидеальности структурных элементов.

8. На основании проведенного уточнения схемы СИ производится корректировка его ММ или, если это необходимо, построение новой модели.

9. По уточненной модели СИ производится расчет его основной погрешности и необходимых метрологических характеристик.

Приведенный порядок действий может меняться в зависимости от вида СИ. Чем точнее рассчитываемое СИ, тем более сложным будет построение его модели и расчет метрологических характеристик. Значительные сложности могут иметь место при расчете измерительных каналов цифровых СИ, поскольку приходится моделировать процессы дискретизации во времени и квантования по уровню.
Пример 11.6. Проанализируем структурную схему и рассчитаем канал измерительного преобразователя мгновенного значения периодического сигнала в пропорциональное ему постоянное напряжение. Этот преобразователь, дополненный вольтметром постоянного тока, представляет собой прибор для измерения мгновенных значений переменного сигнала. Сфера применения такого преобразователя довольно широка [95].

Преобразователь реализует компенсационный феррометрический метод, суть которого состоит в том, что среднее за период (начиная с момента t_i) значение интеграла от производной периодической (с периодом Т) нечетной функции X(t) равно отрицательному мгновенному значению этой функции в момент t_i: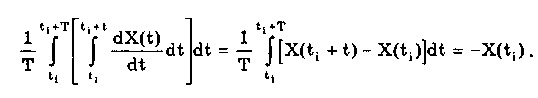

(11.15)

Использование только этой зависимости не дает выигрыша по сравнению с классическим феррометрическим методом [63, 64]. Существенное улучшение метрологических характеристик преобразователя получается, когда в структурную схему, реализующую формулу (11.15), вводится обратная связь. Идеализированная структурная схема такого компенсационного преобразования показана на рис. 11.25. Работой преобразователя управляет устройство управления (УУ), представляющее собой фазовращатель и вырабатывающее управляющие сигналы, которые действуют в течение интервалов времени ₁ = (t_i + nT; t_i + (n+1)Т) и ₂= ₁ + Т= (t_i + (n+l)T); t + (n+l)T + T), где Т  Т. В интервале ₃= (t_i + (n+1)Т + Т; t_i + (n+2)T) все управляющие сигналы не активны. Следовательно, один цикл работы рассматриваемого СИ состоит из трех тактов ₁, ₂ и ₃ и занимает по времени два периода сигнала X(t).

Первичный преобразователь (ПП) преобразует переменный сигнал X(t) в напряжение u_п(t) = К_п dX(t)/dt, где К_п — постоянный коэффициент передачи.

Переменное напряжение u_п поступает на вход интегратора И1. Интегрирование производится в течение интервала ₁, начиная с момента t_i. Выходной сигнал суммируется с проинтегрированным аналогичным образом выходным сигналом компенсационного преобразователя u_n ,(t), полученным на предыдущем (n-1)-м цикле работы. Результирующий сигнал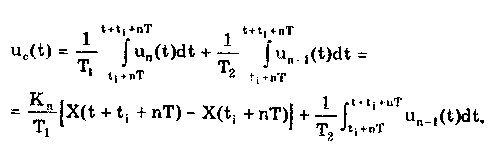

(11.16)

где 0  t  Т; Т₁, Т₂ — постоянные времени интеграторов И1 и И2. Интегратор И2 (равно как и интегратор И1) осуществляет интегрирование сигнала в течение первого такта работы ₁. Во втором и третьем тактах работы они оба сброшены управляющим сигналом и их выходные сигналы равны нулю. Это также устраняет погрешность, вносимую дрейфом нуля интеграторов.

Поскольку выходной сигнал данного преобразователя является постоянным (это будет видно из дальнейшего изложения), то при "включении" интегратора И2 в момент t_i + nT сигнал u_n-1(t) можно представить в виде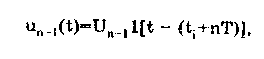

(11.17)

где U_n-1 — значение постоянного напряжения на выходе запоминающего интегратора И4 на предыдущем цикле работы; l[t - (t_i - nT)] — единичная функция. При этом выражение (11.16) с учетом (11.17) запишется в виде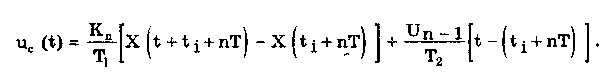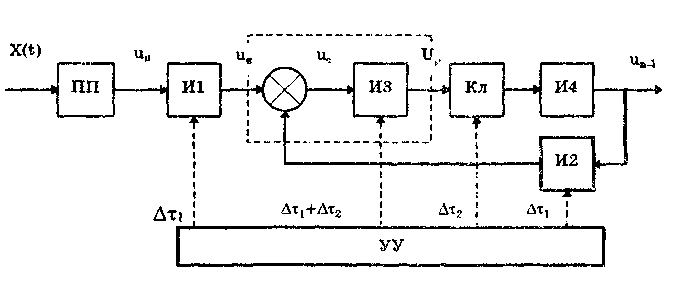





Рис. 11.25. Структурная схема компенсационного преобразователя

Данный сигнал действует на входе интегратора ИЗ в течение первого такта работы Дт_г В остальных тактах Дт₂ и Дт₃ он равен нулю. Сам нее интегратор ИЗ находится в активном, интегрирующем режиме весь второй такт Дт^Д^+ДТ. Следовательно, после интегрирования сигнала u_c(t) в течение времени AT сигнал на его выходе будет постоянен и имеет вид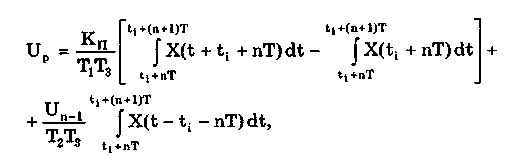



где Т₃ — постоянная времени интегратора ИЗ. Интеграл от X(t + t_i+ nT) равен нулю при периодической нечетной функции X(t). С учетом этого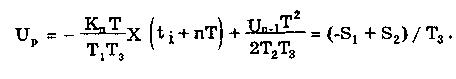

(11.18)

Из уравнения (11.18) видно, что на выходе интегратора ИЗ формируется сигнал, пропорциональный разности вольт-секундных площадей S₂ и S₁. Следовательно, сумматор и интегратор ИЗ образуют вычитающее устройство (на рис. 11.25 обведено штриховой линией), формирующее сигнал рассогласования для цепи внутреннего прямого преобразования. Сигнал U_p действует на выходе интегратора ИЗ в течение интервала ₂. В остальную часть (n+1)-го периода (₃) он сбрасывается управляющим сигналом и его выходное напряжение равно нулю.

Сигнал рассогласования U_p поступает на интегратор И4 в течение второго такта работы ₂ через открытый ключ Кл. При условии, что коэффициент передачи ключа равен единице, выходное напряжение преобразователя с учетом (11.18) имеет вид "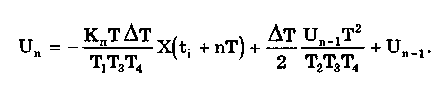



В установившемся режиме U_n-1 = U_n, и, значит, их разность равна нулю. Тогда из последнего уравнения следует, что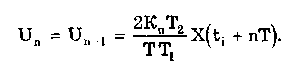

(11.19)

Таким образом, в установившемся режиме работы выходное напряжение компенсационного преобразователя постоянно и прямо пропорционально мгновенному значению измеряемой физической величины X(t_i). Изменяя с помощью УУ моменты времени t_i, можно проводить преобразование и последующее измерение любого мгновенного значения исследуемого сигнала X(t).

В уравнение преобразования (11.19) входят только параметры блоков (первичного преобразователя и интегратора И1), стоящих в цепи прямого преобразования до контура компенсационного преобразования, а также интегратора И2, стоящего в цепи обратной связи. Следовательно, погрешность преобразования мгновенных значений X(t_i) в постоянное напряжение состоит из погрешности, вносимой первичным преобразователем, и погрешности, связанной с точностью выполнения операций интеграторами И1 и И2. При этом случайная аддитивная погрешность, обусловленная дрейфом нуля на их выходах, практически равна нулю вследствие ключевого режима работы, а погрешность от нестабильности постоянных времени существенно ослаблена.

Запишем уравнение (11.19) в виде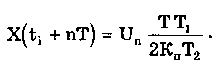

(11.20)

Уравнение (11.19) или (11.20) является математической моделью рассматриваемого измерительного компенсационного преобразователя. Ска описывает во многом идеализированный измерительный канал и не учитывает неидеальности структурных элементов и влияние факторов z_i, которые являются источниками аддитивных погрешностей. В связи с этим суммарная погрешность преобразователя будет содержать только мультипликативные составляющие, обусловленные неточностями задания и нестабильностями периода переменного сигнала Т и постоянных времени T_t, T₂, а также неточностью задания коэффициента передачи К_п преобразователя ПП.

Будем считать, что нам известны систематическая и случайная составляющие первой и второй погрешностей и только систематическая составляющая третьей погрешности. В простейшем случае погрешности, вносимые блоками преобразователя, могут быть заданы допускаемыми границами _гi, включающими как систематическую, так и случайную составляющие и имеющими равномерные распределения. Из уравнений (11.14) и (11.19) легко получить, что абсолютная погрешность преобразования мгновенного значения сигнала X(t) в напряжение U_n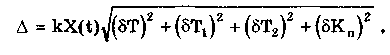



где Т, Т₁, Т₂, К_П — допускаемые границы погрешностей задания периода измеряемого сигнала X(t), постоянных времени интеграторов И1 и И2, коэффициента преобразования первичного преобразователя соответственно; k — коэффициент, определяемый по табл. 8.4.

Предположим, что в нашем распоряжении имеется более полная информация о погрешностях блоков рассматриваемого измерительного преобразователя, а именно, известны: оценки СКО случайных погрешностей периода переменного сигнала S_T, постоянных времени S_T1 и S_T2, а также пределы (границы) систематических погрешностей периода _Т, постоянных времени _Т1, _Т2 и коэффициента передачи первичного преобразователя _Кл.

При реализации структурной схемы (см. рис. 11.25) интеграторы И1, И2 и сумматор выполняются в виде интегратора-сумматора на одном операционном усилителе. В связи с этим резистивные и емкостный элементы, определяющие значения постоянных времени T₁ и Т₂, располагаются в пространстве рядом и подвержены практически одинаковым возмущающим воздействиям, обуславливающим случайную погрешность. Все это приводит к тому, что случайные погрешности обеих постоянных времени сильно коррелированы (коэффициент корреляции близок к единице) и должны складываться по формуле (9.12), т.е. S_T12 = S_T1 + S_T2 .

Случайные погрешности задания периода переменного сигнала и постоянных времени никак не связаны между собой (коэффициент корреляции близок к нулю) и, следовательно, должны складываться геометрически в соответствии с формулой (9.13):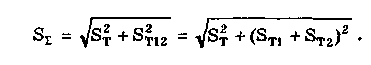



Доверительный интервал суммарной случайной составляющей погрешности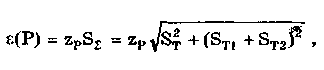



где z_p — квантильный множитель суммарного закона распределения случайной погрешности, соответствующий доверительной вероятности Р. Для расчета его значения могут быть использованы формулы, приведенные в разд. 9.1.

Суммарная систематическая погрешность измерительного преобразователя при X(t) = X(t_k) имеет вид: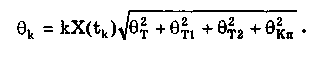



Множитель k зависит от принятой доверительной вероятности, соотношения между слагаемым и определяется по табл. 8.4.

Суммарная погрешность измерительного преобразователя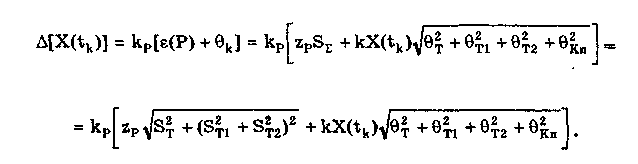



Коэффициент k_p зависит от соотношения суммируемых случайной и систематической составляющих и определяется по табл. 8.7.
Контрольные вопросы.
1. Что такое средство измерений?

2. Назовите статические характеристики и параметры средств измерений.

3. Что такое функция преобразования средства измерений? Какие виды функций преобразования используются в метрологии?

4. Назовите динамические характеристики и параметры средств измерений.

5. Что такое полоса пропускания средства измерений и как она связана с амплитудно-частотной характеристикой?

6. Каким образом классифицируются средства измерений?

7. Какие средства измерений относятся к элементарным? Какие функции они выполняют? Почему они называются элементарными?

8. Какие типы измерительных преобразователей вы знаете? Для чего предназначены аналого-цифровой и цифро-аналоговый преобразователи?

9. Из чего состоит аналоговый измерительный прибор? Как устроены применяемые в них отсчетные устройства?

10. Из каких структурных элементов состоит цифровой измерительный прибор? Чем он отличается от аналогового измерительного прибора?

11. Что такое измерительно-вычислительные комплексы? Как они устроены?

12. Для чего необходимо моделировать средства измерений? Что такое математическая модель средства измерений? Какие величины она связывает между собой?

13. Дайте определение следующим понятиям: измерительная цепь, измерительный канал, структурный элемент и структурная схема.

14. Приведите примеры известных вам структурных элементов. Запишите их уравнения преобразования.

15. Перечислите этапы расчета измерительных каналов средств измерений.