Токсик. Предмет теории вероятностей. Случайное событие. Виды событий. Вероятность событий. Классическая и статистическая вероятности событий
 Скачать 5.51 Mb. Скачать 5.51 Mb.
|
|
Билет №1 Предмет теории вероятностей. Случайное событие. Виды событий. Вероятность событий. Классическая и статистическая вероятности событий. Теория вероятностей – это раздел математики, который изучает закономерности, присущие случайным событиям массового характера. Под «событием» в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти. Вероятность события есть численная мера степени объективной возможности этого события. Вероятность достоверного события - такого события, которое в результате опыта непременно должно произойти. Противоположностью по отношению к достоверному событию является невозможное событие - такое событие, которое в данном опыте не может произойти. Таким образом, установлены единица измерения вероятностей – вероятность достоверного события - 1. Виды событий. Несовместимые события, если при испытании появление одного из них исключает появление другого. События называются совместимыми в данном опыте, если они могут произойти одновременно. Независимые события, если появление одного из них не зависит от появления другого. Зависимые события, если появление одного из них зависит от того, произошло другое в условиях данного опыта. Противоположными называются события, если появление одного из них, исключает появление другого. Единственно возможное событие – если в условиях опыта произойдет только это событие. Существуют 2 определения вероятности события: Классическая вероятность события вычисляется как отношение числа благоприятных случаев к общему числу случаев: Р(А) = m/n, где Р(А) – вероятность события А; n – общее число случаев; m – число случаев, благоприятных событию А. Если Р(А) = 0 – событие невозможное, если Р(А) = 1 – событие достоверное. Классическое определение можно применять лишь, когда число элементарных исходов конечно. Статистическая вероятность события применяется в случае, когда число испытаний n стремится к ∞: P*(A)=lim m/n , n→∞ Статистические критерии. Виды критериев. Ск — это решающее правило, обеспечивающее надежное поведение, т е принятие истинной и отклонение ложной гипотезы с высокой вероятностью. Ск рассчитывается по определенной формуле в зависимости от частоты встречающего признака - эмпирическое (фактическое) значение Ск - случайная величина и подчиняется законам распределения Зная объем выборки n число степеней свободы k, опред по табл критерием (стандартное) значение критерия и сравниваем с эмпирическим.   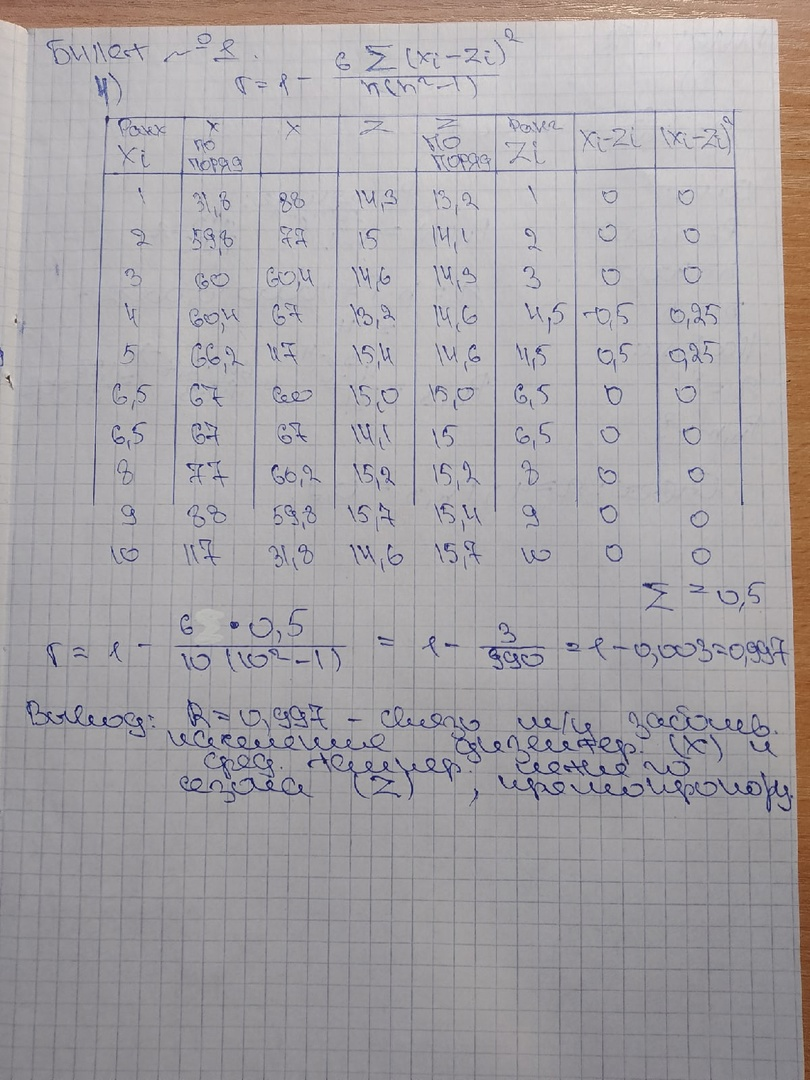 Билет №2 Операции над событиями. Сложение событий. Вероятность суммы двух событий. Вероятность противоположного события. Суммой 2-ух событий А и В является событие С, которое заключается в появлении либо события А, либо события В, либо их совместном проявлении: A+B=C Вероятность одного из двух несовместимых событий равна сумме вероятностей этих событий: Р(А+В) = Р(А) + Р(В) Вероятность одного из двух совместимых событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В) = Р(А) + Р(В) – Р(А*В). Параметрические критерии. Проверка гипотезы относительно средних. t-критерий Стьюденса.     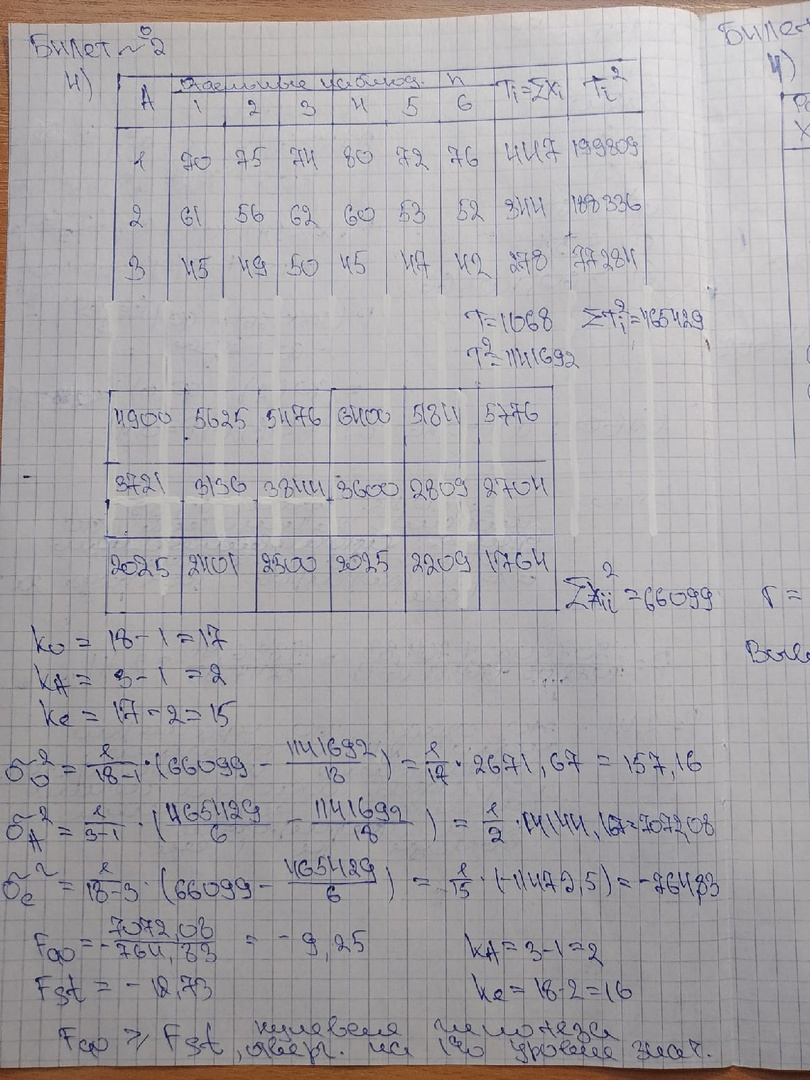  |
