Биостатистика. биостат рк1-1. предметом, методологией, понятиями и категориями
 Скачать 37.09 Kb. Скачать 37.09 Kb.
|
|
Статистика изучает: +массовые явления любой природы Чем отличается статистика от других наук: +предметом, методологией, понятиями и категориями. Предметом изучения статистики являются статистические: совокупности. Статистическая совокупность – это: +любые изучаемые массовые явления Какими свойствами должна обладать статистическая совокупность: +множеством качественно однородных единиц, которым свойственны варьирующие признаки, подлежащие регистрации и изучению Статистическая методология включает: +методы сбора и систематизации данных, исчисления и анализа данных Статистическое исследование включает: +статистическое наблюдение, группировку и сводку, обработку и анализ данных Проводится обследование состояния здоровья подростков. Единицей наблюдения является: Формами статистического наблюдения являются: отчетность и специальные статистические обследования Дискретные группировочные признаки – это: + вариационные Непрерывные признаки могут иметь: +любые значения в некотором интервале Признак – это: +характеристика (качественная особенность) единицы совокупности Статистика изучает признаки, которые: +количественние и атрибутивные Статистический расчет представляет собой: + исчисление статистических показателей Статистический показатель – это: +обобщающая характеристика какого-то свойства отдельных единиц, группы единиц или совокупности в целом Статистическая таблица – это: наглядное изложение (представление) в специальной (табличной) форме статистического материала Количественные признаки могут быть представлены: + соответствующим размером и единицей измерения (численность населения, масса прибыли, средняя заработная плата) Атрибутивные признаки – это: +описательные Ряд (закон) распределения – это: + единицы совокупности, расположенные в порядке возрастания или убывания значений признака Полигон – это: + график дискретного ряда распределения Гистограмма – это: + график интервального ряда распределения Ряды распределения называются вариационными: + построенные по количественному признаку Под ранжированием понимают: + расположение всех значений в возрастающем (или убывающем) порядке Какой показатель в статистике называется абсолютной величиной: + показатель, который имеет физические единицы измерения Относительные величины – это: + отношение двух статистических величин Средняя величина – это: + обобщенная типическая характеристика признака в данной совокупности Для расчета общей средней по сгруппированным данным следует применить формулу средней: арифметической взвешенной Мода в ряду распределения – это: + значение признака, встречающееся чаще всего; Медиана в ряду распределения – это: +значение признака, делящее ряд распределения на две равные части; Вариация – это: + изменчивость (отклонение) индивидуальных значений признака по единицам совокупности Для измерения вариации значения признака применяются следующие статистические показатели: + размах вариации, среднее линейное отклонение, дисперсия, среднеквадратическое отклонение, коэффициент вариации Ошибки репрезентативности возникают при: + не сплошном наблюдении Если все значения признака увеличить на некоторую постоянную величину, то средняя арифметическая: + увеличится на эту величину Если все значения признака умножить на некоторую постоянную величину, то средняя арифметическая: + увеличится во столько раз Если все значения признака увеличить на некоторую постоянную величину, то дисперсия: + не изменится Если все значения признака увеличить в 10 раз, то дисперсия: + увеличится в 10 раз Для сравнения вариации двух различных признаков необходимо использовать: + коэффициент вариации Ошибки репрезентативности возникают при: + не сплошном наблюдении В чем преимущества выборочного наблюдения перед сплошным: + экономия на материалах и денежных затратах При формировании выборочной совокупности соблюдение принципа случайности: +обязательно Как определяются границы возможных значений генеральной средней: + Выборочная средняя плюс (минус) предельная ошибка выборочной средней; Статистическая гипотеза – это: +Предположение, которое можно проверить с использованием имеющейся статистической информации; Критерий – это: +Набор правил, принимаемых для проверки статистической гипотезы; Мощность критерия представляет собой: + Способность критерия четко различать нулевую и альтернативную статистические гипотезы; Ошибка первого рода – это: + отклонение статистической гипотезы, когда она правильна; Ошибка второго рода – это: + принятие статистической гипотезы, когда она ошибочна; Уровень значимости – это: +вероятность, соответствующая отклонению верной гипотезы; Величина, которая в результате испытания примет одно и только одно возможное значение неизвестное заранее. + Случайная Таблица, в которой указаны возможные значения случайной величины и их вероятности. + Закон распределения Значение участка площади под кривой Гаусса, соответствующий промежутку от ‹ х › - δ < х < ‹ х › + δ. +0,683 На практике можно полагать, что фактически все значения рассматриваемой случайной величины находятся в пределах промежутка, простирающегося + ‹х›–3σ до ‹ х›+3σ Дан закон распределения дискретной случайной величины. Найти ее дисперсию.
+ 1,44 Дисперсия дискретной случайной величины равна 9, вычислить ее среднее квадратическое отклонение +3 Среднее квадратическое отклонение дискретной случайной величины равно 3,1. Найти дисперсию этой величины. 9,61 Закон распределения дискретной случайной величины задан таблицей. Найти ее моду.
1 Случайная величина, принимающая отдельные друг от друга возможные значения с определенными вероятностями, которые можно пронумеровать. дискретная Среднее квадратическое отклонение дискретной случайной величины равно 1,5. Найти дисперсию этой величины. 2,25 Коэффициент, который зависит от числа степеней свободы f и доверительной вероятности. коэф Стьюдента Интервальной оценкой математического ожидания является: доверительный интервал В математической статистике отношение суммы значений признаков к общему числу признаков: арифметическое среднее Среднее арифметическое квадратов отклонения значений признаков от их выборочной средней: дисперсия Случайная величина, принимающая все значения из некоторого конечного или бесконечного интервала: непрерывная Квадратный корень из дисперсии среднее квадратическое отклонение Совокупность, состоящая из всех объектов, которые могут быть к ней отнесены. + генеральная Основоположник современной прикладной статистики и математической генетики. Рональд Фишер Множество объектов, случайно отобранных из генеральной совокупности. выборка Число объектов, генеральной совокупности. Объем Наблюдаемые значения признака. Варианта Последовательность вариант, записанная в возрастающем (убывающем) порядке. Вариационный ряд, ранжированный ряд Соответствие между возможными значениями случайной величины и их вероятностями. +Закон распределения случайных величин Законом распределения обычно называют … в которой случайные величины расположены в порядке возрастания или убывания. таблицу Оценка характеристик генеральной совокупности определяемая одним числом. Точечная Множество точечных оценок, определяемых числом наблюдений называют… . + Интервальной Точечная оценка должна удовлетворять следующим требованиям, быть: При исследованиях в фармации, медицине и биологии доверительную вероятность принимают равной... . +0,95% 0,05% При разработке стандартов доверительную вероятность принимают равной... . +0,99 Чтобы найти ширину интервала, нужно знать: Ошибка второго рода: Не отбрасывание нулевой гипотезы, когда она ложна Ошибка первого рода: Отбрасывание нулевой гипотезы, когда она верна Нулевая гипотеза ( 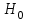 ): +Утверждение, которое не предполагает обнаружения влияния вмешательства в популяции ): +Утверждение, которое не предполагает обнаружения влияния вмешательства в популяции Величина отдельной переменной, которая наиболее часто появляется в группе данных + Мода Признак, который регистрируется для каждого из объектов, называют: +переменной Данные по их типу делятся на:количественные и качественные С количественными данными можно выполнять все обычные операции над числами, такие, как: вычисление среднего и оценку изменчивости В зависимости от того, какие значения может потенциально принимать переменная, выделяют два типа количественных данных: дискретные и непрерывные. Переменная, которая может принимать значения только из некоторого списка определенных чисел. +дискретная 109. К какому типу переменных относится число детей в семье; число вызовов "скорой помощи", поступающих в больницу и т. п. + Дискретной Переменная, принимающая любые значения из некоторого промежутка. Непрерывная Рост взрослого человека (например от 140 до 230 см), фактическая масса буханки хлеба (например от 750 до 830 г) и т.п. является примером … переменной. +Непрерывной Данные, которые регистрируют определенное качество, которым обладает объект. +Качественные К полу человека приписываются соответственно числа 0 и 1. эти числа обрабатываются как … +качественные Впервые ввел в употребление слово «biometry» и разработал основы корреляционного анализа. +Френсис Гальтон Медианой называется: +варианта находящаяся в середине ряда Средняя масса таблетки при девятикратном измерении получилось 0,528 г. средняя квадратическая ошибка (0,014) и коэффициент Стьюдента (2,262) при надежности 0,95. Как записать окончательный результат измерений? 0,528+-0,014. Показатели меры разброса вариационного ряда дисперсия, средне-квадратическое отклонение, стандартное отклонение, коэффицент вариации, квартильный размах Основное свойство выборки:репрезентативность то есть корректно отражать генеральную совокупность Для медико-биологических исследований преимущество вероятности безошибочного прогноза:95% Что означает доверителный интервал? приблизительный диапазон значений, который с высокой степенью вероятности включает все данные (результаты) Эксцесс нормального распределения равен: +нулю Уровень значимости – это +вероятность справедливости нулевой гипотезы при условии ее отвержения Качественные признаки подразделяют на: альтернативные, атрибутивные и порядковые признаки Дана выборка: 5, 2, 9, 2, 8, 5, 4, 8, 10, 12, 13, 15. Определите обьем выборки:12 Качественные признаки не могут быть изменены, и числовыми оценками для них является. … +частота встречаемости Вид качественных данных, которые после сбора были упорядочены по какому-то принципу, например распределение пациентов, по стадиям заболеваний – I, II, III и т.д. стадия Упорядоченные данные Проверяет нулевую гипотезу, что среднее значение группы разностей парных наблюдений равна нулю Парный t критерий Критерий проверки гипотез, который не делает предположений о распределении анализируемых данных. Иногда называется критерий, свободный от распределения, или ранговый метод непараметрический критерий Исследует, отличается ли средняя переменной от некоторой гипотетической величины +Одновыборочный t-критерий (Стьюдента) Чему равна сумма всех относительных частот для выборки?- сумма всех относительных частот равна единице Значение уровня значимости α, которое часто используется на практике Основным условием применения параметрических методов анализа является: +нормальное распределение признака Какое из приведенных ниже требований к выборочной совокупности является основным: +репрезентативность Объект наблюдения, это: явление, подлежащее исследованию Некоторые критерии могут применяться только в том случае, если известно, что переменные подчиняются конкретному закону распределения, например нормальному закону. Эти критерии называют: + Параметрическими Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке, то используете: + t-критерий для зависимых выборок Что такое «нижний квартиль»? это 25-й персентиль: значение признака, которое делит распределение на 25% и 75%, четверть значений меньше нижнего квартиля, три четверти – больше Что такое «верхний квартиль»? это 75-й персентиль: значение признака, которое делит распределение на 75% и 25%, т.е. три четверти значений меньше верхнего квартиля, четверть – больше Для графического представления распределений непрерывно варьирующих признаков используется … .гистограмма Острота пика распределения характеризуется: эксцессом Основной метод обработки статистических данных: выборочный метод; Дана выборка: 1, 2, 10, 2, 8, 5, 4, 7, 7. Обьем равен: 9 Для установления числа групп интервального статистического ряда распределения используют формулу: формуле Стерждесса Площадь гистограммы частот равна. - объему выборки, а площадь гистограммы частостей равна 1 (сумме всех частот, т.е. объему выборки) Получены следующие результаты: 15; 14; 9; 12; 17 и 11. Найдите среднее значение.13 При проверке гипотезы получено,что значение U-критерию Манн-Уитни Uвыч= 15, критическое значение U0,05=10 сделайте вывод относительно гипотезы с 1% ошибкой допускается Н0 В каких случаях применяются непараметрические критерии проверки статистических прогнозов? Распределение не соответствует нормальному или если распределение неизвестно и его нельзя проверить или если признаки качественные Непараметрический критерий, сравнивающий парные наблюдения +Критерий знаковых рангов Вилкоксона. В каких случаях применяется U-критерий Манн-Уитни для проверки статистических гипотез? непараметический статистический критерий, используется для оценки различий между двумя независимыми и несвязанными малыми выборками по уровню какого-либо признака, измеренного количественно В каких случаях применяется U-критерий Манн-Уитни для проверки статистических гипотез? непараметический статистический критерий, используется для оценки различий между двумя независимыми и несвязанными малыми выборками по уровню какого-либо признака, измеренного количественно Если вы хотите сравнить две переменные, которые относятся к двум выборкам, то существуют альтернативные не параметрические тесты: критерий знаков и критерий Вилкоксона парных сравнений. При использовании критерия предполагаемой проверки гипотез на уровне значимости 0,05 значения р=0,06023. Сделайте вывод принимается Н0 После проверки статистического предположения на заданном уровне значимости α=0,05 исследователь имеет вероятность р=0,02. Какую гипотезу нужно принять исследователю? Альтернативная гипотеза Исследовалось проницаемость сосудов сетчатки у здоровых и больных людей. Уровень значимости α=0,05. Результаты расчета критерия Манна-Уитни U=19; р=0,002. Необходимо сделать вывод о статистической значимости полученных различий. Проницаемость сосудов сетчатки статистически значимо различается у групп с вероятностью не менее 95% При проверке гипотезы получено, что значение U-критерию Манн-Уитни Uвыч= 3, критическое значение U0,05=6 сделайте вывод относительно гипотезы Н1 принимается и следовательно значения различные ??Если р=0,03, а α=0,01, то какая гипотеза принимается: При проверке гипотезы получено, что значение U-критерию Манн-Уитни Uвыч= 2, критическое значение U0,05=0 сделайте вывод относительно гипотезы принимается нулевая гипотеза,следовательно значения одинаковые и считается статистически незначимым В каких случаях применяется Т-критерий Уилкоксона для проверки статистических гипотез? Выборка является зависимым, и исследуемый признак количественный и закон распределения неизвестен В каких случаях применяется Т-критерий Уилкоксона для проверки статистических гипотез? Выборка является зависимым, и исследуемый признак количественный и закон распределения неизвестен Непараметрический тест для сравнения показателей до и после: Когда выборка является зависимым и используется критерий Уилкоксона При проверке гипотезы получено, что значение Т-критерий Уилкоксона Твыч =8; Ткрит0,05=13; Сделайте вывод относительно гипотезы принимается альтернативная гипотеза и следовательно значение после изменяется с вероятностью не менее 95% При проверке гипотезы получено, что значение U-критерию Манн-Уитни Uвыч= 15, критическое значение U0,05=10 сделайте вывод относительно гипотезы принимается нулевая гипотеза и следовательно значение одинаковые и считается статистически незначимым Дан закон интервального статистического ряда распределения, вычислите относительные частоты:
0,1; 0,2; 0,4; 0,2; 0,1 Дан закон интервального ряда распределения. Чему равен объем выборки?
20 Определите степень распределения f (степени свободы), если n1 = 15, n2=25 14,24 К ранговым критериям относится критерий Уилкоксано и Манна-Уитни Значения U-критерия Манна-Уитни равны 29 и 15. Какое из значений U выбирают в качестве критерия: 15 Экспериментальное значение критерия Уилкоксона равно 8. По таблице критическое значение критерия равно 9. Принимается: Н0 Объем выборки равен 16, если будет известно, что среднее квадратическое отклонение равно 64, то найдите значение стандартной ошибки: 4 В исследовании влияния некоторого препарата на 15 добровольцах измерялось содержание железа в крови. Какой критерий можно использовать для выяснения влияния препарата на содержание железа в крови, если известно, что исследуемый признак имеет нормальное распределение?параметрический критерий стьюдента зависимые выборки В группе из 6 человек изучалось влияние пробежки на ЧСС (уд/мин). Измерялось ЧСС до пробежки и после пробежки. Распределение выборки не известно, выберите критерий проверки гипотезы:непараметрический критерий Уилкоксона зависимые выборки В группе из 6 человек изучалось влияние пробежки на ЧСС (уд/мин). Измерялось ЧСС до пробежки и после пробежки. Если распределение выборки нормальное, выберите критерий проверки гипотезы: параметрический критерий Стьюдента(зависимая выборка) |
