ответф. +предметом, методологией, понятиями и категориями. предметом, методологией, понятиями и категориями
 Скачать 307.23 Kb. Скачать 307.23 Kb.
|
|
219. При большом объеме выборки ее элементы объединяют в группы согласно следующим действиям: определяют количество интервалов; 4) определяют частоты — количество ni элементов выборки, попавших в iй интервал. ; 2) вычисляют ширину (шаг) интервала;1) находят max и min значения выборки; Все 222. Таблица содержащая в верхней строке элементы выборки или середины интервалов группировки, а в нижней — частоты ni представляет собой. … статистический ряд 223. Частота повторения отдельных значений признаков. накопленная частота 224. Число интервалов зависит от объема выборки 225. Площадь ступенчатой фигуры над графиком гистограммы равна … . объему выборки. 226. Для графического представления распределений непрерывно варьирующих признаков используется … .гистограмма 227. На практике полигон накопленных частот используется в основном для представления: дискретных данных 228. Важным способом "описания" переменной является … …, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Форма ее распределения 229. У симметричного распределения асимметрия равна: 0 230. Острота пика распределения характеризуется: эксцессом 231. Основной метод обработки статистических данных: выборочный метод; 232. Размах выборки это: max значение минус min значение (разность между максимальным и минимальным значениями элементов выборки.) 233. Что является исходным материалом для статистического исследования: выборка; 234. Дана выборка: 1, -2, 10, -2, 8, -5, 4, 7. Объем выборки равен:8 235. Совокупность всех исследуемых объектов называют:Генеральная совокупность 236. Совокупность случайно отобранных объектов из генеральной совокупности. выборка 237. Дана выборка 118, 121, 115, 125, 125, 117, 120, 119 размах выборки равен: 10 238. Для установления числа групп интервального статистического ряда распределения используют формулу: формуле Стерждесса 239. В случае, когда число значений признака Х велико или признак является непрерывным, составляют.- интервальный ряд 240. Гистограммой частот (частостей) называется.-ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы, длина которых равна h, а высоты равны плотности частоты. 241. Площадь гистограммы частот равна. - объему выборки, а площадь гистограммы частостей равна 1 (сумме всех частот, т.е. объему выборки) 242. Задача выборочного метода: оценка параметров (характеристик) генеральной совокупности по данным выборки. 243. Дан закон интервального ряда распределения. Вычислите относительные частоты.
0,1; 0,2; 0,4; 0,2; 0,1 244. Дан закон интервального ряда распределения. Чему равен объем выборки?
20 246. Как называется интервал, где расположено среднее арифметическое значение генеральной совокупности по заданной доверительной вероятности? -доверительный интервал 247. Оценка доверительного интервала малой выборки:- Среднее квадратическое отклонение 248. Изменение количественных значении изучаемого признака статистической . совокупности при переходе на следующую варианту: -вариация 250. Получены следующие результаты: 99,9 %; 99,8 %; 99,6 %; 99,1 %; 99,2 % и 99,2 % .. Найти среднее значение. 99,5% 252. Соответствие между возможными значениями случайной величины и их вероятностями.- закон распределения случайной величины 253. Количественное значение изучаемого признака статистической совокупности: -варианта 254. Таблица, содержащая значения вариант и их частоты: вариационный ряд или таблица частот 255. Чему равна сумма всех относительных частот для выборки?- сумма всех относительных частот равна единице 256. Точечная оценка параметра называется ... , если ее среднее значение равно оцениваемому параметру. - несмещённый 257. Точечная оценка параметра называется ... , если ее среднее значение не равно оцениваемому параметру. -Смещённой При корреляционной факторной связи каждому значению факторного признака соответствует: множество значений результативного признака. Для выявления наличия связи между признаками можно использовать: в) методы параллельных построений, построения корреляционных таблиц, группировки и исчисления групповых средних, построения корреляционного поля. Для оценки степени тесноты связи при линейной зависимости используется: корреляционное отношение; Мерой степени тесноты связи для нелинейной формы зависимости является: корреляционное отношение; Коэффициент корреляции рангов Спирмена можно применить для оценки тесноты связи между: качественными признаками, проявления (значения) которых можно упорядочить; Вид уравнения, характеризующего корреляционную связь, можно обосновать с использованием: регрессионного анализа; Для оценки параметров уравнения регрессии можно применить: б) метод наименьших квадратов; Разработчик основ множественной регрессии, теории сопряженности признаков, а также основ нелинейной корреляции и регрессии. Пирсон Специфическая совокупность приемов, которая предназначена для изучения причин возникновения и распространения любых патологических состояний в популяции людей эпидемиологический метод Научная основа профилактической медицины, так и источник информации для проведения мероприятий в области здравоохранения. эпидемиология Методы Анализа выживаемости в основном применяются к тем же статистическим задачам, что и другие методы, однако их особенность в том, что они применяются: к цензурированным или, как иногда говорят, неполным данным Количество впервые диагностированных случаев данного заболевания в течение определенного периода времени. Заболеваемость Заболеваемость, деленная на общее время воздействия вредного фактора для всей исследуемой группы населения характеризует. уровень заболеваемости Мера риска заболевания Вероятность заболевания Точка на временной оси, в которой кумулятивная функция выживания равна 0.5. Медиана ожидаемого времени жизни Если вы имеете несколько групп, то можете использовать дисперсионный анализ Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке, то альтернативными непараметрическими тестами являются: критерий знаков и критерий Вилкоксона парных сравнений. Рассматриваемые переменные по природе своей категориальны или являются категоризованными (т.е. представлены в виде частот попавших в определенные категории), то подходящим будет критерий хи квадрат макнемара Если рассматривается более двух переменных, относящихся к одной и той же выборке, то используется дисперсионный анализ (ANOVA) с повторными измерениями. Для того, чтобы оценить зависимость (связь) между двумя переменными, обычно вычисляют коэффициент корреляции Пирсона. Отдельный вид ANOVA, применяемый для сравнения средних двух и более независимых групп наблюдений Однофакторный дисперсионный анализ Если порядок записи значений данных во времени имеет содержательный смысл, то говорят, что эти данные представляют собой … . временной ряд. Вид качественных данных, которые после сбора были упорядочены по какому-то принципу, например распределение пациентов , по стадиям заболеваний – I, II, III и т.д. стадия. Упорядоченные данные Зависимость количественной переменной от нескольких качественных (например, как пол, отношение к курению, цвет волос влияют на САД) можно изучить с помощью – гипотезы об однородности средних дисперсионного анализа Вероятность развития у человека болезни в течение определенного периода. Риск Когортное исследование, непараметрический подход к сравнению двух кривых выживаемости Логранговый критерий Метод оценки параметров в регрессионном анализе. Метод наименьших квадрантов Параметры (например, наклон и пересечение в парной регрессии), которые описывают уравнение регрессии Коэффициенты регрессии Наиболее естественным способом описания выживаемости в выборке является построение … . Таблиц времен жизни Надежность оценки выживаемости, в основном зависит от … . количество исходного материала, объема выборки Общий термин для методов, которые сравнивают средние значения групп наблюдений путем расщепления общей дисперсии переменной на ее компоненты. Дисперсионный анализ (ANOVA) Изучение влияния одного или нескольких факторов на рассматриваемый признак. Однофакторный дисперсионный анализ Когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений, используется однофакторный дисперсионный анализз Для независимых выборок предполагают, что они имеют разные выборочные средние и одинаковые выборочные дисперсии. Поэтому, чтобы ответить на вопрос, оказал ли некоторый фактор существенное влияние на разброс выборочных средних или разброс является следствием случайностей, вызванных небольшими объемами выборок, необходимо провести … .однофакторный дисперсионный анализ Укажите правильную последовательность вычислений, при однофакторном дисперсионном анализе: 3, 4,5, 1, 2,6 1) Дисперсию с k-1 степенями свободы; 2)Дисперсию с N - k степенями свободы; 3) Сумму квадратов всех наблюдений; 4) Сумму квадратов итогов по столбцам, деленных на число наблюдений в соответствующем столбце; 5) Квадрат общего итога, деленный на число наблюдений; 6) Отношение дисперсий. Если факторы А и В независимы. Каждое наблюдение служит одновременной оценкой обоих факторов и их взаимодействий. Какой анализ является необходимым и достаточным? Двухфакторный дисперсионный анализ Сколько отклонений от среднего значения, и сколько дисперсии вычисляется при двухфакторном дисперсионном анализе? четыре отклонения от среднего значения и три дисперсии. Дисперсионный анализ тесно связан с соответствующим планированием эксперимента. Если на результаты эксперимента действуют одновременно несколько факторов, то для анализа используется метод - … . латинские квадраты Для анализа с применением, какого метода необходимо, чтобы число уровней всех факторов было одинаковым, если нет, то этого можно всегда добиться, повторяя при эксперименте какие-либо из уровней недостающее число раз. метода латинские квадраты Схема расчета латинских квадратов, аналогична расчету при. двухфакторном дисперсионном анализе Когда определенное изменение в явлении причины приводит к строго определенному изменению в явлении следствия, то мы имеем … . функциональную связь Если при точно определенном изменении возраста не наблюдается строго определенного изменение артериального давления, то говорят о … . корреляционной связи Меру зависимости переменных определяет … .корреляция Если переменные измерены, как минимум, в интервальной шкале, то применяется Корреляция пирсона Коэффициенты корреляции изменяются в пределах от: от минус единицы до плюс единицы. Значения коэффициента корреляции -1.00 означает, что переменные имеют строгую ….отрицательную корреляцию Значение коэффициента корреляции +1.00 означает, что переменные имеют строгую ….положительную корреляцию Учитывая число наблюдаемых случаев можно установить, что если r = 0.00, то связь… .отсутствует Учитывая число наблюдаемых случаев можно установить, что если 0,3< r <0,5, то … связь выражена умеренно Корреляционная связь очень сильно выражена, если r>0,9. Корреляционная связь выражена слабо, если + 0,3< r <0,5. Корреляционная связь сильно выражена, если 0,7 < r < 0,9. Значение коэффициента корреляции не зависит … . от масштаба измерения. Прямую, построенную методом наименьших квадратов, называют … . прямой регрессии Коэффициент корреляции Пирсона (r) в квадрате представляет собой … . коэффициент детерминации. На практике линия регрессии чаще всего ищется в виде линейной функции. Это возможно с помощью метода … . наименьших квадратов Было проведено исследование о наличии взаимосвязи между двумя параметрами: возрастом (в годах) и площадью поражения артерий таза (в %) и построено уравнение регрессии. В данном случае площадь поражения артерий таза является: зависимой переменной; В уравнении регрессии ( 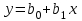 ) ) 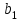 b1: коэффициентом регрессии; b1: коэффициентом регрессии;Если коэффициент корреляции равен 0, это означает связи между величинами нет;: Если коэффициент корреляции близок к 1, это означает связь между величинами сильная и прямая; Если коэффициент корреляции приблизительно равен 0,2, это означает связь между величинами слабая и прямая; Если зависимость между параметрами x и y прямо пропорциональная и функциональная, коэффициент корреляции между ними будет равен: r=1 В каких случаях для определения взаимосвязи между случайными величинами используется коэффициент корреляции Пирсона для определения линейной взаимосвязи В каких случаях для определения взаимосвязи между случайными величинами используется коэффициент корреляции Спирмена ранжированного ряда Если коэффициент корреляции равен -0,8, это означает связь между величинами сильная и обратная На каком отрезке лежат значения коэффициента корреляции (-1;1); В уравнении регрессии ( 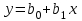 ) х является: независимой переменной; ) х является: независимой переменной;Если коэффициент корреляции близок к -1, это означает связь между величинами сильная и обратная Для вычисления коэффициентов в уравнении регрессии используется метод: наименьших квадратов Если коэффициент корреляции приблизительно равен -0,2, это означает связь между величинами слабая и обратная В уравнении регрессии ( 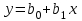 ) y является: зависимой переменной; ) y является: зависимой переменной;Регрессионный анализ позволяет: Дать количественную оценку взаимосвязи между признаками Под корреляцией понимается: Взаимосвязь между изучаемыми признаками Укажите методы расчета коэффициента корреляции: Метод квадратов (Пирсона) Цель исследования определяется на этапе: планирования и организации исследования Объект наблюдения, это: явление, подлежащее исследованию Единица наблюдения, это: отдельный случай изучаемого явления; Сплошное исследование: изучает все единицы, входящие в объект наблюдения Выборочное исследование: изучает часть единиц объекта наблюдения Число единиц наблюдения должно быть: оптимальным (не слишком малым, но и не неоправданно большим) Точность результата: приближение, с которым можно говорить о подлинности результата Научная гипотеза: предположение о сущности факта или ряда фактов Рандомизированное исследование, это: исследование со случайно отобранной контрольной группой При сравнении нескольких независимых групп с нормальным распределением признака нужно применять: дисперсионный анализ Линейная регрессия применяется: для вычисления прогнозных значений количественных признаков с нормальным распределением Связь между степенью тяжести послеоперационного осложнения и временем восстановительного периода в группе оперированных можно найти с помощью: корреляции Спирмена Коэффициент корреляции определяет степень связи признаков. Корреляционная связь признаков прямая, если с увеличением (уменьшением) значений одного признака, увеличиваются (уменьшаются) значения другого Корреляционная связь признаков обратная, если с уменьшением значений одного признака, увеличиваются значения другого Корреляция сильная, если коэффициент корреляции по модулю больше или равен 0,7 Корреляция слабая, если коэффициент корреляции близок к нулю, (по модулю меньше 0,3) Линейная корреляция Пирсона применяется для определения связи двух рядов количественных признаков с нормальным распределением Ранговая корреляция Спирмена используется для определения парных связей порядковых признаков Критерий Мак-Нимара применяется: для сравнения повторных измерений качественных признаков Какие из приведенных данных о послеоперационном больном являются полными, а не цензурированными: выздоровел Что не требуется в анализе выживаемости? чтобы все данные были полными, а не цензурируемыми Что является невозможным исследованием при анализе выживаемости: исследование зависимости уровня сахара от веса пациента Если коэффициент корреляции близок к 1, но р>0,05, это означает: связь между признаками сильная, но результат не является закономерным Однофакторный дисперсионный анализ (ANOVA) определяет значимость различия количественного признака с нормальным распределением в нескольких несвязных группах Что такое двойное слепое исследование? о том, какой препарат принимается, не знают ни пациенты, ни врач Проспективное исследование исследователь сам проводит наблюдение за пациентами, сбор и анализ данных. Продольные исследования продолжаются определенный период времени, когда принимается лечение и проводится наблюдение за пациентами Плотность населения – это относительная величина интенсивности Чему равен коэффициент корреляции двух независимых величин? r = 0 Критерий отношения дисперсий, F-критерий Фишера-Снедекора, используется для проверки … . гипотез о равенстве дисперсий в популяции Если смертность превышает рождаемость, то численность населения: убывает Какие данные называют цензурированными Наблюдения, которые содержат неполную информацию, Характеристика выживаемости это кривая выживаемости Выживаемость это вероятность пережить любой из моментов времени после некоторого начального события Какова доля выживших на первом году, если из 10 наблюдавшихся больных к концу первого года умер 1 человек 0,9 Какова доля выживших на втором году, если из 10 наблюдавшихся больных к концу первого года умер 1 человек, на втором году - умер 1 человек. 0,89 Какова функция выживания на первом году, если из 20 наблюдавшихся больных к концу первого года умерло 2 человека. 0,9 Какова функция выживания за два года, если из 10 наблюдавшихся больных к концу первого года умер 1 человек, на втором году - умер 1 человек.0,80 Из 10 наблюдавшихся после операции пациентов 2 человека за 2 года выбыли из наблюдения. Сколько цензурированных данных в выборке. 2 Как определяется выживаемость? отношение числа переживших момент t к общему числу наблюдаемых Что отражают данные выживаемости? время до достижения конечной точки + уровень смертности различных возрастных групп особей в популяции + вероятность пережить любой из моментов времени после некоторого начального события Кумулятивная доля выживших равно 0,672414 ,ширина интервала составляет 161 дней, в которой бльшая вероятность смертности. Какой показатель можно вычислить по этим данным и чему этот показатель равен? кумулятивная функция выживания равна 0.5. или 0,08 Метод анализа выживаемости: Метод Каплана Мейера Время, до которого доживет половина испытуемых, называется … выживаемости: медианой выживаемости Если вероятность наступления рецидива 0,1, то вероятность ненаступления рецидива:0,9 С целью проверки эффективности профилактического средства были отобраны 90 детей, склонных к простудным заболеваниям. Они были поделены на 3 равные группы случайным образом: контрольная, «плацебо» и «препарат». Единица измерения – время от окончания приема препарата до начала заболевания или выбывания.Какой из инструментов анализа выживаемости НАИБОЛЕЕ информативенпри установлении эффективности препарата? сравнение кривых выживаемости На протяжении двух месяцев осуществлялось наблюдение за 15 мужчинами старше 65 лет, перенесших инсульт. Начало каждого наблюдения –день возникновения инсульта. 10 наблюдений закончились смертью наблюдаемого, 4 пациента к концу исследования были живы и 1 выбыл.Какой из инструментов анализа выживаемости НАИБОЛЕЕ информативен в данном исследовании? кривая выживаемости При статистическом анализе клинического исследования с содержанием цензурированных данных был построен 95% доверительный интервал для каждого момента времени. Исследователь решил вместо 95% доверительного интервала просчитать 99% доверительный интервал.Какоеизменениедоверительного интервала НАИБОЛЕЕ вероятно? доверительный интервал станет шире На протяжении двух месяцев осуществлялось наблюдение за 15 мужчинами старше 65 лет, перенесших инсульт. Начало каждого наблюдения –день возникновения инсульта. 10 наблюдений закончились смертью наблюдаемого, 4 пациента к концу исследования были живы и 1 выбыл.Какое утверждение о медиане выживаемости НАИБОЛЕЕ вероятно, если будут известны моменты времени наступления каждого события? кривая выживаемости |
