ответф. +предметом, методологией, понятиями и категориями. предметом, методологией, понятиями и категориями
 Скачать 307.23 Kb. Скачать 307.23 Kb.
|
|
Статистика изучает: +массовые явления любой природы Чем отличается статистика от других наук: +предметом, методологией, понятиями и категориями. Статистическая совокупность – это: +любые изучаемые массовые явления Какими свойствами должна обладать статистическая совокупность: +множеством качественно однородных единиц, которым свойственны варьирующие признаки, подлежащие регистрации и изучению Статистическая методология включает: +методы сбора и систематизации данных, исчисления и анализа данных Статистическое исследование включает: +статистическое наблюдение, группировку и сводку, обработку и анализ данных Статистическое наблюдение – это: +научно организованный сбор данных о массовых явлениях и процессах по определенной программе По времени регистрации фактов наблюдение является: +периодическим Формами статистического наблюдения являются: отчетность и специальные статистические обследования Статистическая группировка – это: +объединение единиц совокупности в отдельные группы по внутренней однородности их и различиям между группами Дискретные группировочные признаки – это: + вариационные Дискретные признаки могут иметь: + только целые числовые значения Непрерывные признаки могут иметь: +любые значения в некотором интервале Интервал – это: +разность между верхней и нижней границами значений признака по одной группе Статистическая закономерность выявляется при изучении: + первичных массовых данных по изучаемому явлению Статистический расчет представляет собой: + исчисление статистических показателей Статистический показатель – это: +обобщающая характеристика какого-то свойства отдельных единиц, группы единиц или совокупности в целом Статистическая таблица – это: наглядное изложение (представление) в специальной (табличной) форме статистического материала Признак – это: +характеристика (качественная особенность) единицы совокупности Статистика изучает признаки, которые: +количественние и атрибутивные Количественные признаки могут быть представлены: + соответствующим размером и единицей измерения (численность населения, масса прибыли, средняя заработная плата) Атрибутивные признаки – это: +описательные Ряд (закон) распределения – это: + единицы совокупности, расположенные в порядке возрастания или убывания значений признака Полигон – это: + график дискретного ряда распределения Гистограмма – это: + график интервального ряда распределения Ряды распределения называются вариационными: + построенные по количественному признаку Под ранжированием понимают: + расположение всех значений в возрастающем (или убывающем) порядке Какой показатель в статистике называется абсолютной величиной: + показатель, который имеет физические единицы измерения Абсолютные статистические показатели выражаются: + в именованных числах Относительные величины – это: + отношение двух статистических величин Относительные статистические показатели выражаются: + в коэффициентах, промилле Средняя величина – это: + обобщенная типическая характеристика признака в данной совокупности Мода в ряду распределения – это: + значение признака, встречающееся чаще всего; Медиана в ряду распределения – это: +значение признака, делящее ряд распределения на две равные части; Вариация – это: + изменчивость (отклонение) индивидуальных значений признака по единицам совокупности Для измерения вариации значения признака применяются следующие статистические показатели: + размах вариации, среднее линейное отклонение, дисперсия, среднеквадратическое отклонение, коэффициент вариации Если все значения признака увеличить на некоторую постоянную величину, то средняя арифметическая: + увеличится на эту величину Если все значения признака умножить на некоторую постоянную величину, то средняя арифметическая: + увеличится во столько раз Если все значения признака увеличить на некоторую постоянную величину, то дисперсия: + не изменится Если все значения признака увеличить в 10 раз, то дисперсия: + увеличится в 10 раз Для сравнения вариации двух различных признаков необходимо использовать: + коэффициент вариации Если в ряду распределения частоты заменить частностями (удельными весами), то дисперсия: + не изменится Рядами динамики в статистике называются ряды показателей, характеризующих: изменения (развитие) явления во времени (ряд значений признака, соответствующих последовательности показателей времени) Средний уровень интервального ряда динамики определяется по формуле: + средней арифметической простой Статистический график – это: условное изображение статистических величин и их соотношений посредством линий, геометрических фигур, точек, рисунков или географических карт-схем Расчет каких ошибок наблюдения можно осуществить по математическим формулам: + случайных ошибок репрезентативности Ошибки репрезентативности возникают при: + не сплошном наблюдении В чем преимущества выборочного наблюдения перед сплошным: + экономия на материалах и денежных затратах При формировании выборочной совокупности соблюдение принципа случайности: +обязательно Как производится собственно случайный отбор: + абсолютно случайно или при помощи датчика случайных чисел; Как производится типический отбор: + Вся совокупность разбивается на типические группы по какому-либо существенному признаку, а затем из каждой группы осуществляется пропорциональный отбор случайным или механическим способом; Как определяются границы возможных значений генеральной средней: + Выборочная средняя плюс (минус) предельная ошибка выборочной средней; Статистическая гипотеза – это: +Предположение, которое можно проверить с использованием имеющейся статистической информации; Критерий – это: +Набор правил, принимаемых для проверки статистической гипотезы; Мощность критерия представляет собой: + Способность критерия четко различать нулевую и альтернативную статистические гипотезы; Ошибка первого рода – это: + отклонение статистической гипотезы, когда она правильна; Ошибка второго рода – это: + принятие статистической гипотезы, когда она ошибочна; Уровень значимости – это: +вероятность, соответствующая отклонению верной гипотезы; Величина, которая в результате испытания примет одно и только одно возможное значение неизвестное заранее. + Случайная Сумма произведений всех возможных значений величины на вероятности этих значений. + Математическое ожидание Такое значение случайной величины, что предшествующее и следующее за ним значения имеют вероятности, меньшие мода Таблица, в которой указаны возможные значения случайной величины и их вероятности. + Закон распределения Дан закон распределения дискретной случайной величины. Найти ее дисперсию.
+ 1,44 Дисперсия дискретной случайной величины равна 9, вычислить ее среднее квадратическое отклонение +3 Дан закон распределения дискретной случайной величины. Найти ее математическое ожидание.
0,15 Закон распределения дискретной случайной величины задан таблицей. Найти ее моду.
1 Найти математическое ожидание величины 122. 122 Среднее квадратическое отклонение дискретной случайной величины равно 3,1. Найти дисперсию этой величины. 9,61 Случайная величина, принимающая отдельные друг от друга возможные значения с определенными вероятностями, которые можно пронумеровать. дискретная Среднее квадратическое отклонение дискретной случайной величины равно 1,5. Найти дисперсию этой величины. 2,25 Коэффициент, который зависит от числа степеней свободы f и доверительной вероятности. коэф Стьюдента Интервальной оценкой математического ожидания является: доверительный интервал В математической статистике отношение суммы значений признаков к общему числу признаков: арифметическое среднее Среднее арифметическое квадратов отклонения значений признаков от их выборочной средней: дисперсия Случайная величина, принимающая все значения из некоторого конечного или бесконечного интервала: непрерывная Дисперсия постоянной D(C): равна 0 Квадратный корень из дисперсии среднее квадратическое отклонение Совокупность, состоящая из всех объектов, которые могут быть к ней отнесены. + генеральная Основоположник современной прикладной статистики и математической генетики. Рональд Фишер Число объектов, генеральной совокупности. Объем Наблюдаемые значения признака. Варианта Последовательность вариант, записанная в возрастающем (убывающем) порядке. Вариационный ряд, ранжированный ряд Сумма относительных частот выборки в математической статистике. равна единице Мера положения, которая является срединным значением упорядоченных наблюдений. Медианна Соответствие между возможными значениями случайной величины и их вероятностями. +Закон распределения случайных величин Законом распределения обычно называют … в которой случайные величины расположены в порядке возрастания или убывания. таблицу Оценка характеристик генеральной совокупности определяемая одним числом. Точечная Множество точечных оценок, определяемых числом наблюдений называют… . + Интервальной При исследованиях в фармации, медицине и биологии доверительную вероятность принимают равной... . +0,95% 0,05% При разработке стандартов доверительную вероятность принимают равной... . +0,99 При большом числе вариант, среднее считается надежным, если ошибка среднего ... t>3 Средняя масса таблетки при девятикратном измерении получилось 0,528 г. средняя квадратическая ошибка (0,014) и коэффициент Стьюдента (2,262) при надежности 0,95. Как записать окончательный результат измерений? 0,528+-0,014. Ошибка второго рода: Не отбрасывание нулевой гипотезы, когда она ложна Ошибка первого рода: Отбрасывание нулевой гипотезы, когда она верна Нулевая гипотеза ( 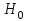 ): +Утверждение, которое не предполагает обнаружения влияния вмешательства в популяции ): +Утверждение, которое не предполагает обнаружения влияния вмешательства в популяции Частотное распределение: Показывает частоту появления каждого возможного наблюдения, класса наблюдений или категории Проверяет нулевую гипотезу, что среднее значение группы разностей парных наблюдений равна нулю Парный t критерий Критерий проверки гипотез, который не делает предположений о распределении анализируемых данных. Иногда называется критерий, свободный от распределения, или ранговый метод непараметрический критерий Исследует, отличается ли средняя переменной от некоторой гипотетической величины +Одновыборочный t-критерий (Стьюдента) Величина отдельной переменной, которая наиболее часто появляется в группе данных + Мода Доля пациентов с заболеванием, которые точно диагностированы тестом +чувствительность, специфичность теста 104. Число раз, когда происходит событие частота 105. Отдельная величина, полученная из исследования, которая оценивает параметр популяции +точечная оценка 106. Признак, который регистрируется для каждого из объектов, называют: +переменной 107. Значения переменных, которые регистрируются с помощью чисел, имеющих содержательный смысл, называют … данными + Количстсвенные 108. Переменная, которая может принимать значения только из некоторого списка определенных чисел. +дискретная 109. К какому типу переменных относится число детей в семье; число вызовов "скорой помощи", поступающих в больницу и т. п. + Дискретной 110. Непрерывной будем считать любую переменную, не являющуюся … +дискретной 111. Переменная, принимающая любые значения из некоторого промежутка. Непрерывная 112. Рост взрослого человека (например от 140 до 230 см), фактическая масса буханки хлеба (например от 750 до 830 г) и т.п. является примером … переменной. +Непрерывной 113. Данные, которые регистрируют определенное качество, которым обладает объект. +Качественные 114. Качественными называют данные регистрирующие … +определенное качество которым обладает объект 115. К полу человека приписываются соответственно числа 0 и 1. эти числа обрабатываются как … +качественные 116. Качественные данные, для которых нет содержательного смысла. +Номинальные 117. Качественные данные с содержательным смыслом +порядковые 118. Шкала, которая используется для регистрации самого низшего уровня измерений. номинальная 119. Шкала, в которой при измерениях на данном уровне практически не используются числа. Наименований 120. Шкала, для которой важно установить подобие или различие объектов по некоторому признаку +дело с качественными данными. Номинальная шкала 121. Шкала, используемая для распределения качественных данных. номинальная 122. Распределение по половому признаку, по месту жительства, по числу детей в семье являются примерами величин ….номинальной шкалы 123. Перечень объектов здравоохранения, занимающихся обслуживанием населения, охраной здоровья, диспансеризацией и пропагандой здорового образа жизни являются примерами величин … . номинальной шкалы 124. Шкала, указывающая лишь последовательность носителей признака или направление степени выраженности признака. Порядковая или ранговая шкала 125. Шкала, используемая для ранжирования по количеству правильно выполненных тестовых заданий. Порядковая 126. Шкала оценок по одной дисциплине является …, так как интервалы между отдельными баллами не отражают разрыва между реальными результатами. Номинальной шкалой 127. Шкала, отображающая одинаковую меру величины измеряемого признака является … . интервалов 128. Шкала, в которой расстояния между соседними делениями равны. интервалов 129. Величина главной тенденции в номинальной шкале является … . модальная величина, 130. Величина главной тенденции в порядковой шкале … .медиана 131. Величина главной тенденции в интервальной шкале является … среднее арифметическое. 132. Величина главной тенденции в пропорциональной шкале является … . средняя арифметическая, средняя геометрическая величина, установление тождества, кратности 133. Раздел вариационной статистики, с помощью методов которого производят обработку экспериментальных данных и наблюдений, а также планирование количественных экспериментов в биологических исследованиях. +Биометрия 134. Научная отрасль, связанная с разработкой и использованием статистических методов в научных исследованиях в медицине, здравоохранении, и эпидемиологии. +Биостатистика 135. Впервые ввел в употребление слово «biometry» и разработал основы корреляционного анализа. +Френсис Гальтон 136. Модой называется: + Варианта с наибольшей частотой 137. Медианой называется: +варианта находящаяся в середине ряда 138. Средняя арифметическая величина применяется для: +обобщения числовых значений варьирующего признака 139. Из всех видов распределения в медико-биологических исследованиях наиболее часто встречается: +нормальное 140. Основным условием применения параметрических методов анализа является: +нормальное распределение признака 141. Какое из приведенных ниже требований к выборочной совокупности является основным: +репрезентативность 142. Для большинства медико-биологических исследований оптимальной является вероятность безошибочного0 прогноза: +95,5 % 144. Главным свойством выборки является: +репрезентативность 145. Главным требованием к формированию выборки является: +случайность 146. Что такое малая выборка? + n меньше или равно 30 147. Под доверительным интервалом понимают: + пределы возможных колебаний показателя в генеральной совокупности 148. Величина доверительного коэффициента (t) определяется: Уровнем вероятности 149. Оценка достоверности полученного значения критерия t для малых выборок проводится по: +таблице Стьюдента 150. Эксцесс нормального распределения равен: +нулю 151. Знание статистических методов и правильный выбор статистических критериев позволяет сделать выводы … . + о степени надежности измерений 152. Под проверкой достоверности различий средних подразумевается проверка двух статистических гипотез, одна их которых называется …, а другая, конкурирующая с первой, называется … . + Нулевой, альтернативной 153. Уровень значимости – это +вероятность справедливости нулевой гипотезы при условии ее отвержения 154. Некоторые критерии могут применяться только в том случае, если известно, что переменные подчиняются конкретному закону распределения, например нормальному закону. Эти критерии называют: + Параметрическими 155. Основным фактором, часто ограничивающим применимость критериев, основанных на предположении нормальности, является: + объем или размер выборки, 156. Бесконечное множество значений, которые сплошь заполняют некоторый промежуток, соответствует: + непрерывной величине 157. Методы, называемые свободными от параметров или свободно распределенными. + непараметрические 158. Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке, то используете: + t-критерий для зависимых выборок 159. Обычно, когда имеются две выборки (например, мужчины и женщины), которые вы хотите сравнить относительно среднего значения некоторой изучаемой переменной, вы используете + t-критерий для независимых выборок 160. Непараметрический критерий, сравнивающий парные наблюдения +Критерий знаковых рангов Вилкоксона. 161. Нормально ли распределены данные позволяет определить …. +Критерий Колмогорова-Смирнова 162. Критерий проверки гипотез, который не делает предположений о распределении анализируемых данных. Иногда называется критерий, свободный от распределения, или ранговый метод +Непараметрический критерий 163. Качественные признаки нельзя изменить и единственной их количественной оценкой служит… +частота встречаемости 164. Качественные данные бывают двух типов: …, для которых существует имеющий содержательный смысл порядок, и …, для которых нет содержательно интерпретируемого порядка.+ порядковые, номинальные 165. Изучаются 2 группы. Значения изучаемых показателей: 2,3,4 и 5,6,7 соответственно. Найдите средние значения и дисперсии. +3,6 и 2,2; 166. Критерий проверки гипотез, который не делает предположений о распределении анализируемых данных. + Непараметрический критерий 167. Значение площади под кривой Гаусса, рассматриваемая для всего бесконечного промежутка (-бесконечность < x < +бесконечность), равна +1 168. Значение участка площади под кривой Гаусса, соответствующий промежутку от ‹ х › - δ < х < ‹ х › + δ. +0,683 169. Значение участка площади под кривой Гаусса, соответствующий промежутку от ‹х›-2δ до ‹х ›+2δ. +0,954 170. Значение участка площади под кривой Гаусса, соответствующий промежутку от ‹ х › – 3δ до ‹ х ›+3δ. +0,997 171. На практике можно полагать, что фактически все значения рассматриваемой случайной величины находятся в пределах промежутка, простирающегося + ‹х›–3σ до ‹ х›+3σ 172. Величина уровня значимости α, которая обычно применяется на практике +0,05 173. Статистические результаты, как правило: вероятностные 174. Нулевая гипотеза: + принимается в статистике в качестве рабочей гипотезы 175. Критический уровень значимости: + максимально приемлемая вероятность отвергнуть справедливую нулевую гипотезу 176. Если условия экспериментов неоднородны: +нельзя сравнить результаты, исходы 177. Количественный признак: + выражается и измеряется числовыми значениями 178. Качественный признак: + не может быть измерен количественно 179. Порядковый признак: + измеряется шкалой (ранжируется) 180. База данных: + таблица, содержащая единицы наблюдения и характеризующие их признаки 181. Статистика может: + дать статистическое оценивание результатов исследования 182. Статистика не может: + исправить ошибки в измерениях 183. Возможные проблемы статистической обработки: + некорректное использование статистических методов 184. Возможная статистическая ошибка: + использование неслучайных выборок 185. Основные описательные статистики количественного признака, это: + среднее, стандартное отклонение, ошибка среднего, процентили (нижний квантиль, медиана, верхний квантиль) 186. Распределение признака близко к нормальному, если среднее признака близко к медиане (различаются не более, чем на 20%) и в интервал "среднее плюс-минус стандартное отклонение попадает до 70% значений признака 187. Параметрические методы применяют только для анализа: + количественных признаков с нормальным распределением 188. Непараметрические методы применяют для анализа: + качественных, порядковых признаков и количественных, если распределение не является нормальным 189. Нормально ли распределение: 1, 1, 1, 1, 1, 1, 1, 1, 1, 5, 10, 10: + нет 190. Что значит «выявлены статистически значимые различия признака в группах сравнения»? +уровень значимости различия р<0,05 191. Можно ли применить критерий Стьюдента к сравнению признака «рост» с признаком «вес»? +нельзя 192. Формула критерия Стьюдента 193. Что характеризует стандартное (среднеквадратичное) отклонение? разброс значений количественного признака с нормальным распределением от среднего арифметического (ширину нормального распределения) 194. Какие характеристики хорошо описывают ассиметричное распределение? +квантилдер (персентилдер) 195. Чем не является дисперсия? + частотой признака 196. Нужно ли вычислять описательные статистики для качественных признаков? + нет, следует вычислить их частоты 197. Как выбрать статистический критерий для решения конкретной задачи? + по типу признака и виду исследования 198. Чем близки различные статистические критерии? + имеют сходный принцип действия: формулирование нулевой гипотезы, нахождение уровня значимости различия, сравнение его с критическим, вывод 199. Что выполняется раньше: проверка нормальности распределения количественного признака или критериальный анализ сравнения признаков в группах? + проверка нормальности распределения 200. Какой из критериев используется для проверки нормальности распределения? +Колмогоров-Смирнов Критерии стьюдента 201. Нулевая гипотеза. - предполагает, что различия значений признака в сравниваемых группах статистически незначимы, (или может быть принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями) 202. Различия признака в сравниваемых группах статистически значимы, если - вероятность ошибки отвергнуть справедливую нулевую гипотезу меньше 5% (р<0,05) 203. Если корректно примененный критерий не нашел статистически значимых различий (р>0,05): нужно проверить чувствительность критерия 204. Если чувствительность критерия низкая: нужно попытаться увеличить объем выборки, проанализировать выбросы 205. Что такое «нижний квартиль»? это 25-й персентиль: значение признака, которое делит распределение на 25% и 75%, четверть значений меньше нижнего квартиля, три четверти – больше 206. Что такое «верхний квартиль»? это 75-й персентиль: значение признака, которое делит распределение на 75% и 25%, т.е. три четверти значений меньше верхнего квартиля, четверть – больше 207. Что важнее в статистическом анализе? +корректно применять статистические критерии 208. Что не требуется при описании материалов исследования? семейное положение исследователя. 209. Что не является уровнем значимости различия (р)? ошибка второго рода 210. Что такое ошибка первого рода? вероятность найти различия там, где их на самом деле нет 211. Что такое ошибка второго рода? вероятность не найти различий там, где они есть 212. Под ранжированием понимают расположение всех значений в возрастающем (или убывающем) порядке. 213. Модой называется наиболее часто встречающееся значение признака в данном ряду 214. Общая дисперсия измеряет вариацию признака во всей совокупности 215. Предметом изучения статистики являются статистические: совокупности. 216. Исследование взаимосвязей варьирующих признаков в пределах однородной совокупности называется ... группировкой: аналитической 217. Если имеются следующие статистические данные: 10, 20, 30, 40, то дисперсия равна: 125 218. К требованиям в организации статистического наблюдения относятся: научность, массовость, планомерность 219. Если эксцесс …, то пик заострен, если …, то пик закруглен. – положительный, отрицательный 220. Основоположник современной прикладной статистики и математической генетики. Рональд Фишер 221. Разработчик теории выборочных распределений, методов дисперсионного и дискриминантного анализа, теории планирования экспериментов, метод максимального правдоподобия и многого другого. Фишер |
