Теоретические вопросы для подготовки к экзамену

• Название: Теоретические вопросы для подготовки к экзамену
• Дата: 06.01.2021
• Размер: 42.68 Kb.
• Имя файла: voprosy_ekzamen_MPOR_2020.docx
• Тип: Документы; #166140

Теоретические вопросы для подготовки к экзамену

1. 
   Особенности задач с целочисленными переменными.
   
2. 
   Основные понятия стохастических задач.
   
3. 
   Математические модели стохастических задач (стохастическое программирование).
   
4. 
   Особенности решения задач при случайной исходной информации.
   
5. 
   Общие понятия теории игр.
   
6. 
   Классификация игровых задач.
   
7. 
   Критерии выбора оптимальных стратегий: минимаксная группа критериев; статистические критерии.
   
8. 
   Постановка и классификация многокритериальных задач.
   
9. 
   Понятие Парето-оптимальных решений.
   
10. 
    Скаляризация векторного критерия.
    
11. 
    Виды и особенности сверток в многокритериальных задачах.
    
12. 
    Место и роль экспертных оценок в задачах принятия оптимальных решений.
    
13. 
    Ранговые оценки и согласованность мнений экспертов.
    
14. 
    Парные сравнения и модели их обработки.
    
15. 
    Метод анализа иерархий (метод Саати) в задачах многокритериальных решений.
    
16. 
    Примеры многокритериальных решений по методу Саати.
    
17. 
    Общие понятия о задачах оптимального управления.
    
18. 
    Принцип оптимальности Беллмана.
    
19. 
    Поиск оптимальных решений методом динамического программирования.
    

Примеры типовых практических заданий к экзамену.

1. 
   Практическое задание: Выполнить скаляризацию методом аддитивной свертки векторного критерия F(f1(x,y),f2(x,y),f3(x,y))→max, при условии, что f1(x,y)→max, f2(x,y)→min, f3(x,y)→min.
   

2. 
   Составить матрицу парных сравнений альтернатив при условии, что известны значения их критериальных показателей
   

А1 А2 А3 А4

К1 165 345 87 443

Критерий и шкалу предпочтений задать произвольно.

3. 
   Определите наилучшую стратегию принятия решения, используя критерии минимаксной группы.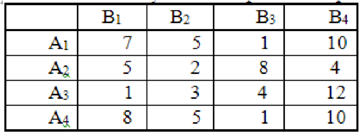
   

4. 
   Проверить матрицу парных сравнений на согласованность суждений ЛПР
   

К1→max А1 А2 А3 А4

А1 1 2 3 1/4

А2 1/2 1 1/3 1/2

А3 1/3 3 1 4

А4 4 2 1/4 1

5. 
   Произвольно задать для четырех альтернатив некоторые критериальные показатели, шкалу предпочтений и учитывая, что критерий→min построить матрицу парных сравнений.
   
6. 
   Определите наилучшую стратегию принятия решения, используя критерий Байеса-Лапласа (критерий максимального среднего выигрыша). Платежную матрицу задать произвольно.
   
7. 
   Матрица выигрышей в игре с природой имеет вид:
   

Найти оптимальное решение игрока, по критерию Гермейера.

	P(Q1)=0.7
	4	1
	3	3
	2	5
		6

8. 
   Пояснить механизм расчета
   

оптимального шагового управления и выигрыша (1 шаг управления)

Состояние

yA=fA[S1,xA(k)]+gB[S1–xA(k)]

Управление

Выигрыш

S1

xA(1)=0

xA(2)=1

xA(3)=3

k*A

x*A

gA(S1)

1

0+0=0

2+0=2

---

2

1

2

2

0+3=3

2+0=2

---

1

0

3

3

0+3=3

2+3=5

4+0=4

2

1

5

4

0+5=5

2+3=5

4+0=4

1 или 2

0 или 1

5

5

0+5=5

2+5=7

4+3=7

2 или 3

1 или 3

7

6

0+5=5

2+5=7

4+3=7

2 или 3

1 или 3

7

Состояние

yC=fC[S0, xC(k)]+gA[S1–xC(k)]

Управление

Выигрыш

S0

xC(1)=0

xC(2)=1

xC(3)=3

xC(4)=4

k*C

x*C

gC(S0)

6

0+7=7

2+7=9

3+5=8

5+3=8

2

1

9

9. 
   Изобразить граф оптимального управления при условии S0=6
   

Распределение оперативной памяти	Общий доход
xC(2)=1, xA(2)=1, xB(3)=4 xC(2)=1, xA(3)=3, xB(2)=2	yC(2)+xA(2)+xB(3)=2+2+5=9 yC(2)+xA(3)+xB(2)=2+4+3=9