МАИ_общее. 2. 4 Метод анализа иерархий
 Скачать 217.55 Kb. Скачать 217.55 Kb.
|
|
2.4 Метод анализа иерархий Самым эффективным методом принятия решений в сложных ситуациях является метод анализа иерархий (МАИ). Он был предложен американским ученым Т. Саати. Данный метод базируется на декомпозиции сложной проблемы, на ее более простые составляющие части и дальнейшей математической обработке последовательности суждений ЛПР, которые формируются в виде совокупности парных сравнений. В качестве преимуществ метода подчеркивалась способность данной модели разбивать сложную проблему на составляющие, облегчая при этом понимание самой цели. Также, необходимо отметить, что МАИ позволяет сравнивать качественные показатели с количественными. Такой подход обходит проблему разнородности факторов, влияющих на объект или ситуацию [5]. В качестве недостатков отмечается то, что требования к экспертам, расставляющим приоритеты, возрастает, это касается и образования, и опыта, а также умения эксперта работать с информацией, в том числе статистической. Еще одним недостатком является то, что при введении хотя бы одной новой альтернативы, отношение между существующими альтернативами меняется, в таком случае появляется необходимость повторных парных сравнений всего набора возможных вариантов. Иерархия формируется, начиная с вершины (цели), через промежуточные уровни (критерии или факторы, от которых зависят последующие уровни) к самому нижнему уровню (перечень альтернатив, из которых нужно осуществит выбор). Иерархию можно считать полной, в случае, когда каждый элемент верхнего уровня функционирует как критерий для всех элементов нижестоящего уровня. Рассмотрим две модификации данного алгоритма: анализ полной иерархической структуры; анализ иерархии с различным числом и составом альтернатив под критериями. Введем некоторые общие понятия. Пусть 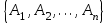 – множество n элементов некоторого уровня иерархии и – множество n элементов некоторого уровня иерархии и 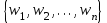 – абсолютные веса или интенсивности этих элементов, которые нам неизвестны заранее. Пусть для установления относительной важности элементов иерархии используется шкала отношений (таблица 1) [12]. – абсолютные веса или интенсивности этих элементов, которые нам неизвестны заранее. Пусть для установления относительной важности элементов иерархии используется шкала отношений (таблица 1) [12]. Таблица 1 – Шкала отношений (степени значимости действий)
Данная шкала позволяет ЛПР ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа. На основе выраженных численно результатов попарных сравнений потом решается задача по нахождению абсолютных весов. В идеале, при полной согласованности суждений матрица парных сравнений имеет вид (1).  (2.1) (2.1)Матрица 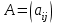 является квадратной и обладает свойством обратной симметричности (2). является квадратной и обладает свойством обратной симметричности (2).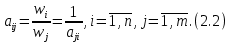 2.4.1. Алгоритм принятия решений для полной иерархической структуры (обобщенный алгоритм) Рассмотрим работу алгоритма принятия решения на примере (рисунок 2.3). 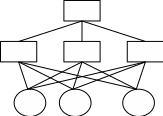 Рисунок 2.3 - Полная иерархическая структура Этап 1. Исходная задача представляется в виде иерархии, устанавливается взаимосвязь между множеством сравниваемых альтернатив 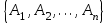 и множеством критериев и множеством критериев 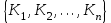 . .Этап 2. Установление приоритетов для критериев и оценка альтернатив. Формируется матрица попарных сравнений, с ее помощью сравнивается относительная важность критериев на втором уровне по отношению к обшей цели. Такие матрицы формируются для парных сравнений альтернатив по отношению к каждому из критериев второго уровня. Этап 3. После составления матриц попарных сравнений формируется набор локальных приоритетов, который получается в результате определения собственных векторов для каждой матрицы. Собственные векторы нормализуются, формируя вектор приоритетов. Для определения компонентов собственных векторов в МАИ используется оценки на основе среднее геометрического. Определим среднее геометрическое элементов строк полностью согласованной матрицы попарных сравнений 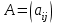 (3). (3).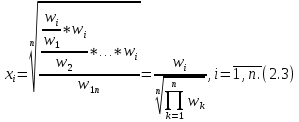 После нормализации вектора 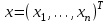 получаются компоненты вектора приоритетов (4). получаются компоненты вектора приоритетов (4).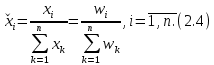 Умножим 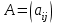 матрицу на вектор матрицу на вектор 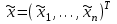 (5). (5).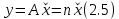 Приведенные соотношения (3) – (5) показывают, что при полной согласованности попарных суждений, выполняемые для матрицы 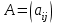 , проводимые вычисления восстанавливают истинные веса элементов по результатам попарных сравнений. Это помогает оценить степень их важности в целом. Полная согласованность попарных сравнений означает, что элементы матрицы , проводимые вычисления восстанавливают истинные веса элементов по результатам попарных сравнений. Это помогает оценить степень их важности в целом. Полная согласованность попарных сравнений означает, что элементы матрицы 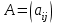 удовлетворяют уравнению (6). удовлетворяют уравнению (6).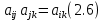 Однако получаемые на практике матрицы попарных сравнений не являются согласованными. Поэтому требуется оценить степень согласованности высказанных суждений. Полученные соотношения (3) – (5) определяют возможность подобной оценки степени согласованности суждений для любой обратносимметричной матрицы. Действительно, как следует из соотношения (5) для полностью согласованной матрицы 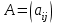 , величина , величина 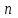 играет роль собственного числа, соответствующего собственному вектору играет роль собственного числа, соответствующего собственному вектору 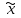 . В общем же случае для любой обратносимметричной матрицы . В общем же случае для любой обратносимметричной матрицы 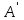 величина наибольшего собственного числа величина наибольшего собственного числа 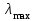 удовлетворяет неравенству (7). удовлетворяет неравенству (7).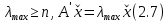 Поэтому величина ИС (8), 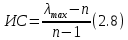 в МАИ применяется в качестве индекса согласованности. Кроме того, вводится отношение согласованности (9), 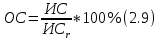 где 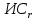 индекс согласованности, который получается при усреднении множества данных для матриц попарных сравнений при случайном равновероятном выборе количественных значений суждений из шкалы 1/10, 1/9,…, 9, 10, но с сохранением свойства обратной симметрии. индекс согласованности, который получается при усреднении множества данных для матриц попарных сравнений при случайном равновероятном выборе количественных значений суждений из шкалы 1/10, 1/9,…, 9, 10, но с сохранением свойства обратной симметрии.Значения 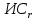 приведены в таблице 4. Величина OC считается приемлемой, если она имеет значения порядка 20% и менее. Если OC выходит из этих пределов, то можно рекомендовать лицам, формулирующим суждения, пересмотреть их с использованием дополнительной информации. приведены в таблице 4. Величина OC считается приемлемой, если она имеет значения порядка 20% и менее. Если OC выходит из этих пределов, то можно рекомендовать лицам, формулирующим суждения, пересмотреть их с использованием дополнительной информации. Таблица 2 – Индекс согласованности при случайной оценке сравнений
Этап 4. В конечном итоге для оценки степени согласованности реально получаемых в ходе опроса матриц попарных сравнений необходимо рассчитать ИС, ОС на основе определения величины 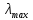 по следующим формулам (10) – (11), по следующим формулам (10) – (11),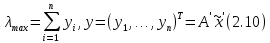 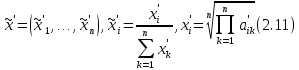 где 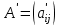 исследуемая матрица. Выражения (10), (11) по сути, повторяют цепочку выражений (3) – (5), проводимых для согласованной матрицы исследуемая матрица. Выражения (10), (11) по сути, повторяют цепочку выражений (3) – (5), проводимых для согласованной матрицы 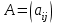 . .После того как получены достаточно согласованные оценки на различных уровнях и их локальные приоритеты, в МАИ осуществляется синтез глобальных приоритетов. Для этого по каждой i-ой альтернативе вычисляется величина (12), 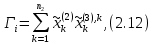 где 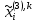 компонент вектора локальных приоритетов компонент вектора локальных приоритетов 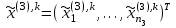 для i-ой альтернативы третьего (нижнего) уровня относительно i-го критерия верхнего уровня; для i-ой альтернативы третьего (нижнего) уровня относительно i-го критерия верхнего уровня; 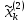 компонент вектора приоритетов компонент вектора приоритетов 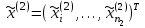 критериев второго уровня; критериев второго уровня; 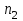 , , 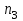 количество элементов, выделенных в иерархии на втором и третьем уровнях. количество элементов, выделенных в иерархии на втором и третьем уровнях. В остальных алгоритмах будем рассматривать только различия на втором этапе. 2.4.2. Выбор способа повышения привлекательности организации при помощи метода анализа иерархий Первым этапом метода анализа иерархий является построение самой иерархической модели, которая в упрощенном виде состоит из трех основных уровней: первый включает четко сформулированную цель, второй — критерии достижения цели, и третий представляет собой набор возможных альтернатив. Для того, чтобы получить максимально соответствующий цели результат, необходимо, в первую очередь, четко поставить цель. Общая цель принятия управленческого решения — это желаемое для ЛПР идеальное состояние объекта управления или проблемной ситуации. В нашем случае в качестве цели будет обозначена задача выбора, наиболее подходящего (менее затратного и эффективного) способа повышения привлекательности организации как места работы для привлечения новых сотрудников. Эта проблема рассматривается в менеджменте, маркетинге, связях с общественностью и подобных сферах деятельности. От того, насколько высоко себя позиционирует компания-работодатель, зависит стабильность кадрового показателя организации, что является немаловажным фактором ее коммерческой стабильности [15]. В ходе работы нами должны быть также рассмотрены несколько целевых аудиторий, на которых будут направлены те или иные действия организации, ведь именно в зависимости от этого, нами будут расставлены приоритеты критериев выбора альтернатив. В данной задаче необходимо учитывать интересы 3 групп при решении поставленной задачи. Так в первую очередь, необходимо учитывать желания сотрудников, уже работающих в данной организации. Вторая группа — группа, состоящая из возможных кандидатов на различные должности в организации. Третья группа состоит из руководителей компании, интересы которых необходимо учитывать для поддержки ими принятого в будущем решения. Главный эксперт, он же может быть и ЛПР, должен будет изначально расставить приоритеты именно этих групп в отношении друг друга. Это повлечет за собой более точную оценку важности тех приоритетов, которые уже будут расставлять выше перечисленные группы. Таким образом, мы попытаемся избежать усреднения оценок более важных и менее важных групп при решении конкретной задачи. Так как мы не вносим выше перечисленные расчёты в иерархию МАИ, то и высчитывать приоритетность можно вне метода. Поэтому мы расставили приоритеты с точки зрения основной цели компании, а именно повышение доходности предприятия. Исходя из этого, наибольший приоритет присвоен руководящим лицам, так как именно их финансовая и управленческая поддержка необходима при построении плана мероприятий. Учитывая тенденцию к сохранению кадров, на втором месте по приоритетности будет выступать группа сотрудников компании. Следовательно, наиболее меньший приоритет будет присвоен потенциальным сотрудникам. Выбор будет осуществляться среди 3 альтернатив, возможных вариантов способа достижения цели: улучшение условий труда (А). Данная альтернатива включает ремонт помещения и замену мебели; увеличение соцпакета и льгот (Б). Вариант включает также и предоставление абонементов в бассейн и спортзал, а также билетов в санатории; введение тренингов за счет компании (В). Альтернатива подразумевает введение бесплатных языковых или иных курсов в рабочее время; увеличение количества поощрительных мероприятий (Г). Предполагается введение оценки производительности работников по разным критериям и раз в квартал подводить итоги по отделам. Лучшим сотрудникам будет предложен вариант денежного вознаграждения. Далее необходимо определить критерии, то есть основания выбора альтернатив [2]: первоначальные затраты (K1); последующие затраты (K2); количество охватываемых сотрудников (K3); количество потенциальных сотрудников (K4); время внедрения (K5); окупаемость (K6). Они представлены уровнем выше. Таким образом, мы получили иерархическую модель нашей задачи (рисунок 2.4). 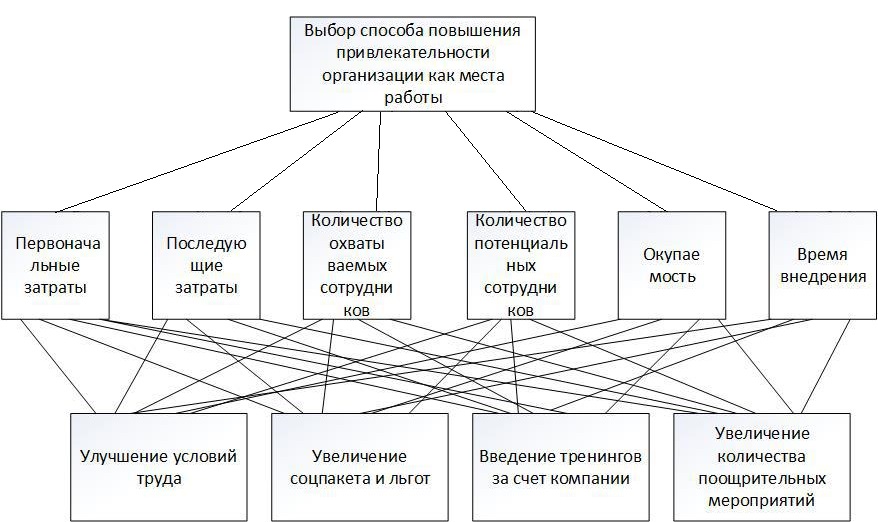 Рисунок 2.4 - Иерархическая модель задачи выбора способа повышения привлекательности организации как места работы Вторым этапом является процесс парных сравнений, который должен проводиться на каждом из уровней. Ниже приведены таблицы данных подсчетов для каждого уровня. В процессе парных сравнений нет необходимости в удержании в поле зрения всех рассматриваемых объектов, достаточно лишь работать с каждой из пар в отдельности – это еще одно из преимуществ МАИ. Перед тем, как эксперты начнут применять метод парных сравнений, главному эксперту будет необходимо, используя любой метод, расставить приоритеты групп экспертов. Данный подход позволит придать вес мнениям той группы, которая наиболее важна в рамках принятия решения в организации, касательно конкретной задачи [16]. В нашем случае наибольший интерес представляет группа людей, уже работающих в данной организации, но при этом, нельзя не заметить, что финансовую и управленческую поддержку будет обеспечивать группа руководящих лиц. В тоже время, направленность на потенциальных сотрудников, обязывает включить и их мнения в процесс принятия решения. Таким образом, наибольший приоритет был присвоен группе руководителей, а наименьший — группе потенциальных сотрудников. После работы самой экспертной группы, мы получим следующую таблицу.
Таблица 4 – Матрица парных сравнений для уровня 3.
Итак, мы получили иерархическую структуру и матрицы парных сравнений критериев и альтернатив по критериям. Для того чтобы определить насколько работа эксперта качественна, в методе Саати предусмотрены следующие показатели: ИС — индекс согласованности(13); ОС – отношение однородности(14). Таблица 5 – Индекс согласованности при случайной оценке сравнений
Показатель ИС не должна быть больше 10%, а ОС — больше 20%, в противном случае можно исключать подобные оценки экспертов из дальнейших расчетов. Это повышает качество работы, но не позволяет из группы экспертов вычислить того, который обладает большей компетенцией и опытом, чтобы контролировать согласованность суждений эксперта. Именно для этого было предложено оценить сами группы экспертов. 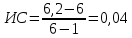 (2.13) (2.13)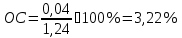 (2.14) (2.14)Анализируя полученные результаты, можно сделать вывод, что работа экспертов проведена качественно и соответствует стандартам МАИ, поэтому необходимо перейти к заключительному этапу работы с данным методом. Он заключается в расчете глобальных переменных, которые и определяют наиболее подходящую под нашу цель альтернативу. Для этого необходимо провести следующие расчеты для каждого из возможных вариантов (15): 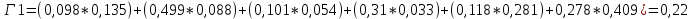 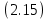 Таблица 6 – Расчет глобальных приоритетов
В данном примере, в качестве наилучшей альтернативы выступает введение тренингов за счет компании, что обусловлено малыми затратами и меньшим временем внедрения, именно эти критерии были выбраны руководящими лицами (наиболее важной, по мнению главного эксперта, группой) в качестве приоритетных. Таким образом, был проиллюстрирован метод анализа иерархий, который математическими расчетами обосновывает принятое решение. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
