Аналитическое решение. Предполагая, что ширина его бесконечна
 Скачать 57.94 Kb. Скачать 57.94 Kb.
|
|
Разработать программу численного моделирования процесса распространения электромагнитной волны в плоском однородном слое толщиной l, длиной L, предполагая, что ширина его бесконечна ly = . 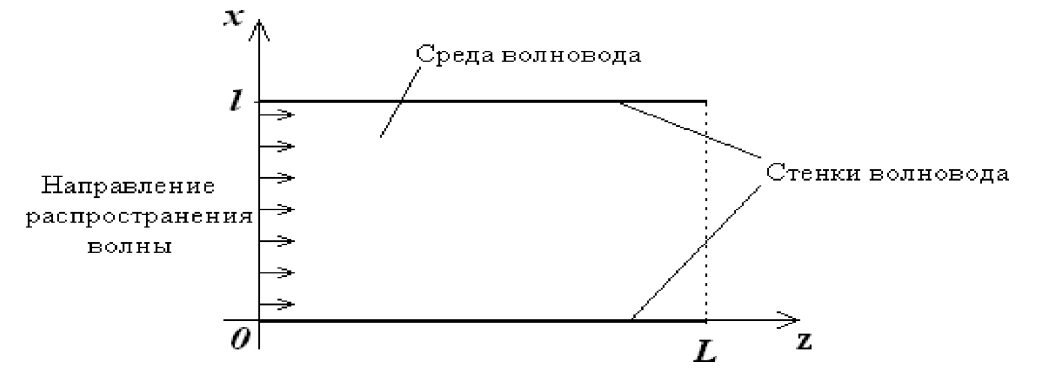 В нашем случае напряженность электрического поля 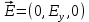 и магнитного поля и магнитного поля 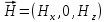 . Запишем краевую задачу для напряженности . Запишем краевую задачу для напряженности 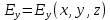 , предполагая, что в начальный момент времени t=0 при , предполагая, что в начальный момент времени t=0 при 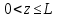 , , 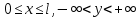 среда находилась в невозмущенном состоянии, а грань слоя x=0, x=l, z=Lвыполнены из электропроводящего материала. На грань z=0 при среда находилась в невозмущенном состоянии, а грань слоя x=0, x=l, z=Lвыполнены из электропроводящего материала. На грань z=0 при 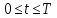 подается возмущающая электромагнитная волна с напряженностью подается возмущающая электромагнитная волна с напряженностью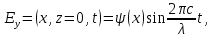 Где c – скорость распространения волны в среде, – длина возмущенной волны, 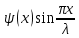 . .Спектр оператора Лапласа в классе 2π-периодических функций состоит из чисел 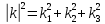 , которые равны квадратам длин целочисленных векторов k. Собственные функции , которые равны квадратам длин целочисленных векторов k. Собственные функции 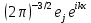 при при 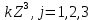 , образуют ортонормированный базис в пространстве , образуют ортонормированный базис в пространстве 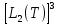 вектор-функций, интегрируемых с квадратом модуля в кубе Q. вектор-функций, интегрируемых с квадратом модуля в кубе Q. Любая вектор-функция 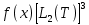 разлагается в ряд Фурье разлагается в ряд Фурье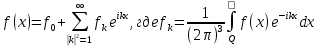 сходящийся в среднем квадратичном. Таким образом ряд Фурье в ортогональной системе выглядит следующим образом: 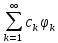 Где 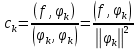 – коэффициенты Фурье. – коэффициенты Фурье.Электрическое поле гармонически зависит от времени t и удовлетворяет уравнениям Максвелла 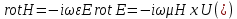 где Ex,y,z и Hx,y,z – комплексные амплитуды Диэлектрическая проницаемость внутри слоя описывается следующим законом: 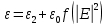 где fC0,h – произвольная функция (некоторые возможные ограничения на функцию f будут указаны далее); 2 max 1,3 – положительные константы. Будем искать решение уравнений Максвелла во всем пространстве. где =1, = 1, в U+ и =2, = 2, в U- краевым условиям 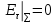 для касательных к поверхности идеального проводника. Рассмотрим ТЕ-поляризованные волны 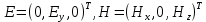 Предполагая, что компоненты поля гармонически зависят от z, 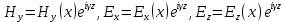 из (*) получаем систему уравнений из (*) получаем систему уравнений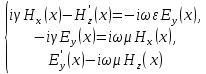 где – неизвестный спектральный параметр – постоянная распространения электромагнитной волны. После простейших преобразований из системы получаем 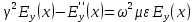 Введем обозначения k220, 0, и выполним нормировку в соответствии с формулами 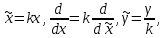 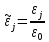 Компоненты полей f=Н1, Н2, Н3, Е1, Е1, Е3 удовлетворяют однородному уравнению Гельмгольца с параметром 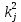 : :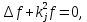 если 2>0 или 2>0, то для компонент u= Н1, Н2 или Е3 и ѵ = Е1, Е2 или H3 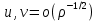 если 2=0, 2=0, 2>0 и 2>0, требуем, чтобы коэффициенты Фурье 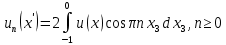 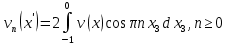 для компонент u= Н1, Н2 или Е3 и ѵ = Е1, Е2 или H3 удовлетворяли условиям 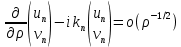 Основные уравнения (уравнения Максвелла) электродинамики в дифференциальной форме для произвольной временной зависимости и изотропной среды имеют вид 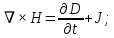 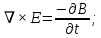 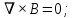 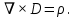 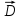 – вектор электрической индукции, – вектор электрической индукции, 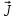 – вектор плотности электрического тока, – объёмная плотность электрических зарядов. – вектор плотности электрического тока, – объёмная плотность электрических зарядов.Внутренних источников нет j=0, тогда 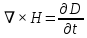 . .Материальные уравнения будут выглядеть следующим образом: 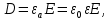 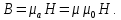 Где и 0 = 8,85410-12 – соответственно абсолютная и относительная диэлектрические проницаемости среды и вакуума; и 0 =410-7Гн/м –соответственно абсолютная, относительная магнитные проницаемости среды и вакуума. Распишем ротор как векторное произведение: 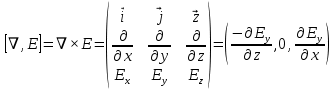 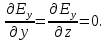 Последнее уравнение означает, что поле не изменяется вдоль осей y и z. 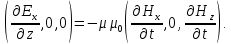 Аналогично 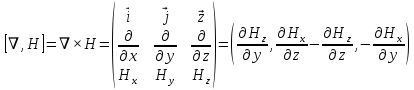 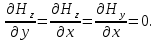 Тогда 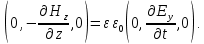 Расписываем скалярные уравнения, приравнивая соответствующие координаты: 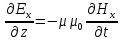 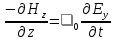 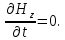 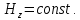 Производная по z: 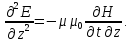 Теперь возьмем производную по t: 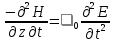 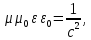 где 𝑐 – скорость распространения волны в среде. 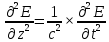 Получаем систему: 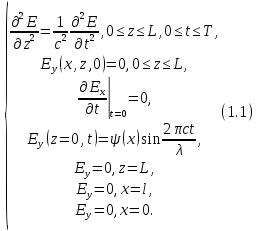 Подставим 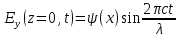 в во все условия системы (1.1) в во все условия системы (1.1)Полученная система является моделью описания процесса распространения плоской электромагнитной волны в полупространстве 𝑧 ≥ 0 на промежутке времени 0 < 𝑡 ≤ 𝑇. Найдем краевую задачу относительно u: 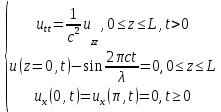 После подстановки 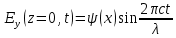 во все условия первой системы, сделаем замену переменных во все условия первой системы, сделаем замену переменных 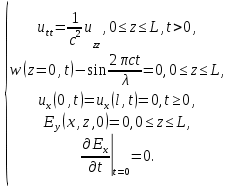 и применяя метод разделения переменных, т. е. находя решение вспомогательной задачи 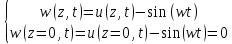 Решение задачи ищем в виде 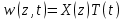 . .Получим задачу Штурма-Лиувилля для определения функции X(x). 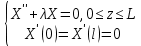 с решением 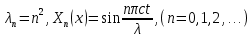 и уравнение и уравнение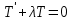 для определения T(t). Поскольку 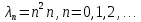 , то , то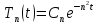 решение нашей задачи суть функции 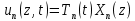 или 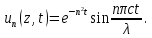 Поэтому решение исходной задачи дается рядом 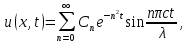 В нашем случае, учитывая начальное условие, получим (C2=1, Cn=0, n2) 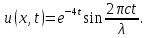 |
