Лр7. ЛР7 Карташов (2). Представление графа в эвм в виде матрицы смежности и списка ребер
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «СибирскИЙ государственнЫЙ Университет геоСИСТЕМ И ТЕХНОЛОГИЙ» (СГУГИТ)  ОТЧЕТ ЛАБОРАТОРНАЯ РАБОТА 7. ПРЕДСТАВЛЕНИЕ ГРАФА В ЭВМ В ВИДЕ МАТРИЦЫ СМЕЖНОСТИ И СПИСКА РЕБЕР Выполнил обучающийся группы БИ-12 Карташов Я.А. Проверила Ассистент кафедры ПИиИС Гришин Р.В. Новосибирск – 2022 Цель: получить практические навыки по представлению графа в памяти компьютера. Номер варианта – 5 Задание 1. Задан ориентированный граф. Необходимо на алгоритмическом языке написать две функции для объявления и заполнения матрицы смежности и матрицы инцидентности, описывающие граф. 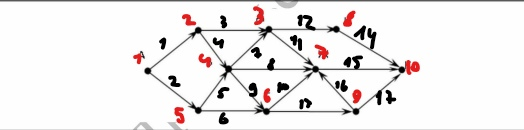 Матрица инцидентности:   Матрица смежности:   Задание 2. Получить у преподавателя персональную матрицу смежности графа. Количество вершин графа должно быть не менее 10, общее количество ребер 30, ориентированных ребер – не менее 18. Написать на алгоритмическом языке программу согласно своему варианту. 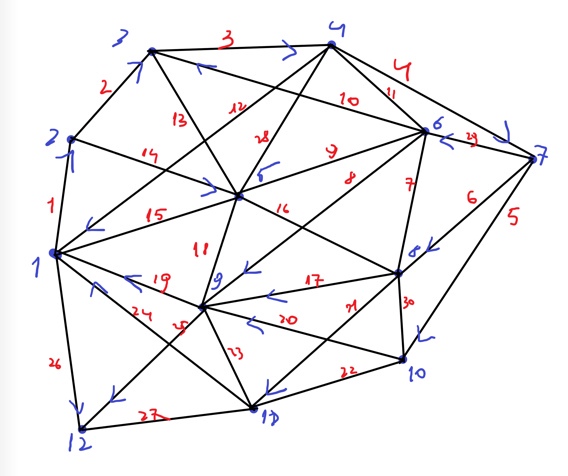
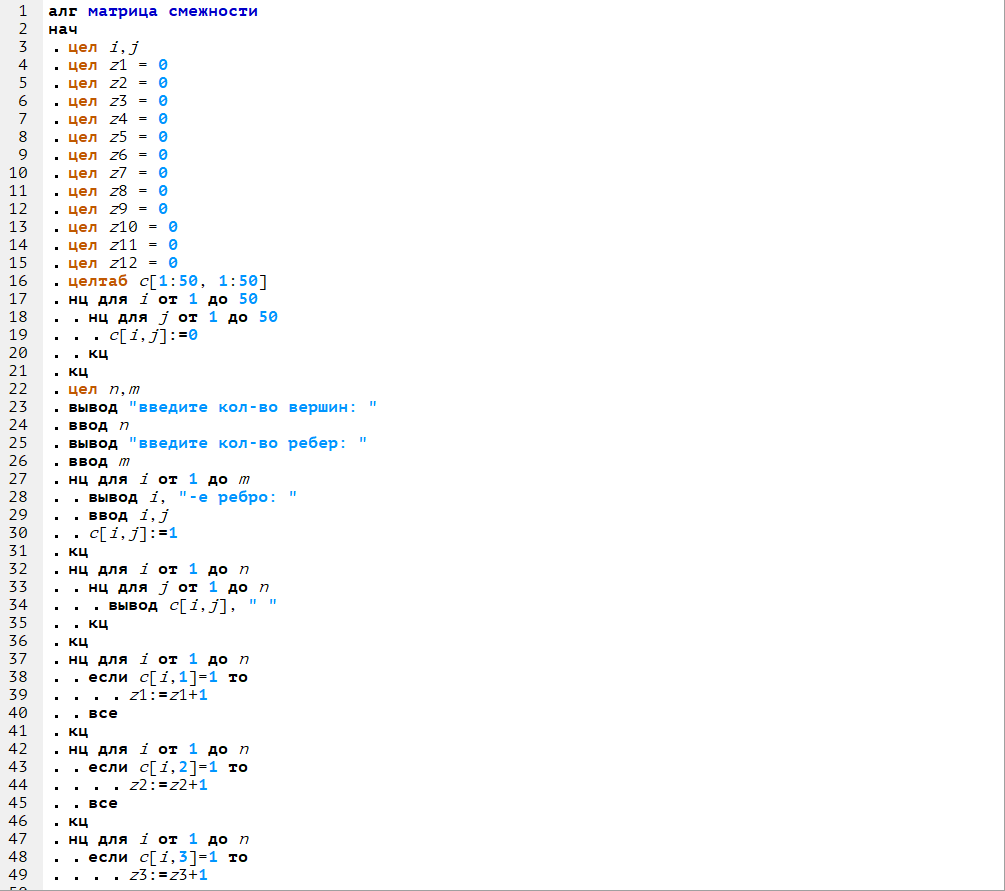    Ответы на контрольные вопросы: 1. Граф — математическая абстракция реальной системы любой природы, объекты которой обладают парными связями. Граф как математический объект есть совокупность двух множеств — множества самих объектов, называемого множеством вершин, и множества их парных связей, называемого множеством рёбер. 2. Ориентированные и неориентированные графы Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы Двудольный граф Эйлеров граф Регулярный граф Гамильтонов граф Взвешеный граф Графы-деревья 3. произвольное; прямолинейное — рёбра представляются отрезками; сеточное; полигональное — для отображения рёбер используются ломаные; ортогональное — рёбра представляются ломаными, отрезки которых — вертикальные или горизонтальные линии планарное; 4. Матрица смежности, матрица инцидентности. 5. Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова. 6. Остовное дерево может быть построено практически любым алгоритмом обхода графа, например поиском в глубину или поиском в ширину. Оно состоит из всех пар рёбер (u,v) таких, что алгоритм, просматривая вершину u, обнаруживает в её списке смежности новую, не обнаруженную ранее вершину v. Вывод: я получил практические навыки по представлению графа в памяти компьютера. |
