преобразование уравнений. Преобразование уравнений в равносильные данным. Решение рациональных, иррациональных, показательных, логарифмических уравнений
 Скачать 30.31 Kb. Скачать 30.31 Kb.
|
|
Преобразование уравнений в равносильные данным. Решение рациональных, иррациональных, показательных, логарифмических уравнений. Равносильные уравнения. Равносильные преобразования уравнений. Два уравнения с одной переменной  и и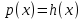 называются равносильными, если множества их корней совпадают, т.е. уравнения имеют одинаковые корни или не имеют корней. называются равносильными, если множества их корней совпадают, т.е. уравнения имеют одинаковые корни или не имеют корней.Например, 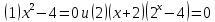  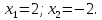  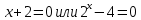 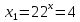 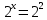 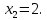 Уравнения (1) и (2) равносильны. 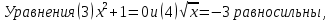 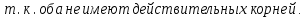 Замену одного уравнения другим равносильным ему уравнением называют равносильным преобразованием. Равносильные преобразования уравнений: Перенос слагаемых (с противоположным знаком) из одной части уравнения в другую. Умножение / деление обеих частей уравнения на число неравное нулю. Применение тождеств, т.е. равенств, справедливых для каждого 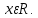 Возведение уравнения в нечетную степень. Замену уравнения 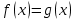 уравнением уравнением , называют возведением уравнения в степень n. , называют возведением уравнения в степень n.Например: Решим уравнение  Возведем обе части уравнения в 3-ю степень.  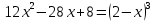 Применяем формулу куба разности в правой части уравнения, переносим все слагаемые с противоположным знаком из правой части в левую, приводим подобные слагаемые: 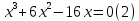    Уравнения (1) и (2) равносильны, поэтому корни уравнения (2) являются корнями уравнения (1). Ответ: 0; 2; -8. Извлечение корня нечетной степени из обеих частей уравнения. Замену уравнения 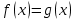 уравнением уравнением , называют извлечением корня степени n из обеих частей уравнения. , называют извлечением корня степени n из обеих частей уравнения.Например: Решим уравнение  Извлекаем корень 11-й степени из обеих частей уравнения:  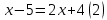  Уравнения (1) и (2) равносильны, поэтому корень уравнения (2) является корнем уравнения (1). Ответ: -9. Логарифмирование показательного уравнения. Замену уравнения 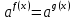 уравнением уравнением называют логарифмированием показательного уравнения. называют логарифмированием показательного уравнения.Решим уравнение 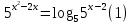 Прологарифмируем показательное уравнение по основанию 5: 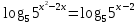 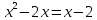   Уравнения (1) и (2) равносильны, поэтому корни уравнения (2) являются корнями уравнения (1). Ответ: 1; 2. Уравнения-следствия. Неравносильные преобразования уравнений Если каждый корень уравнения 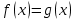 является в то же время корнем уравнения является в то же время корнем уравнения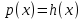 , то уравнение , то уравнение 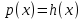 является следствием уравнения является следствием уравнения 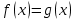 . .Например:  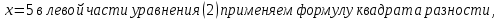  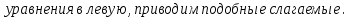 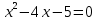 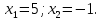 Корень уравнения (1) является одним из корней уравнения (2), значит уравнение (2) является следствием уравнения (1). Замену одного уравнения другим, которое является его следствием называется переходом к уравнению-следствию. При переходе к уравнению следствию возможна потеря корней и появление посторонних корней, поэтому необходимо в подобном случае выполнять проверку полученных корней. Преобразования, которые приводят к уравнению-следствию: Возведение обеих частей уравнения в четную степень. Например: Решим уравнение 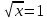 Возведем обе части уравнения в 4-ую степень: 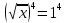 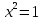  Выполнив проверку, т.е. подставив корни уравнения вместо х в исходное уравнения, получим, что х=-1 является посторонним корнем. Ответ: 1. Потенцирование логарифмического уравнения. Замену уравнения 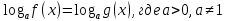 уравнением уравнением 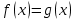 называют потенцированием логарифмического уравнения. называют потенцированием логарифмического уравнения.Например: Решим уравнение  Пропотенцируем логарифмическое уравнение по основанию 10:  Применяем основное логарифмическое тождество   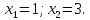 Выполнив проверку, т.е. подставив корни уравнения вместо х в исходное уравнения, получим, что х=1 является посторонним корнем. Ответ: 3. Освобождение от знаменателя Замену уравнения  уравнением уравнением  называют освобождением от знаменателя. называют освобождением от знаменателя.Например: Решим уравнение 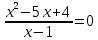   Выполнив проверку, т.е. подставив корни уравнения вместо х в исходное уравнения, получим, что х=1 является посторонним корнем. Ответ: 4. Применение формул (логарифмических, тригонометрических) Например: Решим уравнение  В левой части уравнения применяем свойство логарифмов, в правой части – представляем 3 в виде логарифма по основанию 2: 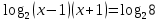 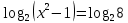    Выполнив проверку, т.е. подставив корни уравнения вместо х в исходное уравнения, получим, что х=-3 является посторонним корнем. Ответ: 3. Решите уравнения, указав какое преобразование применили:  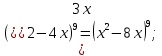   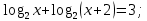 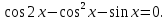 |
