|
Урок алгебры по теме Преобразования выражений, содержащих арифметические квадратные корни. У-66 ОУ. Преобразования выражений
Тема урока: Преобразования выражений,
содержащих арифметические квадратные корни
Тип урока: Урок обобщения и систематизации знаний
Формируемые результаты:
Предметные:формировать умение преобразовывать выражения, содержащие арифметические квадратные корни;
Личностные:формировать ответственное отношение к обучению, готовности к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
Метапредметные:формировать умение осуществлять контроль своей деятельности в процессе достижения результата;
Планируемые результаты: учащиеся научатся преобразовывать выражения, содержащие арифметические квадратные корни;
Основные понятия:арифметический квадратный корень,вынесение множителя из-под знака корня, внесение множителя под знак корня.
Формы работы: фронтальная (Ф), индивидуальная (И), групповая (Г)
Этапы проведения урока
|
Деятельность учителя
|
Деятельность
учащихся
|
1. Организационный этап
Мотивация учебной деятельности учащихся (создать благоприятную атмосферу на уроке, организовать начало учебной деятельности)
|
-Приветствует учащихся
- Древнегреческий поэт Нивей утверждал: «Математику нельзя изучать, наблюдая, как это делает сосед».
- Я желаю вам успешной самостоятельной работы на уроке и хорошего настроения!
- Каждый этап урока вы будете оценивать в оценочных листах
|
- Приветствуют учителя, включаются в деловой ритм урока
- Как вы понимаете эти слова?
- Ответы учащихся
- подписывают листы
|
2. Устный счет (И, Ф)
|
- Решение по тренажерам стр. 45 Г
- Тренировочные упражнения
|
- Выполняют вычисления по цепочке
- Ответы учащихся по желанию
Оценивание
|
3. Определение темы урока
|
- На слайде фотография, определить, что изображено.
Вопросы по данной фотографии:
- Как, данная фотография связана с нашим уроком?
|
-Ответы учащихся на уроке
|
4. Определение целей урока (Ф)
|
- Чем будем заниматься на уроке?
- Какие цели поставим?
|
- ответы учащихся
- формулируют цели урока
|
5.Актуализация знаний (Г)
(Проверка знаний теоретического материала)
|
Какие из следующих утверждений верные (неверные)?
|
- Выполняют задание, затем осуществляют проверку по слайду;
- Проговаривают правила неверных утверждений
Оценивание
|
6. Обобщение и систематизация знаний
(И, П)
|
2. Установите соответствие между выражениями;
|
Индивидуальная работа учащихся, затем взаимопроверка
Оценивание
|
7. ФКМ
|
Коллективное выполнение упражнений
|
8. Контроль и коррекция знаний (И)
|
Учащиеся выбирают уровень сложности самостоятельной работы и самостоятельно выполняют задания (тест), отмечая в тетрадях правильные ответ
|
- Выполняют решение с последующей самопроверкой
Оценивание
|
9. Подведение итогов (Г)
|
Учащиеся должны подготовить универсальную шпаргалку — опорный сигнал чтобы, посмотрев на нее, можно было найти ответы на все вопросы по данной теме
|
- Выполняют работу группой
|
10. Информация о домашнем задании
|
1. № 551, 568,570;
2. Составить кроссворд по данной теме
|
Записывают в дневник
|
11. Оценивание
|
Подводят итоги по оценочным листам (подсчитывают баллы и выставляют оценки)
|
Комментируют свою работу на уроке
|
12. Рефлексия учебной деятельности
|
Ответьте на вопросы:
- Какие виды деятельности на уроке были выполнены вами наиболее успешно?
- Назовите наиболее эффективные из них
- Заполните оценочную шкалу
|
Ответы учащихся по желанию
учащиеся приклеивают стикеры на шкалу
|
Какие из следующих утверждений верные?
Квадратным корнем из числа a называют число, квадрат которого равен а;
Арифметическим квадратным корнем из числа а называют отрицательное число, квадрат которого равен а;
Знак 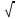 называют знаком квадратного корня или радикалом; называют знаком квадратного корня или радикалом;
Выражение, стоящее под знаком модуля, называют подкоренным выражением;
Подкоренное выражение может принимать только отрицательные значения;
Действие нахождения арифметического квадратного корня из числа называют извлечением квадратного корня;
Уравнение х2 = а при а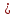 0 имеет один корень; 0 имеет один корень;
Уравнение х2 = а при а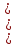 0 имеет два корней; 0 имеет два корней;
Уравнение х2 = а при а=0 не имеет корень;
Для любого действительного числа а выполняется равенство 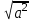 = =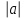 ; ;
Для любого действительного числа а и любого натурального числа n выполняется равенство 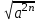 = =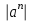 ; ;
Для любых действительных чисел a и b таких, что а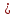 0 и b 0 и b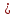 0, выполняется равенство 0, выполняется равенство
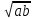 = =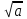 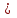 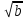 ; ;
Для любых действительных чисел a и b таких, что а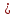 0 и b 0 и b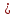 0, выполняется равенство 0, выполняется равенство 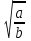 = =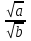 ; ;
Тождественные преобразования выражений, содержащих арифметические квадратные корни: вынесение множителя из-под знака корня, внесение множителя под знак корня, освобождение от иррациональности в знаменателе дроби.
________________________________________________________________________________
Какие из следующих утверждений неверные?
Квадратным корнем из числа a называют число, квадрат которого равен а;
Арифметическим квадратным корнем из числа а называют отрицательное число, квадрат которого равен а;
Знак 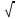 называют знаком квадратного корня или радикалом; называют знаком квадратного корня или радикалом;
Выражение, стоящее под знаком модуля, называют подкоренным выражением;
Подкоренное выражение может принимать только отрицательные значения;
Действие нахождения арифметического квадратного корня из числа называют извлечением квадратного корня;
Уравнение х2 = а при а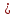 0 имеет один корень; 0 имеет один корень;
Уравнение х2 = а при а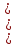 0 имеет два корня; 0 имеет два корня;
Уравнение х2 = а при а=0 не имеет корней;
Для любого действительного числа а выполняется равенство 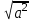 = =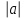 ; ;
Для любого действительного числа а и любого натурального числа n выполняется равенство 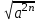 = =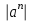 ; ;
Для любых действительных чисел a и b таких, что а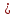 0 и b 0 и b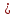 0, выполняется равенство 0, выполняется равенство
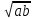 = =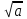 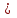 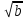 ; ;
Для любых действительных чисел a и b таких, что а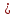 0 и b 0 и b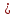 0, выполняется равенство 0, выполняется равенство 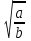 = =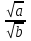 ; ;
Тождественные преобразования выражений, содержащих арифметические квадратные корни: вынесение множителя из-под знака корня, внесение множителя под знак корня, освобождение от иррациональности в знаменателе дроби.
Найдите значение выражения и расположите результаты в порядке возрастания
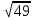 + + 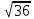 ; ;
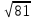 – – 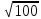 ; ;
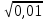 · · 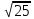 ; ;
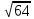 : : 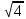 ; ;
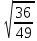 · · 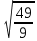 ; ;
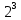 + 5 + 5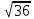 ; ;
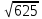 : : 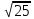 ; ;
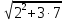 ; ;
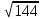 – – 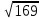 ; ;
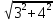 . .
|
Найдите значение выражения и расположите результаты в порядке убывания
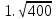 · · 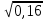 ; ;
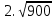 – – 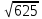 ; ;
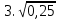 · · 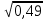 ; ;
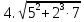 ; ;
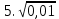 · ·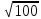 ; ;
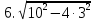 ; ;
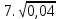 · · 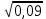 ; ;
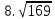 + + 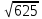 ; ;
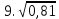 – – 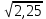 ; ;
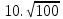 : : 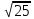 . .
|
Найдите значение выражения и расположите результаты в порядке возрастания
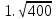 · · 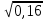 ; ;
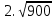 – – 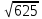 ; ;
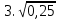 · · 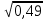 ; ;
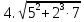 ; ;
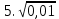 · ·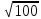 ; ;
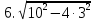 ; ;
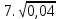 · · 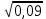 ; ;
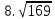 + + 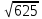 ; ;
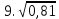 – – 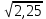 ; ;
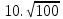 : : 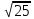 . .
|
Найдите значение выражения и расположите результаты в порядке убывания
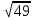 + + 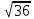 ; ;
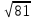 – – 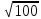 ; ;
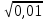 · · 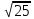 ; ;
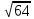 : : 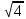 ; ;
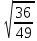 · · 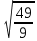 ; ;
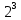 + 5 + 5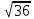 ; ;
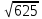 : : 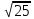 ; ;
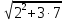 ; ;
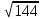 – – 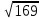 ; ;
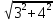 . .
|

Уровень 1
Оценка «3»
|
1.Какое выражение не имеет смысла?
А) 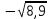 В) В) 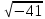 С) С) 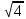 Д) Д)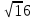
2.Найдите значение корня: - 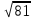
А) 18 В) - 9 С) 36 Д) 324
3.Вычислите 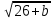 , если b=10 , если b=10
А) 216 В) 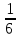 С) 12 Д) 6 С) 12 Д) 6
4.Решите уравнение 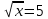
А) 25 В) - 25 С) 25; - 25 Д) не имеет корня
5.Найдите значение выражения: - 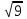 * * 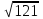
А) 22 В) 33 С) -33 Д) 0
|
Уровень 2
Оценка «4»
|
1.Найдите значение корня: 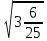
А) 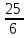 В) В) 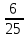 С) С) 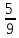 Д) Д) 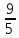
2.Найдите значение выражения: -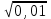 - - 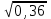
А) 0,5 В) -5 С) – 0,5 Д) – 0,7
3.Выполните действия x- 3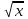 при х=9 при х=9
А) 0 В) 1 С) -1 Д) 0,5
4.При каких значениях у верно равенство 6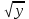 =6 =6
А) -1 В) 36 С) 1 Д) 0
5. Решите уравнение 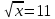
А) 121 В) - 121 С) 121; - 121 Д) не имеет корня
|
Уровень 3
Оценка «5»
|
1.Найдите значение выражения: 2 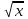 – х, при х=0,36 – х, при х=0,36
А) 7,2 В) -0,84 С) 0,84 Д) 0
2.Найдите значение корня: 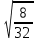
А) 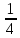 В) В) 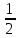 С) С) 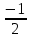 Д) нельзя извлечь Д) нельзя извлечь
3.При каком значении х верно равенство 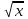 – 6 =0? – 6 =0?
A)1 B) 36 C) 6 Д) -6
4.Найдите значение выражения: 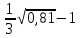
А) 0 В) 0,7 С) – 0,7 Д) - 3
5.При каких значениях х имеет смысл выражение 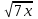 ? ?
А) при х>0 В) при х=0 С) при х< 0 Д) при х≥ 0
|
Уровень 1
Оценка «3»
|
В
В
Д
А
С
|
Уровень 2
Оценка «4»
|
Д
Д
А
С
А
|
Уровень 3
Оценка «5»
|
С
В
В
С
Д
|
|
Уровень 1
Оценка «3»
|
В
В
Д
А
С
|
Уровень 2
Оценка «4»
|
Д
Д
А
С
А
|
Уровень 3
Оценка «5»
|
С
В
В
С
Д
|
|
Уровень 1
Оценка «3»
|
В
В
Д
А
С
|
Уровень 2
Оценка «4»
|
Д
Д
А
С
А
|
Уровень 3
Оценка «5»
|
С
В
В
С
Д
|
|
Уровень 1
Оценка «3»
|
В
В
Д
А
С
|
Уровень 2
Оценка «4»
|
Д
Д
А
С
А
|
Уровень 3
Оценка «5»
|
С
В
В
С
Д
|
|
Фамилия
|
Имя
|
Задания
|
Количество баллов
|
Устный счёт
(максимальное количество баллов - 5)
МТ стр.45 Г
Тренировочные упражнения
|
|
Верные (неверные) утверждения
(за каждый правильный ответ 1 балл)
|
|
Установите соответствие
(за каждый правильный ответ 1 балл)
|
|
Самостоятельная работа
(разноуровневые задания)
Уровень 1: за каждый правильный ответ 1 балл
Уровень 2: за каждый правильный ответ 2 балла
Уровень 3: за каждый правильный ответ 3 балла
|
|
За активную работу в группе (2 балла)
|
|
Итоговое количество баллов
|
|
Оценка
|
|
Количество баллов 28 и более - оценка «5»
Количество баллов 22-27 - оценка «4»
Количество баллов 17-21 - оценка «3»
Количество баллов менее 17 оценка «2» - (надеюсь на отсутствие данной оценки)
Желаю успехов в работе!
|
|
Фамилия
|
Имя
|
Задания
|
Количество баллов
|
Устный счёт
(максимальное количество баллов - 5)
МТ стр.45 Г
Тренировочные упражнения
|
|
Верные (неверные) утверждения
(за каждый правильный ответ 1 балл)
|
|
Установите соответствие
(за каждый правильный ответ 1 балл)
|
|
Самостоятельная работа
(разноуровневые задания)
Уровень 1: за каждый правильный ответ 1 балл
Уровень 2: за каждый правильный ответ 2 балла
Уровень 3: за каждый правильный ответ 3 балла
|
|
За активную работу в группе (2 балла)
|
|
Итоговое количество баллов
|
|
Оценка
|
|
Количество баллов 28 и более - оценка «5»
Количество баллов 22-27 - оценка «4»
Количество баллов 17-21 - оценка «3»
Количество баллов менее 17 оценка «2» - (надеюсь на отсутствие данной оценки)
Желаю успехов в работе!
|
|
Установите соответствие:
|
1. (а – 4)(а + 4)
|
А. 5 – х2
|
2. (d - 7)(d + 7)
|
|
3. (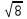 – b)( – b)(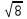 + b) + b)
|
Б. a² - 16
|
4. (5– х)(5 + х)
|
|
5. (d - 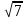 )(d + )(d + 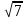 ) )
|
В. a - b
|
6. (а – 16)(а + 16)
|
|
7. (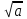 - - 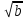 )2 )2
|
Г. d² - 7
|
8. (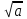 - - 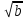 )( )(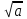 + +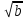 ) )
|
|
9. (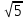 – х)( – х)(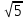 + х) + х)
|
Д. 8 - b²
|
10. (а - b)( а + b)
|
|
Установите соответствие:
|
1. (а – 4)(а + 4)
|
А. 5 – х2
|
2. (d - 7)(d + 7)
|
|
3. (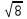 – b)( – b)(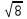 + b) + b)
|
Б. a² - 16
|
4. (5– х)(5 + х)
|
|
5. (d - 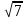 )(d + )(d + 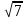 ) )
|
В. a - b
|
6. (а – 16)(а + 16)
|
|
7. (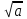 - - 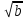 )2 )2
|
Г. d² - 7
|
8. (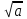 - - 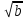 )( )(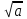 + +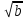 ) )
|
|
9. (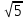 – х)( – х)(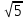 + х) + х)
|
Д. 8 - b²
|
10. (а - b)( а + b)
|
|
Установите соответствие:
|
1. (а – 4)(а + 4)
|
А. 5 – х2
|
2. (d - 7)(d + 7)
|
|
3. (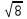 – b)( – b)(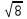 + b) + b)
|
Б. a² - 16
|
4. (5– х)(5 + х)
|
|
5. (d - 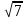 )(d + )(d + 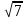 ) )
|
В. a - b
|
6. (а – 16)(а + 16)
|
|
7. (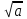 - - 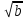 )2 )2
|
Г. d² - 7
|
8. (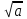 - - 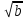 )( )(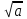 + +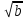 ) )
|
|
9. (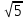 – х)( – х)(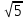 + х) + х)
|
Д. 8 - b²
|
10. (а - b)( а + b)
|
|
Установите соответствие:
|
1. (а – 4)(а + 4)
|
А. 5 – х2
|
2. (d - 7)(d + 7)
|
|
3. (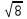 – b)( – b)(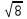 + b) + b)
|
Б. a² - 16
|
4. (5– х)(5 + х)
|
|
5. (d - 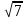 )(d + )(d + 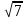 ) )
|
В. a - b
|
6. (а – 16)(а + 16)
|
|
7. (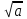 - - 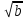 )2 )2
|
Г. d² - 7
|
8. (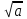 - - 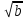 )( )(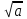 + +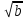 ) )
|
|
9. (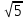 – х)( – х)(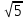 + х) + х)
|
Д. 8 - b²
|
10. (а - b)( а + b)
|
|
Одно из чисел 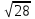 , , 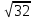 , , 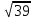 , , 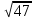 отмечено на прямой точкой A. Какое это число? отмечено на прямой точкой A. Какое это число?
А

5 6 7
Между какими числами заключено число 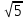 ? ?
2 и 3 3) 12 и 14
5 и 6 4) 26 и 28
Какое из данных чисел принадлежит промежутку 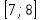 ? ?
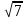 3) 3) 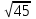
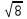 4) 4) 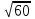
На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу 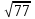 . Какая это точка? . Какая это точка?
A B C D
7 8 9
Какое из данных чисел 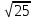 , , 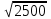 , , 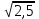 является иррациональным? является иррациональным?
|
|
|
 Скачать 235.67 Kb.
Скачать 235.67 Kb.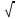 называют знаком квадратного корня или радикалом;
называют знаком квадратного корня или радикалом;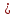 0 имеет один корень;
0 имеет один корень;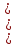 0 имеет два корней;
0 имеет два корней;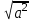 =
=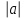 ;
;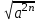 =
=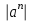 ;
;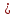 0 и b
0 и b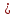 0, выполняется равенство
0, выполняется равенство 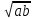 =
=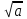
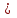
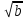 ;
;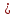 0 и b
0 и b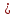 0, выполняется равенство
0, выполняется равенство 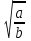 =
=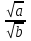 ;
;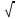 называют знаком квадратного корня или радикалом;
называют знаком квадратного корня или радикалом;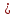 0 имеет один корень;
0 имеет один корень;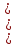 0 имеет два корня;
0 имеет два корня;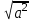 =
=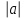 ;
;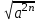 =
=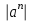 ;
;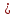 0 и b
0 и b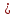 0, выполняется равенство
0, выполняется равенство 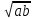 =
=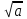
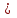
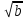 ;
;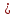 0 и b
0 и b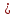 0, выполняется равенство
0, выполняется равенство 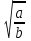 =
=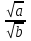 ;
;
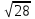 ,
, 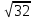 ,
, 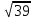 ,
, 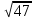 отмечено на прямой точкой A. Какое это число?
отмечено на прямой точкой A. Какое это число?
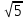 ?
?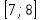 ?
?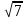 3)
3) 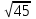
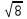 4)
4) 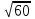
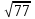 . Какая это точка?
. Какая это точка?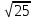 ,
, 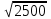 ,
, 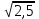 является иррациональным?
является иррациональным?
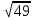 +
+ 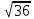 ;
;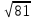 –
– 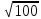 ;
;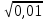 ·
· 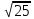 ;
;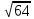 :
: 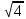 ;
;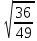 ·
· 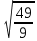 ;
;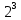 + 5
+ 5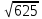 :
: 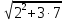 ;
;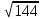 –
– 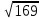 ;
;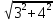 .
.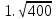 ·
· 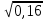 ;
;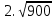 –
– 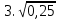 ·
· 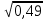 ;
;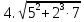 ;
;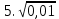 ·
·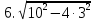 ;
;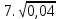 ·
· 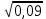 ;
;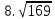 +
+ 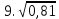 –
– 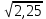 ;
;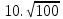 :
: 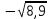 В)
В) 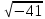 С)
С) 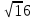
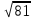
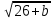 , если b=10
, если b=10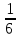 С) 12 Д) 6
С) 12 Д) 6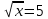
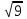 *
* 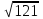
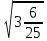
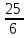 В)
В) 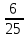 С)
С) 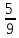 Д)
Д) 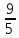
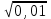 -
- 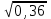
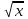 при х=9
при х=9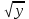 =6
=6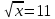
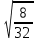
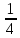 В)
В) 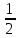 С)
С) 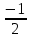 Д) нельзя извлечь
Д) нельзя извлечь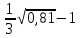
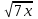 ?
?